3807
NUFFT: Fast Auto-Tuned GPU-Based Library1University of California, Berkeley, Berkeley, CA, United States, 2University of Göttingen, Göttingen, Germany
Synopsis
We present a fast auto-tuned library for computing non-uniform fast Fourier Transform (NUFFT) on GPU. The library includes forward and adjoint NUFFT using precomputation-free and fully-precomputed methods, as well as Toeplitz-based operation for computing forward and adjoint NUFFT in a single step. Computation of NUFFT depends heavily on gridding parameters, desired accuracy, trajectory type, amount of undersampling, and level of precomputation. The library automatically chooses optimal gridding parameters and algorithms, and it can be easily extended to include implementations from other libraries. The library allows researchers to accelerate iterative reconstructions without the difficulties of choosing optimal parameters and algorithms.
Purpose
With the emergence of iterative algorithms for reconstruction from undersampled data and the resurgence of non-Cartesian MRI, fast computation of the non-uniform fast Fourier Transform (NUFFT) is more important than ever. Here we show that the computation of NUFFT depends heavily on gridding parameters (grid oversampling ratio α and kernel width W), desired accuracy, trajectory type, amount of undersampling, and level of precomputation. These choices can lead to order-of-magnitude differences in computation of the same problem.
We present an auto-tuned library for computing NUFFT on GPU. Much like FFTW, it is based on separate planning and execution stages. Existing GPU-based libraries require the parameters α and W to be specified. Choosing these parameters can be difficult, as they affect both accuracy and runtime. Instead, the library automatically chooses α and calculates the corresponding W for a user-specified error level ε,1-2 defined as the maximum aliasing amplitude.3 Oversampling ratios are selected to produce grid sizes of the form 2a∙3b∙5c∙7d which are known to have fast FFT runtimes.
The library implements several algorithms, including adjoint
and forward NUFFT using precomputation-free and fully-precomputed methods. The
precomputation-free method is implemented as a direct convolution parallelized
across non-Cartesian samples with atomic operations for thread coordination,
whereas the fully-precomputed method performs convolution via sparse matrix-vector
multiplication. The library also includes a Toeplitz-based method for computing
forward and adjoint NUFFT in a single combined step,4 which can be
used in iterative reconstructions. The library is easily extended, and it can
include other implementations such as gpuNUFFT,5 which uses partial
precomputation and load-balancing, where non-Cartesian samples are grouped into
spatial sectors. Through planning, the
library can choose algorithms and parameters that will optimize the runtime.
Methods
We compare our library to existing GPU-based libraries, gpuNUFFT and PowerGrid,6 on a Tesla K40 GPU. We also compare to a serial CPU-based implementation from the BART library.7
We benchmarked total time for forward and adjoint operations on 3D problems with reconstruction size N3, where N = 62, 94, 126, 154, 190, 222, 254; radial, stack-of-stars, cones,8 and uniformly random trajectories; levels of undersampling R = 1, 4, 16; and error levels ε = 0.01, 0.001. Each measurement is taken from the median time of 100 executions, without CPU-GPU memory transfer times.
Results and Discussion
Results show that auto-tuning improves performance. Speedups are lower when α is fixed, compared to speedups when we tune for αoptimal (Fig. 1).
Fig. 2-3 show speedups over BART NUFFT for various implementations, with ε = 0.01 and ε = 0.001. The fully-precomputed method attains high speedups overall. Precomputation is beneficial at higher accuracy levels, where W is high and other methods need to enumerate many grid points on-the-fly. However, the fully-precomputed method requires much more memory than other methods. This method is suitable for high levels of undersampling, where it achieves high speedups and the required memory is low.
gpuNUFFT performs well on trajectories with uneven distribution of samples (i.e. radial), where load-balancing is crucial to performance. gpuNUFFT also performs well for moderate accuracy levels and levels of undersampling. At high accuracy levels, gpuNUFFT requires more shared memory due to increased kernel width, which limits GPU occupancy. Additionally, synchronization is required for writing to shared and global memory, creating overhead that may be less suitable to highly undersampled trajectories.
The precomputation-free method can be used in all other situations for high levels of accuracy or undersampling, limited memory usage, or when load-balancing is unnecessary.
The Toeplitz method achieves the highest speedups for high accuracy levels and fully sampled trajectories. Unlike gridding-based methods, the runtime for Toeplitz method is independent of ε, as only a change in the computed PSF is required during the planning stage.
PowerGrid achieves lower speedups than other libraries by an order of magnitude. Since its performance is not currently competitive with other implementations, we will not discuss it further here.
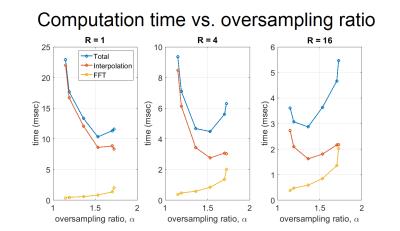
Fig. 4 shows the oversampling ratios αoptimal chosen by auto-tuning. αoptimal decreases with increased undersampling because interpolation time decreases and the runtime is more evenly distributed between interpolation and FFT (Fig. 5). The decrease in αoptimal is less pronounced at higher accuracy levels, since interpolation time is longer relative to FFT time due to correspondingly higher kernel widths. These observations can be used to design further heuristics for choosing α based on ε and R.
Conclusion
Through planning stages and heuristics, our auto-tuned NUFFT library allows researchers to accelerate iterative image reconstructions, without the burden of choosing gridding algorithms and parameters that affect runtime on different GPU architectures in unpredictable ways.Acknowledgements
We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Tesla K40 GPU used for this research.References
1. Murphy, Mark. "Parallelism, patterns, and performance in iterative MRI reconstruction." PhD diss., University of California, Berkeley, 2011.
2. Murphy, Mark, Michael Zarrouk, Kurt Keutzer, and Michael Lustig. “nuFFTW: A Parallel Auto-Tuning Library for Performance Optimization of the nuFFT.” In Proc Intl. Soc. Mag. Res. Med. 2013.
3. Beatty, Philip J., Dwight G. Nishimura, and John M. Pauly. "Rapid gridding reconstruction with a minimal oversampling ratio." IEEE transactions on medical imaging 24, no. 6 (2005): 799-808.
4. Wajer, F. T. A. W., and K. P. Pruessmann. "Major speedup of reconstruction for sensitivity encoding with arbitrary trajectories." In Proc. Intl. Soc. Mag. Res. Med, p. 767. 2001.
5. Knoll, F., A. Schwarzl, C. Diwoky, and D. K. Sodickson. "gpuNUFFT-An Open Source GPU Library for 3D Regridding with Direct MATLAB Interface." In Proceedings of the 22nd Annual Meeting of ISMRM, Milan, Italy, p. 4297. 2014.
6. Cerjanic, Alex, Joseph L. Holtrop, Giang Chau Ngo, Brent Leback, Galen Arnold, Mark Van Moer, Genevieve LaBelle, Jeffrey A. Fessler, and Bradley P. Sutton. "PowerGrid: A open source library for accelerated iterative magnetic resonance image reconstruction." In Proc. Intl. Soc. Mag. Reson. Med. 2016.
7. Uecker, Martin, Frank Ong, Jonathan I. Tamir, Dara Bahri, Patrick Virtue, Joseph Y. Cheng, Tao Zhang, and Michael Lustig. "Berkeley advanced reconstruction toolbox." In Proc. Intl. Soc. Mag. Reson. Med, vol. 23, p. 2486. 2015.
8. Gurney, Paul T., Brian A. Hargreaves, and Dwight G. Nishimura. "Design and analysis of a practical 3D cones trajectory." Magnetic resonance in medicine 55, no. 3 (2006): 575-582.
Figures
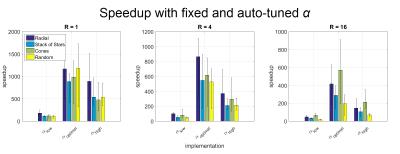
Figure 1. Speedup over BART NUFFT (serial CPU implementation) for gpuNUFFT, with and without auto-tuning (fixed α and tuned αoptimal).
Auto-tuning strongly impacts NUFFT runtime. Speedups are much higher when using auto-tuned αoptimal, than when using a fixed α (αlow = 1.125, αhigh = 2). (Error level ε = 0.01, with factors of undersampling R = 1, 4, 16. Speedup is averaged across different problem sizes. Error bars show minimum and maximum speedup.)
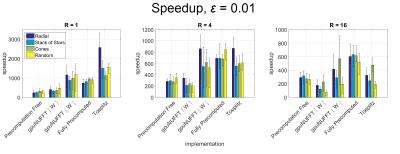
Figure 2. Speedup over BART NUFFT (serial CPU implementation) for various GPU implementations of forward and adjoint NUFFT, averaged across different problem sizes. Error level ε = 0.01, with factors of undersampling R = 1, 4, 16.
Fully precomputed method achieves high speedups, but uses much more memory than other methods. gpuNUFFT achieves comparable speedups, while using much less memory. gpuNUFFT performs especially well for the radial trajectory due to load balancing. (gpuNUFFT was benchmarked with sector size 83 and with W rounded both up and down, since gpuNUFFT allows integral W values only.)
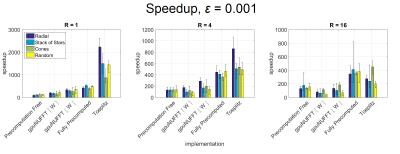
Figure 3. Speedup over BART NUFFT (serial CPU implementation) for various GPU NUFFT implementations of forward and adjoint NUFFT, averaged across different problem sizes. Error level ε = 0.001, with factors of undersampling R = 1, 4, 16.
Toeplitz method achieves high speedups at high accuracy levels, since its runtime is independent of ε. Fully precomputed method also achieves high speedups at this error level, whereas performance of gpuNUFFT is limited by its shared memory usage.
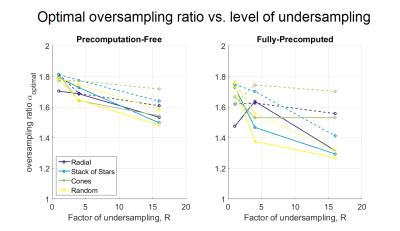
Figure 4. Average optimal oversampling ratios αoptimal selected via auto-tuning, vs. level of undersampling R = 1, 4, 16. Accuracy levels ε = 0.01 (solid lines) and ε = 0.001 (dashed lines).
As R increases, αoptimal decreases because the interpolation time decreases and FFT time starts to become a larger fraction of total runtime. The change in αoptimal is larger for the fully-precomputed method than precomputation-free approach, since interpolation requires less time for the fully-precomputed method. For the same reason, the change in αoptimal is larger at ε = 0.01 than at ε = 0.001.