3800

Quantification of cerebral venous oxygenation using a two-compartment model of local phase evolution

Elena Kleban¹, Richard Bowtell¹, Penny Gowland¹, and Molly Bright¹

¹Sir Peter Mansfield Imaging Centre, University of Nottingham, UK, Nottingham, United Kingdom

Synopsis

We propose that a two-compartment model of the evolution of signal phase, processed using Frequency Difference Mapping, could be applied to study venous oxygenation and architecture at the microscopic scale. This study demonstrates proof-of-concept, quantifying Yv in large vessels, and tests the sensitivity of these values to hyperoxia. We discuss how this new method can be adapted to probe venous microstructure within grey matter, providing more sensitive measures of brain tissue function.

Purpose

MRI methods to quantify cerebral venous oxygenation, $$$Y_\text{v}$$$, offer an exciting biomarker for tissue metabolism. Existing techniques characterise intra-vascular magnitude or phase information to measure $$$Y_\text{v}$$$, however these are limited to studying vessels larger than the imaging resolution^1,2. Smaller vessels with known geometry can be examined, modelling the gradient-echo signal decay as a two-compartment model containing tissue and venous contributions³. An alternative approach⁴ induces a change in perivascular signal phase by altering blood oxygen levels, removing dependence on vessel geometry, however this is also only appropriate for single, resolved veins.

We propose that a two-compartment model of the evolution of signal phase, processed using Frequency Difference Mapping⁵, could be applied to study venous oxygenation and architecture at the microscopic scale. This study demonstrates proof-of-concept, quantifying $$$Y_\text{v}$$$ in large vessels, and tests the sensitivity of these values to hyperoxia. We discuss how this new method can be adapted to probe venous microstructure within grey matter, providing more sensitive measures of brain tissue function.

Methods

Data Acquisition

Multi-echo gradient-echo 2D sagittal single-slice magnitude and phase images were acquired from 4 healthy volunteers on a 7T Philips Achieva (Netherlands), scanning parameters are listed in Table 1. For one participant, normoxic/hyperoxic gas mixtures were delivered using the RespirAct^TM system (TRI, Canada) to modulate $$$Y_\text{v}$$$; this data was acquired during short breath-holds to reduce respiration-related phase artifacts, and 10 acquisitions for each gas mixture were averaged.

Two-compartment model

The complex signal evolution with echo-time $$$\text{TE}_n=\text{TE}_1+(n-1)\Delta\text{TE}$$$ from a voxel can be described using a 2-compartment model

$$$S_n=S(\mathrm{TE}_n)\sim{}S_\text{venous}+S_\text{tissue}=\lambda\cdot{}e^{-R^*_{2,\text{t}}\text{TE}_n}+(1-\lambda)\cdot e^{-R^*_{2,\text{v}}\text{TE}_n}\cdot{}e^{i\langle\Delta\omega\rangle\text{TE}_n},\qquad\qquad\qquad\qquad\qquad[1]$$$

where $$$R_2^*$$$ denotes the venous and tissue rates of relaxation, $$$\lambda$$$ is the venous signal fraction and $$$\langle\Delta\omega\rangle$$$ is the average orientation- and oxygenation-dependent frequency offset:

$$$\langle\Delta\omega\rangle=\frac{1}{2}\cdot\gamma{}B_0\cdot\Delta\chi_\text{do}\cdot\text{hct}\cdot(1-Y)\cdot\left(\cos^2\theta-\frac{1}{3}\right).\qquad\qquad\qquad\qquad\qquad[2]$$$

Fitting the 2-compartment model, assuming hct=0.45 and $$$\Delta\chi_\text{do}=4\pi\cdot0.18{}$$$ppm, and estimating the orientation of each vessel from the ROI geometry, we can then calculate $$$Y_\text{v}$$$ from the FDM results.

FDM analysis of signal phase

Prior to modelling the signal, the complex data were pre-processed by removing the RF-related phase offsets and large length-scale field variations. This can be established as described previously5, calculating the frequency difference map (FDM) at each TE as:

$$$\text{FDM}(\text{TE}_n)=\arg\left(\frac{S_n\cdot S_1^{n-2}}{S_2^{ni1}}\right)\cdot\frac{1}{s\pi\cdot(\text{TE}_n-\text{TE}_1)}\qquad\qquad\qquad\qquad\qquad[3]$$$

Large veins were identified in the magnitude images at $$$TE=20\,$$$ms ; ROIs were drawn around straight segments of each vessel, and the vessel orientation with respect to $$$\vec{B}_0$$$ represented by angle was estimated. Frequency difference and magnitude data were averaged across each ROI for each echo.

Results

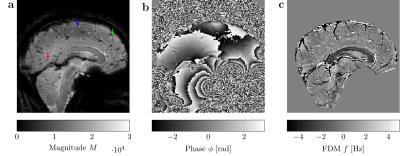
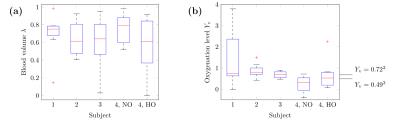
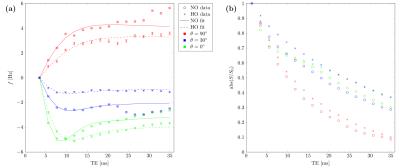
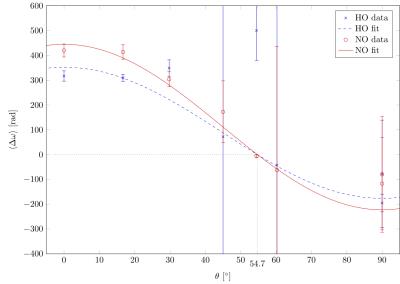
Figure 1 provides example magnitude, phase and calculated FDM images. The distributions of $$$\lambda$$$ and $$$Y_\text{v}$$$ values estimated from the best-fitting parameters for 8 vessels from each scan are presented in Figure2. To examine the sensitivity of these results to changes in orientation and oxygenation, the normoxia/hyperoxia magnitude and FDM data in 3 vessels of different orientations, and the 2-compartment model fits to these data, are presented in Figure3. Fitted values for $$$\langle\Delta\omega\rangle$$$ from all 8 ROIs in these scans are plotted as a function of (Figure4), and fit using Eq.2 to measure $$$Y_\text{v}(\text{normoxia})=0.30\pm0.05$$$ and $$$Y_\text{v}(\text{hyperoxia})=0.45\pm0.07$$$.

Discussion

Quantification of $$$Y_\text{v}$$$ Several vessel ROIs produced non-physiological $$$Y_\text{v}$$$ values above 1, as well as implausible blood volume measurements. Figure 4 shows that inaccurate fitting of $$$\langle\Delta\omega\rangle$$$ occurs when $$$\theta$$$ approaches the magic angle, which reflects a fundamental limitation when studying susceptibility effects. Other ROIs demonstrate more reasonable agreement with expected values ($$$Y_\text{v}=0.49\dots0.72$$$)^1-4, however more robust fitting procedures and measurement of haematocrit would improve estimation of both $$$\lambda$$$ and $$$Y_\text{v}$$$. Sensitivity to hyperoxia and orientation In the combined data of Figure 4, we observe an increase in $$$Y_\text{v}$$$ during hyperoxia, as expected, demonstrating our method is sensitive to oxygenation changes. This increase translates to a reduction in $$$\langle\Delta\omega\rangle$$$, which is manifested as a reduced frequency difference at longer TE values (Figure 3). Limitations and future work Higher through-plane resolution and greater coverage would improve estimation of vessel geometry, improving the accuracy of $$$Y_\text{v}$$$ quantification. Breath-holding reduced phase artefacts, but also limited the acquisition time and thus resolution/coverage in this study. This new technique must be validated against existing methodologies for single, sub-voxel veins; however, it can also theoretically be expanded to model venous microstructure. Although signal models typically assume small vessels in brain tissue can be described as randomly oriented cylinders⁶, any coherence in the orientation of these cylinders would produce a frequency offset between the intravascular and tissue compartments. We aim to adapt the models presented here to assess whether there is coherent venous orientation in the cortical ribbon of grey matter, and whether useful oxygenation diagnostics can be mapped across the brain using phase data.

Acknowledgements

No acknowledgement found.

References

[1] Lu, H. and Ge, Y. (2008), Quantitative evaluation of oxygenation in venous vessels using T2-Relaxation-Under-Spin-Tagging MRI. Magn. Reson. Med., 60: 357–363. doi:10.1002/mrm.21627

[2] Fan, A. P., Bilgic, B., Gagnon, L., Witzel, T., Bhat, H., Rosen, B. R., & Adalsteinsson, E. (2014). Quantitative Oxygenation Venography from MRI Phase. Magnetic Resonance in Medicine?: Official Journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine, 72(1), 149–159. doi:10.1002/mrm.24918

[3] Sedlacik J, Rauscher A, Reichenbach JR. Quantification of modulated blood oxygenation levels in single cerebral veins by investigating their MR signal decay. Z Med Phys. 2009;19(1) 48-57. doi:10.1016/j.zemedi.2008.07.005. PMID: 19459585.

[4] Driver, I. D., Wharton, S. J., Croal, P. L., Bowtell, R., Francis, S. T., & Gowland, P. A. (2014). Global intravascular and local hyperoxia contrast phase-based blood oxygenation measurements. Neuroimage, 101, 458–465. doi:10.1016/j.neuroimage.2014.07.050

[5] Wharton, S., & Bowtell, R. (2012). Fiber orientation-dependent white matter contrast in gradient echo MRI. Proceedings of the National Academy of Sciences of the United States of America, 109(45), 18559–18564. doi:10.1073/pnas.1211075109

[6] He, X. and Yablonskiy, D. A. (2007), Quantitative BOLD: Mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: Default state. Magn. Reson. Med., 57: 115–126. doi:10.1002/mrm.21108

Figures

Figure 1 An example set of magnitude (a), phase (b) and FDM (c) data from a single volunteer for the echo-time 20 ms. The vessel ROIs are indicated on the magnitude image, the coloured arrows are indicating three vessels selected for the plots in Figure 3. The phase image exhibits severe pertubations from external sources, which are successfully removed by calculating the FDM. FDM retains only the contrast originating from the intravoxel field-variations.

Table 1 Scanning parameters

Figure 2 Boxplot showing fitted values of blood volumes (a) and oxygenation levels (b) for 8 ROIs defined in each scan. In the boxplot (b), reference values for Yv are indicated.

Figure 3 Evolution of the frequency difference of the signal from an ROI containing a single vein, calculated using FDM (a) and the corresponding magnitude decay (b). Three veins were identified with orientations of approximately 0, 30, and 90° (indicated in Figure 1), and data from normoxia (o) and hyperoxia (x) scans are presented with the associated results of the two-compartment model fit. The relatively slower signal decay rate during hyperoxia is consistent with higher venous oxygenation, both in FDM and magnitude plots.

Figure 4 Average frequency offset between the venous and tissue compartments depends on the vessel orientation with respect to the magnetic field $$$\vec{B}_0$$$ represented by angle θ following the relationship $$$f(Y_v)\cdot{}(\cos^2\theta-1/3)$$$. Data from the 8 ROIs identified in the normoxia (blue) and hyperoxia (red) scans are presented, along with best fit curves. The lower amplitude of the fitted curve for the hyperoxia data is consistent with higher Yv. The area around $$$54.7^\circ$$$, the so-called magic angle, is ill-conditioned, since $$$(\cos^2\theta-1/3)\rightarrow0$$$, causing large uncertainy in $$$\langle\Delta\omega\rangle$$$.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3800