Synopsis

The gradient echo and spin echo signal in brain tissue depend both on diffusion and susceptibility effects around and from capillaries, i.e. on structural and functional information that arise from the microvascular networks. In this work, the dependence of the relaxation rates R2 and R2* on capillary radius are considered for a random arrangement of capillaries in the strong collision approximation, and a closed-form solution is derived. Radius maps are then constructed for glioblastoma mice (N=8) to reveal an increased vessel radius in tumorous tissue as compared to non-affected brain tissue.

Target audience

Purpose

Methods

We base our analysis on the well-known model of Yablonskiy and Haacke [1] that describes capillaries as infinitely long, parallel cylinders with a random arrangement and a constant diameter, which is applicable for low capillary volume fractions. Due to the BOLD-effect, each capillary then causes a change of the local Larmor frequency $$$\omega(\mathbf{r})$$$ in form of a dipole field: $$$\omega(\mathbf{r})=\delta\omega R^2\sum_i \frac{\cos(2\phi_i)}{r_i^2}\,,$$$ where $$$\delta\omega=2\pi\gamma B_0\Delta\chi\sin^2(\theta)$$$ is the strength of the dipole field, $$$R$$$ the capillary radius and $$$(r_i,\phi_i)$$$ are the coordinates of the i-th capillary. Diffusion effects can then be included in the weak-field [2] and the strong-collision approximation [3] to obtain closed-form solution of the spin echo and gradient echo signal in dependence on the capillary radius.

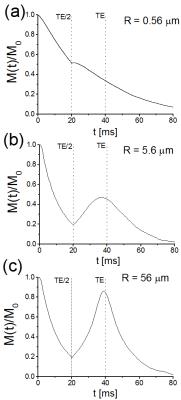
Random walk simulations to obtain gradient echo and spin echo signal were performed with a custom-made C++ code that uses 25000 random walk trajectories for each data point, see Fig. 1.

Animal experiments were performed to obtain capillary radius maps in tumorous and non-tumorous tissue of glioblastoma mice. In total eight 8-10 week old male NMRI nude mice (Charles River Laboratories, Sulzfeld, Germany) were used. A volume of 1 μL (50 000 tumor cells of glioblastoma cell line U87MG ATCC) were stereotactly implanted into the brain cortex in a depth of 500 μm [4]. MR images were obtained on day 28 after tumor implantation at a 9.4 T horizontal bore MR scanner (BioSpec 94/20 USR, Bruker BioSpin GmbH) with a four channel phased array surface coil. 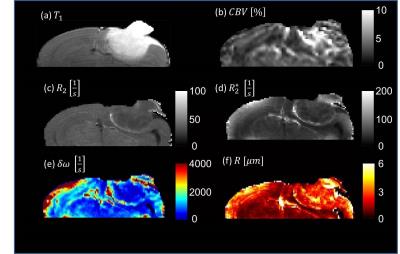Quantitative $$$T_2$$$-maps were measured with a RARE sequence and $$$T_2^*$$$-maps were obtained from a multiecho gradientecho sequence. Dynamic susceptibility contrast (DSC) measurements were performed to acquire cerebral blood volume fractions. Sequence details are provided in Tab.1.

The relaxation rate $$$R_2^*$$$ and cerebral blood volume $$$\eta$$$ were used to calculate the dipole field strength $$$\delta\omega$$$. Spin echo signal, cerebral blood volume and dipole field strength are then used to obtain the capillary radius using the slow-diffusion approximation and assuming a diffusion coefficient of $$$D=1\mu\text{m}^2/ms$$$.

Results

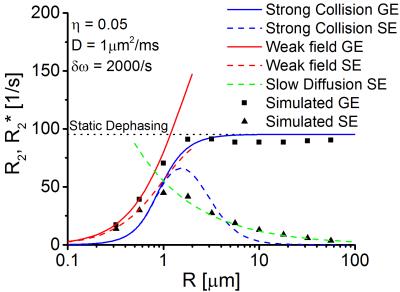
Gradient echo signals are shown in Fig.2: for large capillaries, the relaxation rate $$$R_2^{*}$$$ coincides with the results of Yablonskiy and Haacke. For decreasing radii, diffusion effects lead to an averaging of the experienced magnetic field inhomogeneities and the relaxation rate $$$R_2^{*}$$$ decreases. Random walk simulations agree very well with the weak-field approximation for small capillary radii. However, the strong collision approximation shows a better agreement over the full range of the considered radii.

Since the spin echo signal is inverted at $$$t=TE/2$$$, the spin echo relaxation rate vanishes for large capillary radii (see Fig.2). With decreasing radii, diffusion effects lead to a displacement of spin-bearing particles and the inversion cannot recover the original magnetization (see Fig.1). For very small capillary radii, the spin echo relaxation rate agrees very well with the weak-field model, for large capillary radii, it agrees with the slow diffusion model [6].

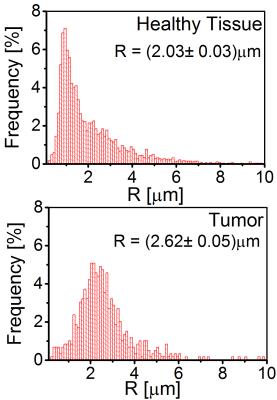
The calculated mean capillary radius in mouse brains shows a significantly increased capillary radius inside the tumor tissue compared to healthy tissue (see Fig. 3 and Fig. 4).

Discussion

Our simulations suggest that, for radii $$$R > 1\mu\text{m}$$$, relaxation rates $$$R_2$$$ and $$$R_2^{*}$$$ are well-described by the slow diffusion approximation and static dephasing limit, respectively. The mean capillary radii in tumor tissue were about 30% larger than in non-affected tissue, in agreement with [7].

It should be noted that we require the dipole field strength to remain constant during measurements which is a reasonable assumption under stable vital conditions. The dipole field strength then provides information on the oxygen extraction fraction, see also [1], however, the weighting between arterial and venous fractions cannot be differentiated. Finally, our method is a promising tool to quantitatively characterize the microvasculator of tumorous tissue that can very easily be embedded into clinical routine.

Acknowledgements

References

[1] D. A. Yablonskiy and E. M. Haacke. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn Reson Med, 32:749–763, 1994.

[2] J. H. Jensen and R. Chandra. NMR relaxation in tissues with weak magnetic inhomogeneities. Magn Reson Med, 44:144–156, 2000.

[3] W. R. Bauer, W. Nadler, M. Bock, L. R. Schad, C. Wacker, A. Hartlep, G. Ertl. Theory of the BOLD effect in the capillary region: an analytical approach for the determination of T2 in the capillary network of myocardium. Magn Reson Med, 41:51–62, 1999.

[4] L. von Baumgarten, D. Brucker, A. Tirniceru, Y. Kienast, S. Grau, S. Burgold, J. Herms, F. Winkler. Bevacizumab has differential and dose-dependent effects on glioma blood vessels and tumor cells. Clin Cancer Res, 17:6192–6205, 2011.

[5] B. P. Chugh, J. P. Lerch, X. Y. Lisa, M. Pienkowski, R. V. Harrison, R. M. Henkelman, J. G.Sled. Measurement of cerebral blood volume in mouse brain regions using micro-computed tomography. Neuroimage, 47:1312–1318, 2009.

[6] V. G. Kiselev, R. Strecker, S. Ziyeh, O. Speck, J. Hennig. Vessel size imaging in humans. Magn Reson Med, 53:553-563, 2005.

[7] M. O. Breckwoldt et al. Correlated magnetic resonance imaging and ultramicroscopy (MR-UM) is a tool kit to assess the dynamics of glioma angiogenesis. eLife, 5:e11712, 2016.