3783

Flip Angle Optimization for Spin-Echo Based Sequences (RARE/TRAPS) for Hyperpolarized Nuclei
Sebastien Bär1, Matthias Weigel2, Dominik von Elverfeldt1, Jürgen Hennig1, and Jochen Leupold1

1Dept. of Radiology, Medical Physics, University Medical Center Freiburg, Freiburg, Germany, 2Radiological Physics, University of Basel Hospital, Basel, Switzerland, Saint Helena

Synopsis

For applications like dynamic imaging, the relatively fast decaying hyperpolarized signal must be acquired over a higher number of sequence cycles and the optimal refocusing flip angle needs to be determined. Optimizing the RARE refocussing flip angles allow to optimize the signal exploitation. Furthermore, optimizing the flip angles of a RARE-based varying flip-angle TRAPS sequence enables an even longer prolongation of the signal lifetime.

Purpose

The RARE sequence is well established in MRI routine and was already successfully used for imaging in hyperpolarization conditions [1]. While the optimal refocusing flip angle is already known (180°) [2,3] for applications like rapid spectroscopic imaging where the signal is acquired over a low number of sequence cycles, for applications like dynamic imaging, the relatively fast decaying hyperpolarized signal must be acquired over a higher number of sequence cycles and the optimal refocusing flip angle needs to be determined. In this study, we show that depending on the echo train length, the optimal RARE refocusing flip angle allowing maximal signal exploitation can be optimized. Even more, we show that a different approach such as the RARE-based varying flip-angle TRAPS sequence (Transitions between pseudo steady states) [4] can help to prolongate the signal lifetime. Subsequent to the optimization of the minimum and maximum flip angles (αMin, αMax) of the sequence, we show that a different acquisition strategy may allow an even longer lasting signal.

Methods

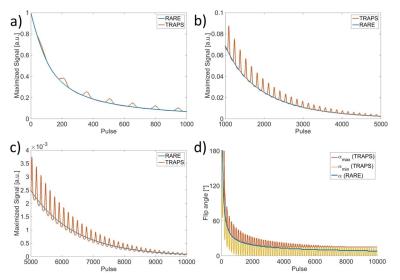
Both the RARE and the TRAPS sequences were simulated in MATLAB based on the extended phase graph (EPG) [5] using the following parameters: 10000 pulses with an echo spacing of 15 ms corresponding to a total measurement time of 150 s. T1 = 25 s and T2 = 2.5 s are typical values for 13C hyperpolarized molecules in solution. For both sequences, the 90° excitation pulse is followed by a first refocusing pulse with flip angle 90°+α/2 that leads to an additional signal gain [6]. Subsequent refocusing pulses were chosen to have either a constant flip angle α (RARE) or the refocusing flip angles were varied (TRAPS) according to the flip angle pattern shown in figure 1. The flip angle ramps from αMin to αMax and the flip angle plateaus (constant αMin or αMax) were chosen to be 128 pulses long. Simulations of the RARE and TRAPS sequences were performed while varying the flip angle α and αMin, αMax with αMin < αMax from 1° to 180° in 1° steps.

Results

The maximal possible signal for each number of pulses from 0 to 10000 pulses was investigated and plotted together with the corresponding optimal flip angles in figure 2. The optimal flip angles maximizing the signal after 150 s (10000 pulses) were found to be α = 9° (RARE) and αMin = 1°, αMax = 15° (TRAPS). The signal evolution over time of both sequences was then investigated while using the optimal flip angles (see figure 3). The TRAPS sequence shows signal plateaus that are higher and lower than the constant decaying RARE-signal.

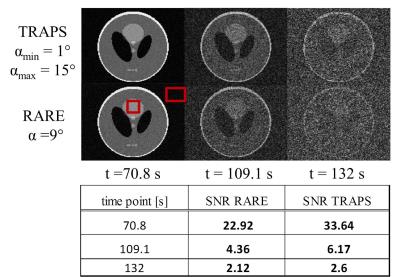
Images (128 x 128 pixels) using a Shepp-Logan phantom were simulated using the RARE and TRAPS signals, while Gaussian noise was added to each of the k-spaces. Three images at later time points (70.8 s, 109.1 s and 132 s) are shown in figure 4. The chosen ROI shows considerably higher SNR in the TRAPS images than in the RARE images with ~47 % and ~23% more signal after 70.8 s and 132 s, respectively.

Discussion/Conclusion

According to our simulations, the RARE sequence is a good candidate when a long-living signal has to be acquired (e.g. in dynamic imaging), provided the 180°-refocusing flip angle is replaced by a lower, optimized flip angle. Besides, we have shown for typical relaxation time values of 13C hyperpolarized molecules in solution (T1 = 25 s and T2 = 2.5 s), that a TRAPS sequence, differing from the RARE sequence only in the flip angle scheme, allows an even longer-lasting signal exploitation. While the here simulated TRAPS images are using only the high signal plateau, optimized acquisition strategies of the k-space may allow increasing the image resolution without losses of SNR. E.g. acquiring the outer and central k-space lines over the low- and high- signal plateaus, respectively, leads to filtering k-space with the TRAPS signal envelope function, with potential impairment on image quality.

Acknowledgements

No acknowledgement found.

References

[1] Golman et al., MRM 46.1: 1-5(2001), [2] Svensson et al., MRM 50:256-262(2003), [3] Leupold et al., Proc. ISMRM 2009, p.2426, [4] Hennig et al., MRM 49.3: 527-535(2003), [5] Weigel et al., JMRI 41.2: 266-295(2015), [6] Hennig et al., MRM 44.6: 983–985 (2000)

Figures

Figure 1: Flip angle scheme of the TRAPS sequence over the pulse numbers. TRAPS ramps the flip angle from αmin to αmax (pulse number n1 to n2) and back to αmin (pulse number n3 to n4), whereat a plateau of constant flip angles with αMin (pulse number n4 to n5) or rather αMax (pulse number n2 to n3) can be introduced.

Figure 2: For each pulse number, the maximal possible flip angle-depending signal was investigated for a RARE and a TRAPS sequence. Simulations are shown for pulse numbers of a) 0 to 1000, b) 1000 to 5000 and c) 5000 to 10000 pulses, corresponding to a measurement time of 0 to 15 s, 15 s to 75 s and 75 s to 150 s respectively. The corresponding optimized flip angles are shown in d). Other simulations parameters: T1 = 25 s and T2 = 2.5 s, ES = 15 ms.

Figure 3: Given that a long-living maximized signal after 150 s is aimed, the signal evolution of a RARE and a TRAPS sequence is shown here using the optimal flip angles (taken from Figure 1) αMin = 1°, αMax = 15° (TRAPS) and α = 9° (RARE).

Figure 4: Simulated images using the TRAPS (αMin = 1°, αMax = 15°) and the RARE (α = 9°) signals. The TRAPS sequence yields higher SNR at later timeframes than the RARE sequence. Here, only the high-signal plateaus of the TRAPS sequence are used. Simulations parameter: image matrix size: 128 pulses, flip angle ramp: 128 pulses, ES = 15 ms, 10000 pulses in total.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3783