3777

Towards Fast Quantitative CEST: A New Model for Quantifying the CEST Effect in the Presence of MT

Alex K Smith^1,2,3, Richard D. Dortch^2,3,4, and Seth A Smith^2,3,4,5

¹FMRIB, University of Oxford, Oxford, United Kingdom, ²Vanderbilt University Institute of Imaging Science, Vanderbilt University, Nashville, TN, United States, ³Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, ⁴Department of Radiology and Radiological Sciences, Vanderbilt University, Nashville, TN, United States, ⁵Department of Ophthalmology, Vanderbilt University, Nashville, TN, United States

Synopsis

Basic models to characterize the CEST effect in vivo suffer from competing magnetization transfer (MT) effects. Here, we use qMT to model the CEST effect and derive CEST indices that are independent of MT. Additionally, simultaneously assessing the MT and CEST effects provides more robust estimates of other elements of the MT effect. Simulations and initial in vivo findings suggest that combining MT and CEST fitting provides a more accurate fit of CEST z-spectra than a traditional single pool Lorentzian fit, and thus provides estimates of the CEST effect that are not dependent on the MT effect.

Purpose

Chemical Exchange Saturation Transfer (CEST) is an MRI technique sensitive to the presence of low concentration mobile protons exchanging with water, such as the backbone amide protons of proteins. While several existing analysis techniques (e.g. Lorentzian difference measurements¹) attempt to quantify these metabolites, they are sensitive to magnetization transfer (MT), caused by large macromolecular molecules, and thus, the accuracy of these CEST analyses are diminished.

Methods to quickly quantify the MT effect in quantitative magnetization transfer (qMT) from a two-pool model of the Bloch-McConnell equations have been developed^2,3, however, several assumptions (no transverse components, saturation pulse approximated as rectangular pulse) are made which prevent this model from being utilized for CEST analyses (offset (Δω)<1kHz)². By removing these assumptions, we have created a two-pool (Water+MT) qMT model that can be solved more rapidly than other quantitative CEST models by generating a fit to a CEST+qMT z-spectra, simultaneously estimating the CEST effect free of MT interference, and the macromolecular composition in tissue.

Methods

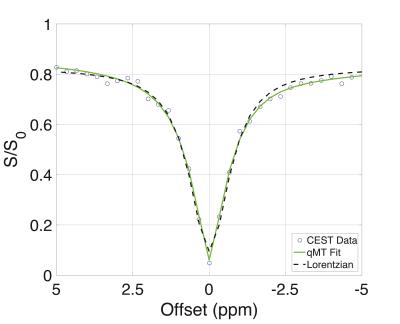
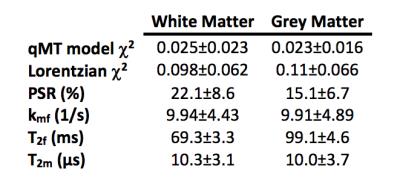
All analyses were performed in MATLAB (Mathworks, Natick, MA). Monte Carlo simulations were performed by numerically simulating a two-pool model (Water+MT) of the Bloch-McConnell equations for typical values for white matter (WM) and grey matter (GM) (Table 1). Simulated CEST data was generated using a 2µT, 75-ms sinc-Gauss pulse over 31 offsets evenly spaced between ±5ppm; qMT data was generated using a 20-ms sinc-Gauss pulse with saturation flip angle $$$\alpha_{MT}$$$= [360°,820°], and Δω=1, 1.5, 2, 2.5, 8, 16, 32, 100kHz. Gaussian noise was added (SNR=60), and the qMT model fit was performed over 1,000 noise realizations. $$$\chi^2$$$-values were calculated over each noise realization to evaluate the goodness-of-fit. A Lorentzian fit¹ was also performed to compare the qMT model against an established CEST analysis technique.

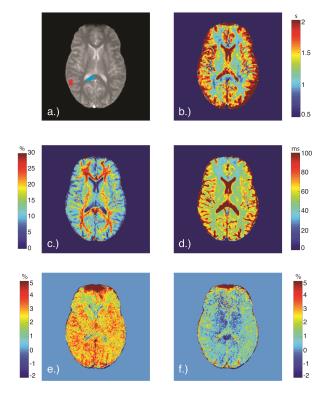
A single volunteer (female, 22 years old) was imaged in a 3T Achieva scanner (Philips, the Netherlands). A two-channel body coil was used for excitation, and a 32-channel head coil was used for signal reception. Two SPGR experiments were performed: a qMT acquisition and a CEST acquisition sensitized to amides (APT). The CEST protocol was acquired using a 2μT, 150-ms sinc-Gauss pulse over 36 offsets, applied asymmetrically between ±5ppm with a TR/TE/$$$\alpha_{EX}$$$/EPI-Factor=302-ms/8.6-ms/15°/7. The MT protocol was performed using a 20-ms, sinc-Gauss pulse with a TR/TE/$$$\alpha_{EX}$$$/EPI-Factor=50-ms/7.4-ms/10°/5, $$$\alpha_{MT}$$$= [360°,900°], and Δω=1, 1.5, 2, 2.5, 8, 16, 32, 100kHz. B1, B0, and T₁ acquisitions were also acquired to correct for field inhomogeneities and to independently calculate T₁ maps⁴. All acquisitions used a FOV of 220x220x20-mm³ over four slices, SENSE=2, at a resolution of 1x1x5-mm³.

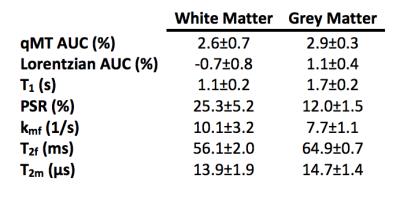
Normalized (to S0) MT and CEST data were used to generate qMT parameter maps for each voxel using the qMT model to estimate the macromolecular (m) to free (f) pool size ratio (PSR), exchange rate (k_mf), and relaxation times $$$(T_2^{f,m})$$$. The qMT parameter maps were then used to generate signal data from 3-4ppm, and the APT-CEST effect was calculated by finding the integral of the residuals (difference between CEST data and generated fits), a so-called area under the curve (AUC) analysis, from 3-4ppm. The data was also fit to a Lorentzian function¹ to compare with established techniques.

Mean AUC values for the qMT and Lorentzian models, and for all qMT parameters, were calculated from manually-defined regions of interest (ROI) in the GM and WM (Figure 2). The mean values for each tissue type and fitting methodology were then compared.

Results

Figure 1 and Table 2 demonstrate fitting results using the Lorentzian and qMT models. Incorporating the MT pool into the CEST data significantly improves the fit (Wilcoxon rank-sum test between qMT and Lorentzian model $$$\chi^2$$$-values=p<0.001 for WM and GM), while still estimating qMT values close to what was prescribed (Table 2). Figure 2 and Table 3 display the in vivo results. The qMT model provides higher AUC than the Lorentzian model: importantly, the qMT model shows no WM/GM differences, consistent with recent reports of APT-CEST in healthy volunteers⁵. Furthermore, the estimated mean qMT parameters are consistent with established qMT parameter estimates² (Table 3), with the exception of $$$T_2^f$$$, which shows elevated values more closely matched with T₂ values from the literature⁶, indicating points close to 0ppm may provide a more accurate representation of the free pool than other qMT models.

Discussion

We demonstrate a more quantitative characterization of the APT-CEST effect than has been previously described using MT to inform the fitting method. These findings provide insight into providing quantitative CEST metrics free from the influence of MT effects, and thus, are a more unbiased measure of the CEST effect than is currently available.

Acknowledgements

Funding provided by: Whitaker International Program Fellowship, NIH/NCI R25 CA136440, DOD W81XWH-13-0073, NIH/NIBIB R21 NS087465-01, NIH/NIBIB R01 EY023240 01A1 and The National MS Society.

References

1. Jones, CK, et al. MRM, 2012. 67(6): p. 1579-1589.

2. Yarnykh, VL. MRM, 2002. 47(5): p. 929-939.

3. Listerud, J. MRM, 1997. 37(5): p. 693-705.

4. Smith, SA, et al. MRM, 2008. 60(1): p. 213-219.

5. Khlebnikov, V, et al. JMR, 2016. 272: p. 82-86.

6. Lu, H, et al. JMRI, 2005. 22(1): p. 13-22.

Figures

Table 1: White matter and grey matter values used for the simulations. Values were chosen from typical values in each respective tissue.

Figure 1: Example simulated white matter data from data generated from the two-pool Bloch-McConnell equations with an SNR of 60 (blue circles), as well as the resulting curves from the fits for the qMT model (green lines) and Lorentzian fit from Jones et al¹ (black dashes). The qMT model much more closely aligns with the simulated data than the Lorentzian fit, and, importantly, fits the asymmetry present from the macromolecular pool.

Table 2: Mean±SD values estimated from the simulations of the qMT model and Lorentzian fits. The qMT model displays significantly better fits compared to the Lorentzian model (p < 0.001 in all cases). Furthermore, the estimated mean qMT parameter values are approximately equal to the starting parameter values.

Table 3: Mean±SD values for ROIs drawn in the WM and GM of the brain. The qMT AUC(3-4ppm) displays similar values between GM and WM, consistent with recent literature, while the Lorentzian AUC(3-4ppm) displays large WM/GM differences. Strikingly, the WM AUC is negative, indicating the Lorentzian model passes below the data. The qMT parameters also display values reflective of established values, with the exception of the $$$T_2^f$$$, which displays values much higher than previous estimates.

Figure 2: a.) Anatomical image of a single slice of the imaging volume with ROIs in the WM (blue) and GM (red), b.) T₁ map calculated from an independent measurement of T₁⁴, estimates of the c.) PSR and d.) $$$T_2^f$$$. Estimates of the AUC from the qMT model (e.) and Lorentzian model (f.). No WM/GM contrast is seen in the qMT model, which is consistent with recent literature, as opposed to the AUC from the Lorentzian model, which displays under-fitting of the CEST spectrum in WM areas.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3777