Purpose

Chemical exchange saturation transfer (CEST) imaging is a new MRI contrast approach and many promising applications have been proposed, such as cancer and stroke [1]. CEST imaging is time-consuming and fast acquisition is highly desired. As the new emergency of compressed sensing (CS) theory [2-4], several works have been developed to accelerate CEST with CS [5-8]. However, to the best of our knowledge, no experimental implementation of a Cartesian undersampled CS scheme with CEST had been reported. In this study, we design random Cartesian sampling [4] sequence and golden angle radial (GAR) [9] sampling sequence and use the low rank plus sparse matrix decomposition (L+S) method [10] to reconstruct the truly undersampled phantom and in vivo human brain data.

Acquisition Method

Experiments were performed on a Philips 3T Ingenia system using a 32-channel head coil. Cartesian random sampling scheme uses the variable density undersampling pattern [4]. After the saturation pulses, the k-space lines are acquired with a low-high order as shown in Fig. 1. The low frequency k-space is fully sampled first and then high frequency k-space is randomly sampled. Compared to the linear order, which samples from the bottom of k-space to the top, low-high order acquires the most important low frequency information before T₁ recovery diminishes the CEST effects. Radial sampling follows an angular increment of 111.25°, which is designed to make the x and y gradients performs as: $$$Gy/Gx=tan^{-1}(n*111.25)$$$, where n is the number of spokes. The CEST images for human brain were acquired with a TSE sequence, TR/TE=4200/6.4ms, slice thickness=4.4mm, FOV=240x240mm, 21 points swept between ±1000Hz in steps of 100Hz with one additional image without saturation for normalization. Phantom consists of iopamidol solution with pH values of 6.0 and 7.5. The CEST for phantom used similar parameters for brain, only FOV=224x224mm. In all experiments, saturation RF consisted 10 hyper-secant pulses, each of 49.5ms duration with 0.5ms intervals, and saturation power is 1.6μT for human brain and 1.2μT for phantom. CEST processing used WASSR [11] for B₀ inhomogeneity correction. For fully sampled acquisitions, Cartesian and GAR samplings were used in phantom and Cartesian sampling in human. In the CS acquisitions, the Cartesian undersampling pattern was used with the reduction factor R=5 for phantom and R=4 for brain. The GAR spokes were 224 and 56.

Reconstruction Method

In CEST imaging, voxels in the same compartment have similar z-spectra [6]. The high spatiotemporal correlation is suitable for the low rank matrix model. L+S decompose the CEST images matrix as a summation of a low-rank matrix (few non-zero singular values) and a sparse matrix (few non-zero elements). Specifically, the reconstruction algorithm tries to solve this problem: $$$\min_{L,S}\parallel F(L+S)-d\parallel_2^2+\alpha\parallel L\parallel_*+\beta\parallel S\parallel_1$$$, where $$$F$$$ is the undersampling Fourier operator, $$$d$$$ is the undersampled k-space data, $$$\parallel \cdot\parallel_*$$$ is the nuclear norm to regularize the sparsity of the low-rank matrix $$$L$$$, $$$\parallel \cdot \parallel_1$$$ is the l₁-norm to regularize the sparsity of the sparse matrix $$$S$$$, $$$\alpha$$$ and $$$\beta$$$ are regularization parameters.

Results and Discussion

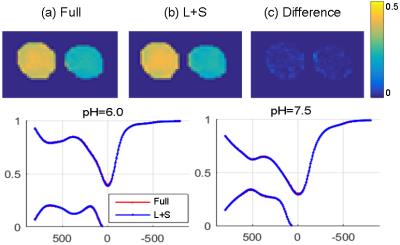
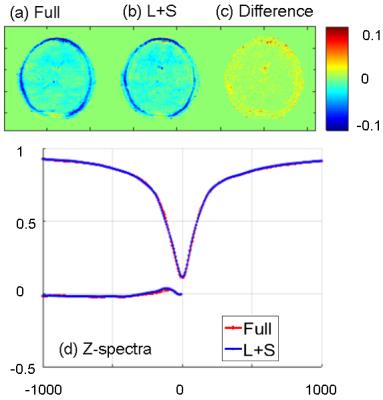
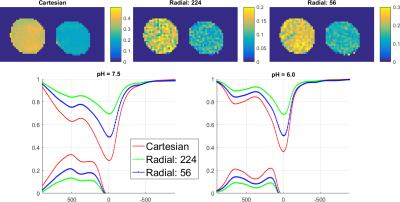
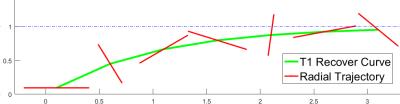
Fig. 2 compares MTR_asym map and z-spectra between the reconstruction of Cartesian fully sampled and undersampled phantom for different pHs. The CEST effects are measured at 4.2ppm. The reconstruction is very close to the fully sampled case. Fig. 3 demonstrates the APT maps for brain data, and the undersampled result is similar to the fully sampled one but there is some difference at the center part, which might be due to the volunteer’s motion between the acquisitions or the B₀ inhomogeneity. Fig. 4 compares the reconstruction of fully sampled Cartesian and GAR of phantom. The reconstruction of 224 spokes has a smaller CEST effects than 56 spokes, and both of them are smaller and more inhomogeneous than Cartesian one. The possible explanation is presented in Fig. 5: the linear radial sampling is implemented, which means every radial k-space line goes through the k-space center. Thus, the total CEST effect in the image is an average along the T₁ recovery curve, and the CEST effect should be smaller than the low-high order Cartesian acquisition. Less spokes acquires data only at the beginning of T₁ recovery, so the CEST effect is larger in the heavier undersampled radial scheme.

Conclusion

We experimentally designed the undersampled Cartesian and GAR CEST sequence, and tested in the phantom and in vivo data. Phantom results demonstrate the undersampled Cartesian scheme performs similar to the fully sampled case. The radial sampling leads to decreased CEST effects compared to the Cartesian one. Work is underway to conduct additional in vivo experimental tests and to analyze different undersampling schemes.

Acknowledgements

The authors thank Dr. Ricardo Otazo (New York University) for making the low rank plus sparse matrix decomposition (L+S) code available online. The authors thank Dr. Asghar Hajibeigi (University of Texas Southwestern Medical Center) for phantom preparation. This work is supported in part by the NIH grant R21.