3715
Correction of off-resonance for T1 and T2 mapping using phase-cycled inversion-recovery balanced steady state free precession1Research Imaging Institute and Ophthalmology, University of Texas Health Science Center, San Antonio, TX, United States, 2Research Imaging Institute, University of Texas Health Science Center, San Antonio, TX, United States, 3Biomedical Engineering, University of Texas at San Antonio, San Antonio, United States
Synopsis
Fast measurement of T1 and T2 can be made using inversion-recovery Look-Locker (LL) bSSFP methods. However, the LL-bSSFP signal is dependent on the off-resonance frequency which can affect calculated T1 and T2. In this study we develop and test methods to correct for effects of off-resonance on T1 and T2 calculation using multiple phase-cycled LL-bSSFP. The phase-cycled LL-bSSFP data could be combined with a maximum-T1* projection method to improve T1 and T2 accuracy in the case of off-resonance.
Purpose
Fast measurement of T1 can be made using inversion-recovery Look-Locker (LL) methods in which multiple measurements at different inversion times are made after a single inversion pulse.1 Balanced steady state free precession (bSSFP) readouts provide high SNR compared to spoiled gradient echo sequences and additionally allow for T2 measurement.2 However, the LL-bSSFP signal is dependent on the off-resonance frequency which can affect calculated T1 and T2. In this study we develop and test methods to correct for effects of off-resonance on T1 and T2 calculation using multiple phase-cycled LL-bSSFP.Methods
The
transient bSSFP signal evolves with effective relaxation rates, which when
properly prepared and for a wide range of off-resonance frequencies is
approximately monoexponential with only small oscillations.3 Even if
image artifacts from oscillations are avoided, the values of T1 and T2 calculated
from LL-bSSFP as in2 will still have inaccuracies at off resonance.4
Two approaches to combine phase-cycled LL-bSSFP were investigated. For both
approached, three parameter fits for the apparent relaxation time T1*
were performed as in2 for data with 4 different RF phase increments.
The phase-cycle dataset with largest residuals from the fit was discarded
pixel-by-pixel. 1) Maximum T1* projection (MTP): T1* as a function of
off-resonance frequency has a maximum on-resonance and minimum at 180o
off-resonance, so the single phase-cycle data with maximum T1* was
assumed to be nearly on-resonance and used for calculating T1 and T2
as in.2 2) Non-linear averaging (NLA): the remaining three phase-cycled
data were averaged then refit for T1* from the NLA data and calculating T1 and
T2 as in.2
LL-bSSFP Bloch simulations were run over a range of off-resonance frequencies with multiple T1/T2 and flip angles, phase-cycling of 0, 90, 180, and 270o, TR/TE=5/2.5ms, instantaneous RF pulses, 180o inversion, and linear ramp of 7 preparation pulses. The number of excitations was varied (from 640-2740) to allow substantial recovery steady state for each T1/T2/flip angle. T1 and T2 were calculated as given above.
Results
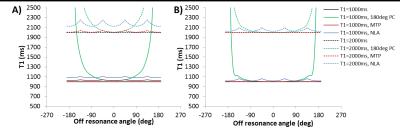
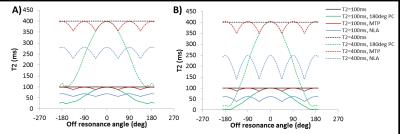
From simulated data, the calculated T1 (Fig 1) and T2 (Fig 2) are shown from different methods. The MTP method was the only one to give reasonably consistent values for off-resonant data, although there were some periodic deviations from the correct values. Lower flip angle reduced the off-resonant error for T1, but had little effect on T2.Discussion
The MTP method could reduce off-resonance artifacts for T1 and T2 mapping using LL-bSSFP, while the NLA method does not provide accurate values. This demonstrates that simple methods used to correct banding in steady state bSSFP images, such as NLA, cannot simply be applied for quantitative relaxometry. A previous study used a similar method to the maximum-T1* projection for T2 mapping using LL-bSSFP, but selecting the phase-cycle set to use based on T2 minima and maxima rather than T1*.4 Acquisition of 4 phase-cycles increases scan time and the use of only 1 of 4 datasets to calculate T1 and T2 reduces SNR, so further methods that require fewer phase-cycle datasets or uses more of the data would be of interest. In conclusion, the phase-cycled LL-bSSFP data can be combined with the maximum-T1* projection to improve T1 and T2 accuracy in the case of off-resonance.Acknowledgements
Eric Muir, PhD holds a Voelcker Fund Young Investigator Award from the Max and Minnie Tomerlin Voelcker Fund.References
1) Brix G, Schad LR, Deimling M, et al. Fast and precise T1 imaging using a TOMROP sequence. Magn Reson Imaging 1990;8:351–356. 2) Gulani V, Schmitt P, Griswold MA, et al. Towards a Single-Sequence Neurologic Magnetic Resonance Imaging Examination: Multiple-Contrast Images From an IR TrueFISP Experiment. Invest Radiol 2004;39:767-774. 3) Schmitt P, Griswold MA, Gulani V, et al. A simple geometrical description of the TrueFISP ideal transient and steady-state signal. Magn Reson Med 2006;55:177-186. 4) Pelot NA and Bowen CV. Quantification of superparamagnetic iron oxide using inversion recovery balanced steady-state free precession. Magn Reson Imaging 2013:31:953-960.Figures