3675

Improved Morphology Enabled Dipole Inversion for Quantitative Susceptibility Mapping by Using Prior Information
Yihao Guo1, Li Guo1, Yingjie Mei1,2, Jijing Guan1, and Yanqiu Feng1

1Guangdong Provincial Key Laboratory of Medical Image Processing,School of Biomedical Engineering, Southern Medical University, Guangzhou, People's Republic of China, 2Philips Healthcare, Guangzhou, China.

Synopsis

Morphology enabled dipole inversion (MEDI) has been proposed to reconstruct QSM without obvious streaking artifacts at the smooth regions of susceptibility map. However, reconstruction errors or streaking artifacts near edges are not addressed by MEDI. In this work, we aim to improve MEDI by constraining the edges of susceptibility map with prior information.

Purpose

Morphology enabled dipole inversion (MEDI) [1, 2] can successfully reconstruct susceptibility map from a single-orientation field map without obvious streaking artifacts. However, MEDI enforces only the total variation constraint in smooth regions with negligible gradients in magnitude images, and imposes no constraints in the regions near edges. Thus, reconstruction errors or streaking artifacts near edges are not addressed by MEDI. In this work, we aim to improve MEDI by further introducing edges constraints based on prior information to the susceptibility reconstruction.

Methods

The proposed method can be formulated as:

$$$\chi=argmin\parallel F^{-1}DF\chi-\psi\parallel_2^2+\lambda_{1}\parallel MG\chi\parallel_{1}+\lambda_{2}\parallel (1-M)(G\chi-G\chi_{p})\parallel_{1}$$$ (1)

where $$$ \chi$$$ is the underlying susceptibility map, $$$\psi$$$the tissue field, F the discrete Fourier transform, D the dipole kernel in the k-space,$$$\parallel\parallel_2^2$$$the L2 norm, M a binary mask of smooth regions in magnitude image, G the gradient operator in three spatial dimensions,$$$\parallel\parallel_1$$$ the L1 norm, $$$\chi_{p}$$$the prior information and $$$\lambda_{1} $$$and $$$\lambda_{2}$$$ the regularization parameters.The second term enforces the smooth regions of susceptibility map matching those of magnitude image. The third term requires the gradient of susceptibility map close to that prior gradient information to insure clear structure and reduce reconstruction errors at the edge voxels.

The prior information$$$ \chi_{p}$$$ in Eq. (1) is obtained by combining the L2 norm constrained QSM $$$\chi_{0}$$$ with traditional TKD QSM $$$\chi_{TKD}$$$ [3] in the k-space [4]:

$$$\chi_{p}=F^{-1}[\frac{1}{\alpha+D^{2}}(\alpha F\chi_{0}+D^{2}F\chi_{TKD})]$$$ (2)

where $$$ \alpha$$$is a parameter controlling the weight and set to 0.1 in all experiments. The in Eq. (2) is the result of L2 norm constrained QSM $$$ \chi_{0}$$$ and expressed as:

$$$\chi_{0}=argmin\parallel F^{-1}DF\chi-\psi\parallel_2^2+\beta_{1}{\parallel MG\chi\parallel_{2}^2}+\beta_{2}\parallel (1-M)(G\chi-G\chi_{TKD})\parallel_2^2$$$ (3)

where $$$\beta_{1} $$$and $$$\beta_{2} $$$are regularization parameters. The second term minimizes the gradient of susceptibility map in regions with negligible gradient in magnitude image and thus suppresses streaking artifacts in these regions. The third term aims to preserve the TKD gradient information in the susceptibility map.

To evaluate the performance of the proposed method, the numerical simulation, gadolinium phantom and in vivo human brain sets from the online QSM repository [5] were reconstructed by MEDI and the proposed methods.

Results

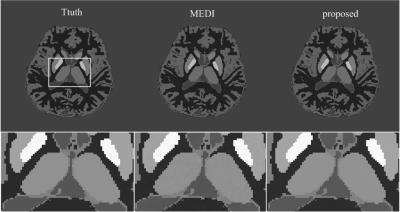
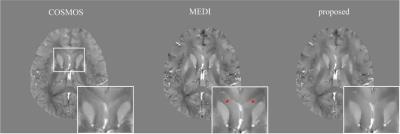
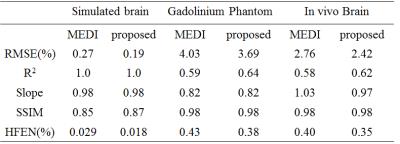
In the numerical simulation results (Fig.1), the MEDI method generated uneven effects in the flat regions, e.g. in thalamus, while the proposed method generated homogeneous result similar to the truth. In the gadolinium phantom results (Fig.2), the proposed method suppressed the streaking artifacts which were observed in the result of MEDI (red arrows). In vivo human brain results (Fig.3), artifacts can be seen at the boundary of caudate nucleus in the result of MEDI (red arrows), while these artifacts were alleviated in the result of the proposed method, which was close to the COSMOS result. In Table 1, the proposed method reduced root mean square errors (RMSE) and high frequency error norm (HFEN) and improved determination coefficient (R2) compared to MEDI method in numerical simulation, gadolinium phantom and in vivo data.

Discussion

A novel framework based on the prior information was proposed for obtaining QSM form single-orientation field map. In the proposed method, the prior information can effectively constrain the edges of susceptibility map and thus suppress the streaking artifacts.

Conclusion

The numerical simulation, gadolinium phantom and in vivo human brain results demonstrate that the prior information can be effectively employed to achieve accurate reconstruction of susceptibility mapping. This framework can be further explored with other prior information for improving QSM.

Acknowledgements

No acknowledgement found.

References

[1] T. Liu MRM 2011;66:777-83

[2] J. Liu MRM 2012;59:2560-8

[3] K. Shmueli MRM 2009;62:1510-22

[4] Y. Wen MRM 2016;75:823-830

[5] Online QSM repository. http://weill.cornell.edu/mri/QSM/Online.zip.

Figures

Figure 1. The QSM reconstructed by MEDI and the proposed method in a numerical simulation.

Figure 2. The QSM reconstructed by MEDI and the proposed method in a gadolinium phantom.

Figure 3. The QSM reconstructed by MEDI and the proposed method in vivo human brain.

Table 1 Accuracy of the results with MEDI and the proposed method

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3675