3647
Volumetric Reconstruction of Tissue Electrical Properties from B1+ and MR Signals Using Global Maxwell Tomography: Theory and Simulation Results.1Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Center for Computational and Data-Intensive Science and Engineering, Skolkovo Institute of Science and Technology, Moscow, Russian Federation, 3The Sackler Institute of Graduate Biomedical Science, New York University School of Medicine, New York, NY, United States, 4Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States
Synopsis
Magnetic resonance-based inverse scattering has been proposed to extract tissue electrical properties (EP). We present an improved implementation of the Global Maxwell Tomography (GMT) EP mapping technique, with two new cost functions and an extension that uses piecewise linear basis functions to represent fields for higher accuracy. GMT does not make symmetry assumptions, is fully 3D, and is robust to noise. We validated the new GMT version with various numerical experiments, using a heterogeneous head model with realistic EP and a phantom with tissue-mimicking EP. We showed, for the first time, that artifact-free accurate reconstruction of EP is possible.
Purpose
Magnetic resonance (MR)-based inverse scattering has been proposed to extract tissue electrical properties (EP), namely electric permittivity and conductivity, noninvasively. The majority of the existing approaches rely on direct inversion of the differential form of Maxwell’s equations1-4, which result in noise amplifications and boundary artifacts, due to numerical derivatives. Using the integral form of Maxwell’s equations avoids the need to take derivatives of noisy data completely. Two techniques based on integral equations have been proposed: CSI-EPT5, which relies on symmetry assumptions in order to improve conditioning, and Global Maxwell Tomography (GMT)6-7, which makes no assumptions and solves for all EP in a volume of interest with a single optimization. The aim of this work is to present an improved version of GMT, based on new computational tools.Theory
GMT starts by simulating the transmit $$$B_1^+$$$ field and MR signal ($$$S$$$) in the sample, given the incident field from radiofrequency (RF) sources and an initial guess for the EP. Then it updates the EP based on the minimization of the error between measured and simulated data. Our proposed implementation of GMT includes two cost functions that can be minimized independently or simultaneously as a weighted sum. Compared to the original implementation of GMT6-7, this version also incorporates relative phase information between transmit and receive coils in both $$$B_1^+$$$ and $$$S$$$.
The first cost function operates on $$$B_1^+$$$ maps:
$$f(\epsilon)=\frac{\sqrt{\sum_k\sum_n\| |\hat{b}_k|\odot |\hat{b}_n|\odot e^{j(\hat{\phi}_k-\hat{\phi}_n)}-b_k(\epsilon)\odot\overline{b_n(\epsilon)}\|_2^2}}{\sqrt{\sum_k\sum_n\| |\hat{b}_k|\odot |\hat{b}_n|\|_2^2}}\text{,}$$
where $$$|\hat{b}_k|$$$ denotes reference map $$$k$$$, and $$$e^{j(\hat{\phi}_k-\hat{\phi}_n)}$$$ denotes the relative phase factor.
The second cost function operates on signal measurements directly:
$$f(\epsilon)=\frac{\sqrt{\sum_k\sum_l\|\hat{s}_{kl}-m\odot b^+_k\odot b^-_l\odot\text{sinc}\!(\alpha|b_k^+|)\|_2^2}}{\sqrt{\sum_k\sum_l\|\hat{s}_{kl}\|_2^2}}\text{,}$$
where $$$b^+_k$$$ indicates $$$B_1^+$$$ map $$$k$$$, $$$b_l^-$$$ indicates $$$B_1^-$$$ map $$$l$$$. In the current implementation we assumed that the complex-valued spin magnetization ($$$m$$$) is roughly constant, which is valid for simulations. A future GMT extension will infer $$$m$$$.
Methods
We employed MARIE8-9, which computes the electromagnetic (EM) fields by approximating them with piecewise constant basis functions. We also tested a new extension of MARIE that uses discontinuous piecewise linear basis functions, which increases simulation time, but also improves accuracy and accelerates convergence. Numerical gradients of the cost functions were calculated analytically via adjoint formulations. The quasi-Newton L-BFGS-B10-11 was used to accelerate convergence, while maintaining physical values for the EP.
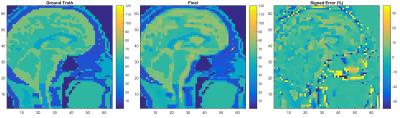
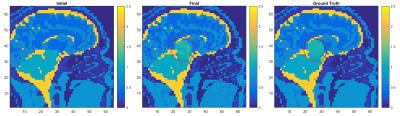
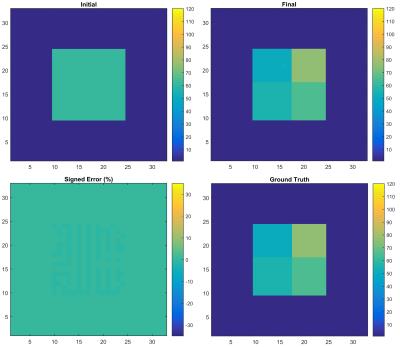
To evaluate our new GMT implementation, we performed three numerical experiments at 7T. In our first experiment, we used GMT based on piecewise constant basis functions to infer the electrical properties of the Duke head model12, starting from a homogeneous initial guess and employing sixty-four signal maps (SNR=120 and 3mm3 resolution) simulated for a 8-element Tx-Rx array13. In addition, an L0-based total variation regularizer was used in a second stage of the optimization. In the second experiment, we aimed at detecting tumors ($$$\sigma\approx 1.2\text{S/m}$$$) artificially inserted into the Duke head model12 using the tumor-free model as the initial guess. For this case, we used the same coil model and EM solver, but only the $$$B_1^+$$$-based cost function, with SNR=100 for the eight $$$B_1^+$$$ maps. In the third experiments, we constructed a cylindrical SVD basis with ideal piecewise linear current sources. We then used the first eight principal components as RF sources in GMT to reconstruct EP for a tissue mimicking 4-compartment phantom (6mm3 isotropic resolution). For this case, the $$$B_1^+$$$-based cost function was employed and, as proof of principle, we did not add noise to the $$$B_1^+$$$ maps.
Results and Discussion
The first experiment ran for 500 iterations, followed by 300 iterations with the regularizer. The average relative error was 10% in relative permittivity (Fig.1) and 20% for conductivity (not shown). However, note that error is almost zero within the brain region. The second experiment ran for 500 iterations, and the locations and EP of the tumors were correctly inferred (Fig.2), although the maps were blurred. We expect results will further improve when minimizing both cost functions simultaneously. The third experiment lasted 384 iterations (Fig.3) and EP reconstruction was nearly perfect (max error <1.4%). Note that this is the first time that artifact-free accurate EP maps are shown, even for a noise-free case.Conclusion
We presented and assessed a new implementation of GMT. We proved that GMT can reconstruct electrical properties perfectly in the absence of noise using only 8 $$$B_1^+$$$ maps as input. We also showed that GMT is robust in the presence of noise. Future work will include demonstration of GMT in actual experiments, using piecewise linear basis functions and a cost function combining both signal and $$$B_1^+$$$. Parallelization over multiple GPUs will be explored to reduce simulation time.Acknowledgements
This work was supported in part by the research grant NSF CAREER 1453675 and the Center for Advanced Imaging Innovation and Research (www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).References
1. U. Katscher, T. Voigt, C. Findeklee, P. Vernickel, K. Nehrke, and O. Dossel, “Determination of Electric Conductivity and Local SAR Via B1 Mapping,” IEEE Trans. Med. Imaging, vol. 28, no. 9, pp. 1365–1374, Aug. 2009.
2. Sodickson DK, Alon L, Deniz CM, Brown R, Zhang B, Wiggins GC, Cho GY, Eliezer, NB, Novikov DS, Lattanzi R, Duan Q, Sodickson L and Zhu Y, Local Maxwell tomography using transmit-receive coil arrays for contact-free mapping of tissue electrical properties and determination of absolute RF phase; 20th Scientific Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM). Melbourne (Australia), 5-11 May 2012, p. 387.
3. J. P. Marques, D. K. Sodickson, O. Ipek, C. M. Collins, and R. Gruetter, “Single acquisition electrical property mapping based on relative coil sensitivities: A proof-of-concept demonstration,” Magn. Reson. Med., vol. 74, no. 1, pp. 185–195, Aug. 2014.
4. J. Liu, X. Zhang, S. Schmitter, P.-F. Van de Moortele, and B. He, “Gradient-based electrical properties tomography (gEPT): A robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging,” Magn. Reson. Med., vol. 74, no. 3, pp. 634–646, Sep. 2014.
5. E. Balidemaj, C. A. T. van den Berg, J. Trinks, A. L. van Lier, A. J. Nederveen, L. J. Stalpers, H. Crezee, and R. F. Remis, “CSI-EPT: A Contrast Source Inversion Approach for Improved MRI-Based Electric Properties Tomography,” IEEE Trans. Med. Imaging, vol. 34, no. 9, pp. 1788–1796, Aug. 2015.
6. J. E. C. Serralles, A. G. Polymeridis, M. Vaidya, G. Haemer, J.K. White, D. K. Sodickson, L. Daniel and R. Lattanzi, “Global Maxwell Tomography: a novel technique for electrical properties mapping without symmetry assumptions or edge artifacts,” 24th Scientific Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM). Singapore, 7-13 May 2016, p. 2993.
7. J.E.C. Serrallés, L. Daniel, J.K. White, D.K. Sodickson, R. Lattanzi, & A.G. Polimeridis (2016, October). Global Maxwell Tomography: A novel technique for electrical properties mapping based on MR measurements and volume integral equation formulations. In Antennas and Propagation (APS-URSI), 2016 IEEE International Symposium on (pp. 1395-1396).
8. J. F. Villena, A. G. Polimeridis, Y. Eryaman, E. Adalsteinsson, L. L. Wald, J. K. White, and L. Daniel. “Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods.” IEEE Transactions on Biomedical Engineering, 63 (11): 2250-2261, 2016.
9. A.G. Polimeridis, J.F. Villena, L. Daniel, J.K. White. “Stable FFT-JVIE solvers for fast analysis of highly inhomogeneous dielectric objects,” Journal of Computational Physics, Volume 269, 15 July 2014, Pages 280-296, ISSN 0021-9991, http://dx.doi.org/10.1016/j.jcp.2014.03.026.
10. R. H. Byrd, P. Lu and J. Nocedal. “A Limited Memory Algorithm for Bound Constrained Optimization," (1995), SIAM Journal on Scientific and Statistical Computing, 16, 5, pp. 1190-1208.
11. S. Becker, "L-BFGS-B-C," GitHub, 2015. [Online]. Available: https://github.com/stephenbeckr/L-BFGS-B-C. Accessed: Nov. 9, 2016.
12. M. C. Gosselin, E. Neufeld, H. Moser, E. Huber, S. Farcito, L. Gerber, M. Jedensjö, I. Hilber, F. Di Gennaro, B. Lloyd, E. Cherubini, D. Szczerba, W. Kainz, N. Kuster, “Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0”, Physics in Medicine and Biology, 59(18):5287-5303, 2014.
13. G.C. Wiggins, B. Zhang, G. Chen and D.K. Sodickson. “A Highly Decoupled 8 Channel Transmit-Receive Loop Array for 7T with Diverse B1 Profiles”, 20th Scientific Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM). Melbourne (Australia), 5-11 May 2012, p.309.
Figures