3646
Data-Driven Background Phase Correction and Combination to Improve the Accuracy of MR-EPT with Multi-Channel Receivers1Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States
Synopsis
We propose a method for combining phase data from multiple receiver channels for phase-based conductivity mapping that does not require a reference scan or reference coil. The proposed method combines a background phase removal step, to reduce bias from individual coil phases, and local coil compression, which maximizes SNR in the combined phase data.
Purpose
To develop a method for combining phase data from multiple receiver channels for phase-based conductivity mapping that does not require a reference scan or reference coil.Methods
Multi-coil receiver arrays can improve image SNR, which is advantageous for MR electrical properties tomography (MR-EPT) because the Laplacian operator used in the calculations amplifies noise. Optimal Combine1 (OC) is considered the gold standard for combining multi-channel data because coil sensitivities are calculated from multi-channel and body coil images. However, the body coil acquisition is time consuming and has low SNR. Adaptive Combine2 (AC) calculates global coil combination weights using the eigendecomposition of the acquired data, eliminating the need for an extra scan. We have previously proposed the use of Local Coil Compression3 (LCC) for MR-EPT, which also calculates coil weights using the eigendecomposition, but over small neighborhoods to account for spatially varying coil sensitivities. However, when an object is too close to an individual coil, the combined phase is biased by that coil’s rapidly varying phase due to the high coil sensitivity. Therefore, we propose a data-driven relative phase removal prior to coil compression to reduce bias due to relative coil phase.
One can express the phase in an individual coil as
$$\phi_j=\phi_{j,rel}+\phi_{common}$$
where $$$\phi_{j,rel}$$$ is the relative spatial phase profile for coil j and $$$\phi_{common}$$$ is the common phase among all coils, including the object phase and object independent phase, such as phase due to off-resonance. For MR-EPT, we are interested in the object phase. Common object independent phase can be minimized with an appropriate acquisition, but we must eliminate the relative spatial phase.
First we calculate the product of the complex coil data, $$$S_j$$$:
$$\boldsymbol\theta=\frac{\prod_{j\in M}|S_j|\exp\left(i\left(\sum_{j\in M}\phi_{j,rel}+M\phi_{common}\right)\right)}{\prod_{j\in M}|S_j|}$$
where $$$M$$$ is the set of coils without null points. This is a modified version of the sensitivity approximation proposed by Cao et al4. For a sufficiently large $$$M$$$, the phase of $$$\boldsymbol\theta$$$ is dominated by the common phase. Thus, to approximate the relative phase profile for a given coil, $$$\hat{\phi}_{j,rel}$$$, divide $$$S_j$$$ by $$$\boldsymbol\Theta$$$, where $$$\boldsymbol\Theta$$$ is calculated by unwrapping the phase of $$$\theta$$$ and dividing by $$$M$$$. The resultant estimates are smoothed to reduce the high noise levels in individual coil data. Then the background phase corrected data set, $$$\tilde{S_j}=\frac{S_j}{\exp\left(\hat{\phi}_{j,rel}\right)}$$$, is used to perform local coil compression3. We refer to this entire combination process as Corrected Local Coil Compression (C-LCC).
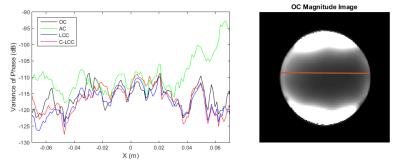
First we compared the combined phase profile from C-LCC, LCC, and AC to that of OC. Next we compared the combined phase data noise level for all four methods. The relative noise level was calculated as the standard deviation of the residual after fitting a 2nd order surface to the phase data over 7x7 pixel windows. Finally we compared the conductivity maps calculated from the phase data from each of the combination methods, using standard phase-based conductivity mapping5 followed by a 5x5 median filter. Results are presented for a uniform gel sphere and a volunteer subject’s brain, acquired on a GE 3.0T MRI scanner using a 32-channel NOVA Medical head coil. A 2D spin echo sequence was used with the following scan parameters: TE/TR = 16/1200 ms, FOV = 24x24x2.1 cm, 1.25x1.25x3.0 mm3 voxels. The subject was scanned under IRB approval.
Results
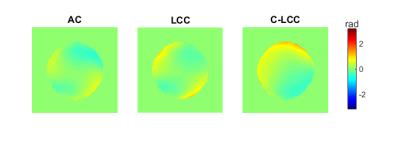
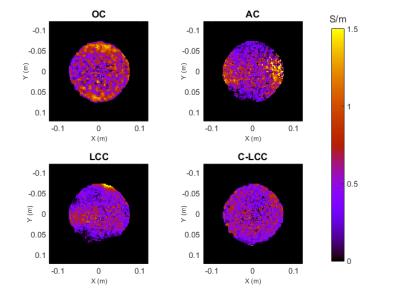
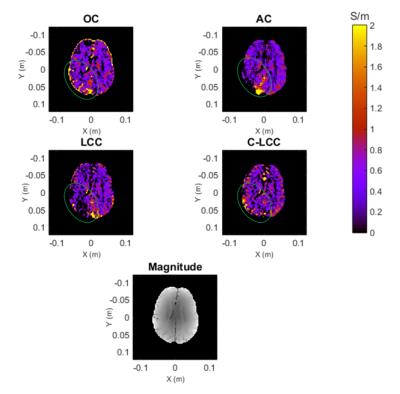
The proposed C-LCC method yields combined phase data with a different shape than AC and LCC, as shown in Figure 1. The absolute error with respect to OC is not lower, but the shape has a lower order representation and therefore introduces less bias into conductivity calculations. Furthermore, C-LCC phase data has lower noise than AC, but comparable noise to LCC and OC, as shown in Figure 2. Figure 3 shows that C-LCC gives the most uniform conductivity maps in a uniform phantom. In the human brain in Figure 4, we see better signal recovery from C-LCC than LCC and AC, particularly within the green ellipses.Discussion
Noise in the proposed method is related to the smoothing of the estimated relative spatial phase profiles, similar to estimating sensitivity maps for Optimal Combine. However, the proposed background phase removal reduces higher order bias in the combined phase data, producing more uniform conductivity maps in a uniform phantom and improving signal recovery in the human brain.Conclusions
We propose a data-driven approach to remove individual coil relative spatial phase contributions to reduce bias in the phase curvature when using local coil compression. This method allows for combination of multi-channel data for phase-based conductivity mapping with the SNR benefits of local coil compression and reduced bias from individual coil phases sensitivities.Acknowledgements
No acknowledgement found.References
[1] Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med 1990;16:192-225.
[2] Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 2000;43:682-690.
[3] Ropella KM, Noll DC. Coil Compression for Improved Phase Image Signal-to-Noise Ratio in Electrical Property Tomography. In Proceedings of the 24th Annual Meeting of the ISMRM, Singapore, 2016, p. 1564.
[4] Cao M, Stenger VA, Eddy W. Estimation of Images and Sensitivities for Multi-Coil MRI. In Proceedings of the 13th Annual Meeting of the ISMRM, Miami Beach, FL, USA, 2005, p. 2447.
[5] H. Wen. Non-invasive quantitative mapping of conductivity and dielectric distributions using the RF wave propagation effects in high field MRI. In Proceedings of SPIE: Medical Imaging; Physics of Medical Imaging. 2003; 5030:471-477.
Figures