3641

Dictionary-based Electric Properties Tomography
Ulrich Katscher1, Max Herrmann1, Christian Findeklee1, Mariya Doneva1, and Thomas Amthor1

1Philips Research Europe, Hamburg, Germany

Synopsis

Electric Properties Tomography (EPT) derives tissue conductivity and permittivity according to the Helmholtz equation via the second derivative of the measured complex B1 map, or by iteratively solving the corresponding forward problem. This abstract presents a different type of EPT reconstruction: the measured B1 map is compared locally with entries of a dictionary, which are small B1 maps of a priori known electric properties. This "dictionary-based EPT" (db-EPT) could be able to solve the transceive phase problem as well as the boundary problem of EPT. This study applies db-EPT to numerical and experimental data comparing different types of dictionaries.

Purpose

Electric conductivity and permittivity can be derived from a measured complex B1 map solving the Helmholtz equation ("Electric Properties Tomography", EPT [1]). Conventional EPT reconstruction methods suffer from two major issues [2]: the treatment of tissue boundaries, where conventional EPT reconstruction methods are prone to artefacts, and the required separation of transmit and receive components from the measured transceive phase. To handle these problems, this study investigates a new type of EPT reconstruction: the measured B1 map is compared locally with entries of a dictionary, which are small B1-maps of a priori known electric properties. This "dictionary-based EPT" (db-EPT) could be able to solve the transceive phase problem as well as the boundary problem of EPT.

Theory

The entries of the dictionary are small B1 patches (optionally in 1D, 2D, or 3D), which correspond to a priori known conductivity and permittivity. These patches are compared locally with patches of same size taken from the measured B1 map (as illustrated in Fig. 1). Conductivity and permittivity corresponding to the entry showing the best match with the measured patch are taken for reconstruction. For 1D patches ("strings"), matching is performed separately for each spatial direction corresponding to the three spatial derivatives of the Helmholtz equation, and the three values obtained are added to obtain the final electric properties. The strings can be based on uniform electric properties or two (or more) areas with discontinuous electric properties, thus representing tissue boundaries. Corresponding to the other types of EPT reconstruction techniques, entries can contain only B1 phase for (approximate) conductivity reconstruction, or only B1 magnitude for (approximate) permittivity reconstruction, or a complex B1 map for reconstructing both, conductivity and permittivity.

Methods

In this work, 1D entries of B1 phase φ with a length of 11 voxels with uniform electric properties are considered. Two studies are performed to investigate db-EPT.

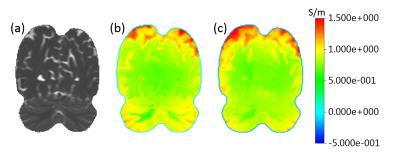
Study (A): The entries of the dictionary contain parabolic B1 phase strings φ(r) ~ a(r-b)2+c. Curvature a reflects the conductivity and b the off-center of the parabola, i.e., multiple strings with different b belong to the same curvature (conductivity). The offset c is fixed by subtracting the mean phase from the string, as it is done for the strings extracted from the measured B1 phase. The dictionary is built by 100 different values of a and 128 different values of b, thus 12800 entries in total. Using this parabola-based dictionary is similar to conventionally calculating the second derivative of the phase, and thus, is used to show the feasibility of the approach. It is applied to the brain of a healthy volunteer measured with a Steady-State-Free-Precession sequence (TR/TE=3.4/1.7ms; voxel=1×1×1 mm3; flip=25°, 3T Ingenia, Philips Healthcare, Best, Netherlands). The result is compared with a corresponding, conventional reconstruction using numerical differentiation. CPU time for both reconstructions is a few minutes using a 64-bit Intel processor (2.67 GHz, 12 GB RAM).

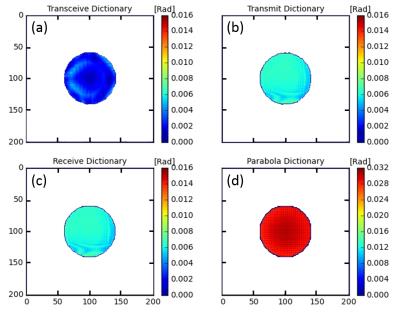
Study (B): Along with the parabolic dictionary of study (A), three different realistic dictionaries are created with the help of full electro-magnetic field simulations of homogeneous spheres with a diameter of 8 cm and a quadrature head coil (CONCEPT II, TU Hamburg-Harburg, Germany): dictionaries containing (i) phase of RF transmission (TX), (ii) phase of RF reception (RX), and (iii) transceive phase (superposition of TX and RX phase corresponding to the experimental situation). The dictionaries are applied to the transceive phase of a homogeneous sphere, and the matching errors of the different dictionaries are compared. This comparison is done to demonstrate that db-EPT is able to treat the measured transceive phase, and separating transceive phase into TX and RX phase is not needed.

Results

Study (A), Fig. 2: Reconstructed conductivity using parabola-based dictionary is close to conventionally reconstructed conductivity using numerical differentiation.

Study (B), Fig. 3: Matching error for reconstructing conductivity from transceive phase of homogeneous sphere is lowest using the transceive dictionary as expected. Matching errors using TX and RX dictionaries are very close as expected, but clearly higher than the matching error using the transceive dictionary. Matching error of parabola dictionary is clearly higher than all three realistic dictionaries.

Discussion / Conclusion

Study (A) confirms the feasibility of db-EPT. - The matching errors obtained in study (B) underline that db-EPT is able to handle the transceive phase, in contrast to conventional EPT. Furthermore, it is expected that db-EPT is able to solve the boundary problem by using entries including discontinuous electric properties, representing tissue boundaries. Thus, db-EPT might offer a superior alternative for reconstructing electric properties from B1 maps.

Acknowledgements

No acknowledgement found.

References

[1] Haacke EM et al., Extraction of conductivity and permittivity using magnetic resonance imaging, Phys Med Biol 36 (1991) 723

[2] Katscher U et al., Recent Progress and Future Challenges in MR Electric Properties Tomography, Comput Math Methods Med 2013:546562

[3] Katscher U et al., Towards the investigation of breast tumor malignancy via electric conductivity measurement, ISMRM 21 (2013) 3372

Figures

Fig. 1: Illustrating dictionary-based EPT exemplarily for phase-based conductivity reconstruction. Left: string of measured phase (extracted from full 3D phase map). Center column: Phase distributions ("strings") of three different, exemplary dictionary entries. Right column: conductivity distributions underlying the phase distributions in the column on the right. The phase string of entry (b) (middle row) shows best match with measured phase string, and thus, conductivity (b) is chosen for reconstruction.

Fig. 2: Brain study of healthy volunteer. (a) SSFP magnitude image, (b) conductivity obtained from conventional reconstruction applying numerical second derivative, (c) conductivity obtained from dictionary-based reconstruction with parabolic entries. The high similarity of the two conductivity maps (b,c) underlines the feasibility of dictionary-based EPT (both conductivity maps are median filtered according to [3]).

Fig. 3: Matching error for simulated sphere with conductivity = 0.5 S/m, relative permittivity = 65 (axes in mm). (a) Using the transceive dictionary (iii) yields the lowest matching error. (b,c) Using the transmit dictionary (i) yields nearly the same matching error as using the receive dictionary (ii) as expected from symmetry; however, this error is 2-3 times higher than the error from transceive dictionary. (d) Using the parabola dictionary yields a matching error which is roughly 10 times higher than the error from transceive dictionary (please note different color scale used for (d)).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3641