3640
CONtrast Conformed Electrical Properties Tomography (CONCEPT) based on Multi-channel Transmission1Department of Biomedical Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Institute for Engineering in Medicine, University of Minnesota, Minneapolis, MN, United States
Synopsis
Magnetic Resonance based Electrical Properties Tomography holds promise to provide valuable information on tissue functional changes, such as Tumorigenesis. We propose a novel technique based on
Purpose
Electrical Properties Tomography (EPT) offers a unique perspective into local tissue function and pathological condition. It has great potential for various biomedical applications, such as cancer diagnosis1 and SAR estimation2. However, conventional reconstruction methods rely on strong assumptions regarding subject anatomy to tackle the otherwise ill-posed inverse problem, such as symmetry and local tissue homogeneity3. These assumptions substantially compromise its generality and reliability. Here we propose a novel technique based on multi-channel RF transmission, dubbed CONtrast Conformed Electrical Properties Tomography (CONCEPT), which reconstructs sparse electrical properties images informed by the spatial variation of this very contrast.Theory
By fitting to Maxwell’s Equations with measured transmit $$$B_1$$$ magnitude and relative phase distributions using a multi-channel transmission array, two pieces of the puzzle can be retrieved: Firstly, the absolute transmit phase distribution of each channel encoding absolute electrical properties information; Secondly, the spatial variation of electrical properties describing the contrast between tissues4. The former can be decoded to obtain quantitative electrical properties by solving a linear inverse problem $$$E\gamma=C$$$, where $$$\gamma=\frac{1}{\epsilon-i\sigma/\omega}$$$, $$$\epsilon$$$ being permittivity, $$$\sigma$$$ conductivity and $$$\omega$$$ operating angular frequency5–7. The latter is used to generate a binary mask $$$W$$$ that differentiates between transition zone ($$$W=1$$$) and homogeneous area ($$$W=0$$$) for distinguished regularization strategies. In the transition zone, the first norm of electrical properties variation is constrained to promote clearer boundary, whereas the second norm is minimized in the homogeneous area to alleviate oscillating artifacts. The resultant convex optimization problem in its Lagrangian form reads as:$$\min_\gamma\:\|E\gamma-C\|_2^2+\lambda_1W\|\triangledown\gamma\|_1+\lambda_2\overline{W}\|\triangledown\gamma\|_2^2$$ The resultant $$$\gamma$$$ is a complex-valued quantity from which conductivity and permittivity can be derived using its definition equation.Methods
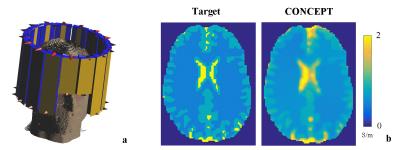
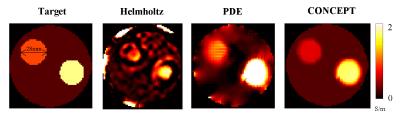
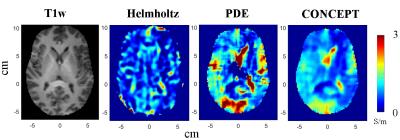
Simulations: A 16-channel microstrip coil array for brain imaging was numerically reproduced in SEMCAD, loaded with: (1) Cylindrical digital phantom (long axis 21cm, short axis 17cm, length 16cm) with 2cm-diameter tube anomalies spanning conductivity of 0.5-2.0S/m and permittivity of 35-85$$$\epsilon_0$$$; (2) Realistic 3D Duke head model. Electromagnetic field simulation was performed at 298 MHz. Complex $$$B_1^+$$$ from each channel was obtained and interpolated onto 1.5mm Cartesian grid. The relative phase and magnitude of $$$B_1^+$$$ were used for image reconstruction. Experiments: A 12cm-diameter three-compartment agar phantom was constructed with conductivity probed as 0.244S/m, 0.952S/m and 1.761S/m, respectively. A 16-channel microstrip coil array was used to measure $$$B_1^+$$$ magnitude and relative phase at the resolution of 1.5x1.5x1.5mm3 using the hybrid $$$B_1$$$ mapping method at Siemens 7T MRI8,9. A similar experimental setup was used to image the brain of a healthy human subject. Image Reconstruction: Least-squares fitting was performed to retrieve the spatial variation of electrical properties contrast and absolute transmit phase distribution. A binary mask $$$W$$$ was generated by hard-thresholding the former so that ~30% of the pixels in the region of interest were identified as transition zone. Alternating Direction Method of Multipliers (ADMM)10 was implemented in MATLAB to solve the optimization problem with a fixed iteration number of 60.Results
Simulations: Fig. 1c shows comparison of reconstruction results using the simulated phantom. CONCEPT correctly reproduces the original contrasts with substantially alleviated boundary and oscillation artifacts. The smallest differences between the base and anomalies are 0.25S/m for conductivity and 3$$$\epsilon_0$$$ for permittivity, which are preserved during the reconstruction. The optimization problem is solved in 2.5 seconds on a desktop PC. Fig. 2b demonstrates its ability to reconstruct complex brain structures using a 3D head model. Experiments: Fig. 3 and 4 present results from phantom and brain scans, respectively. CONCEPT demonstrates higher resistance to noise contamination and $$$B_1$$$ bias in both cases, with clear delineation of the conductivity contrast.Discussion
Previous studies on MR-based Electromagnetic properties mapping have demonstrated improved stability and accuracy when taking morphological images as a priori to regularize the central image reconstruction problem. Nevertheless, the morphological images contain mixed contrasts (T1, T2, proton density, etc.) which do not necessarily coincide with Electromagnetic ones11-13. This mismatch could lead to biased results or under-/over- regularization, manifesting as inaccurate result or artifacts. The proposed CONCEPT technique exploits the intermediate electrical properties contrast variation itself as constrains so as to bypass those potential pitfalls. Future development of this technique includes advanced design of the weighting mask and utilizing Total Generalized Variation to alleviate staircase artifact.Conclusion
Multi-transmission based CONCEPT is proposed and validated, demonstrating high accuracy and improved visual outcome. It does not make assumptions on anatomical symmetry or subjective “seed points”, therefore represents a general approach for both brain and body imaging.Acknowledgements
NIH R21 EB017069, R01 AT009263, R01 EB021027, R01 NS096761, P30 NS076408, P41EB015894 and S10RR026783 of WM KECK Foundation. We thank Dr. Mehmet Akcakaya, Dr. Jiaen Liu, Dr. Xiaotong Zhang and Mr. Long Yu for useful discussions.References
1. Tha KK, Katscher U, Yamaguchi S, Terasaka S, Toru Yamamoto T, Kudo K and Shirato H. Electrical Conductivity Characteristics of Glioma: Noninvasive Assessment by MRI and Its Validity. In: Proc. Intl. Soc. Mag. Reson. Med. 24, Singapore, 2016, p. 0274.
2. Zhang X, Schmitter S, Van de Moortele P, Liu J, He B. From Complex Mapping to Local SAR Estimation for Human Brain MR Imaging Using Multi-Channel Transceiver Coil at 7T. IEEE Trans. Med. Imaging 2013;32:1058–1067. doi: 10.1109/TMI.2013.2251653.
3. Zhang X, Liu J, He B. Magnetic-Resonance-Based Electrical Properties Tomography: A Review. Biomed. Eng. IEEE Rev. In 2014;7:87–96. doi: 10.1109/RBME.2013.2297206.
4. Liu J, Zhang X, Schmitter S, Van de Moortele P-F, He B. Gradient-based electrical properties tomography (gEPT): A robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging. Magn. Reson. Med. 2015;74:634–646. doi: 10.1002/mrm.25434.
5. Hafalir FS, Oran OF, Gurler N, Ider YZ. Convection-Reaction Equation Based Magnetic Resonance Electrical Properties Tomography (cr-MREPT). IEEE Trans. Med. Imaging 2014;33:777–793. doi: 10.1109/TMI.2013.2296715.
6. Wang Y, Zhang X, Liu J, Van de Moortele P-F, He B. Total Variance Constrained Electrical Properties Tomography Using a 16-channel Transceiver Array Coil at 7T. In: Proc. Intl. Soc. Mag. Reson. Med. 23, Toronto, Canada; 2015, p. 0195.
7. Liu J, Wang Y, Zhang X, Van de Moortele P-F, He B. PDE Solution of Electrical Properties Tomography With Multi-channel B1 Transmission. In: Proc. Intl. Soc. Mag. Reson. Med. 23, Toronto, Canada; 2015, p. 3300.
8. Adriany G, Van de Moortele P-F, Ritter J, Moeller S, Auerbach EJ, Akgün C, Snyder CJ, Vaughan T, Ugurbil K. A geometrically adjustable 16-channel transmit/receive transmission line array for improved RF efficiency and parallel imaging performance at 7 Tesla. Magn. Reson. Med. 2008;59:590–597. doi: 10.1002/mrm.21488.
9. Van de Moortele P-F, Snyder C, DelaBarre L, Adriany G, Vaughan T, Ugurbil K. Calibration tools for RF shim at very high field with multiple element RF coils: from ultra fast local relative phase to absolute magnitude B1+ mapping.
10. Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found Trends Mach Learn 2011;3:1–122. doi: 10.1561/2200000016.
11. Liu J, Liu T, de Rochefort L, et al. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. NeuroImage 2012;59:2560–2568. doi: 10.1016/j.neuroimage.2011.08.082.
12. Ropella K, Noll D. A Regularized Model-Based Approach to Phase-Based Conductivity Mapping. In: Proc. Intl. Soc. Mag. Reson. Med. 23, Toronto, Canada; 2015, p. 3295.
13. Katscher U., Gagiyev M, and Meineke J. Conductivity Determination of Deep Gray Matter Nuclei Utilizing Susceptibility-Based Delineation. In: Proc. Intl. Soc. Mag. Reson. Med. 24, Singapore, 2016, p. 3336.
Figures