3634

A Spatio-temporal Denoising Approach based on Total Variation Regularization for Arterial Spin Labeling
Cagdas Ulas1,2, Stephan Kaczmarz3, Christine Preibisch3, Jonathan I. Sperl2, Marion I. Menzel2, Axel Haase4, and Bjoern H. Menze1

1Department of Computer Science, Technische Universität München, Munich, Germany, 2GE Global Research, Munich, Germany, 3Department of Neuroradiology, Technische Universität München, Munich, Germany, 4Zentralinstitut für Medizintechnik, Technische Universität München, Munich, Germany

Synopsis

We present a new spatio-temporal denoising method for arterial spin labelling MR image repetitions, and mainly aim to improve the quality of perfusion-weighted images and cerebral blood flow (CBF) maps obtained from a subset of all dynamics available. Our technique is based on a two-step 3D total variation regularization, which is applied to subsets of control/label pairs in the first step and to resulting perfusion-weighted (difference) images in the second step. We demonstrate that our method leads to improved quality of perfusion-weighted images and CBF maps compared to existing spatial filtering techniques in short computation time.

Purpose

Arterial spin labeling (ASL) perfusion MRI is a non-invasive imaging technique that allows to quantify signals correlated to the cerebral blood flow (CBF) by magnetically labeling the arterial blood water1. While ASL has great potential to accurately reflect the cerebral perfusion, the low signal-to-noise (SNR) in ASL requires repeating the acquisitions numerous times to improve the signal reliability by averaging all the repetitions, which leads to clinically prolonged scanning times2. One possibility for overcoming this limitation is to reduce the spatial or temporal noise by applying various filtering techniques3,4. Unlike the previous methods, this work aims at exploiting simultaneously the local (voxel-wise) information of control/label (C/L) pairs and of their subtracted signals based on 3D total variation (TV).

Methods

The denoising approach presented here consists of a two-step optimization problem. In the first step, we apply the TV regularization jointly to C/L pairs to enforce voxel-wise (local) consistency within C/L dynamics. This problem is formulated as follows, $$\{\hat{x}_{C},\hat{x}_{L}\}=\underset{x_{C}, x_{L}}{\text{min}} \quad \|\mathcal{E}(x_{C})-I_{C}\|_2^2+\|\mathcal{E}(x_{L})-I_{L}\|_2^2+\lambda_1 TV(x_{C})+\lambda_2 TV(x_{L})$$ where $$$I_{C}$$$ and $$$I_{L}$$$ are available 3D C/L volume dynamics for denoising, which constitute a 4D data matrix, $$$\mathcal{E}$$$ is an expanding operator that generates a number of copies of 3D volumes along temporal dimension, $$$\lambda_1$$$ and $$$\lambda_2$$$ are two tuning parameters. The TV term is based on voxel-wise finite differences along spatial x, y, z dimensions, and can be defined as, $$TV(X)=\sum_{i,j,k}\sqrt{\sum\limits_{d=1}^{3} \left(\nabla_d \left(X_{i,j,k}\right)\right)^2}$$ where $$$\nabla_d$$$ is the forward finite difference operator along dimension $$$d$$$. As output of the first step, we obtain TV-regularized single control and label images, $$$\{\hat{x}_{C},\hat{x}_{L} \} $$$. Their subtraction yields a perfusion weighted image, $$$d=\hat{x}_{L}-\hat{x}_{C}$$$. In the second step, we apply TV regularization on the resulting perfusion-weighted images to preserve spatial edges while removing noise within homogeneous regions by minimizing voxel-wise intensity differences. This problem is formulated as, $$\Delta \hat{M}= \underset{\Delta M}{\text{min}} \quad \|\Delta M-\Delta M_0\|_2^2+\lambda_3 TV(\Delta M)$$ where $$$\Delta M_0$$$ is an initial difference image, set as $$$\Delta M_0=d$$$, and $$$\lambda_3$$$ is another tuning parameter. To solve aforementioned minimization problems, we employ an accelerated iterative algorithm5 based on the FISTA framework for TV regularization. Pseudo-continuous ASL (pCASL) images were acquired from 5 healthy subjects at a 3T Philips Ingenia MR scanner using acquisition parameters of 2D EPI readout, voxel size=$$$2.7\times2.7\times5$$$ mm$$$^3$$$, matrix size=$$$128\times128$$$, 17 slices, TR/TE=5000/14.6 ms, flip angle=90$$$^{\circ}$$$, labelling duration=1800 ms, post-label delay (PLD) =1604 ms. 30 C/L pairs and one M0 image were acquired for each subject. All ASL data preprocessing steps (motion correction, co-registration, smoothing) were applied on C/L pairs using our in-house ASL toolbox. For comparison, we also employed two previously proposed spatial filtering techniques for ASL: Adaptive Wiener4 and Independent Component Analysis (ICA) based filter4. Optimal results were achieved for each method by empirically tuning required model parameters (see Table 1). Contrast-to-noise ratio (CNR) is used for quantitative evaluation. CNR is determined between grey matter (GM) as tissue of interest and white matter (WM) as background.

Results

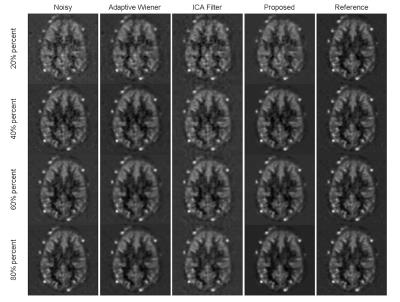
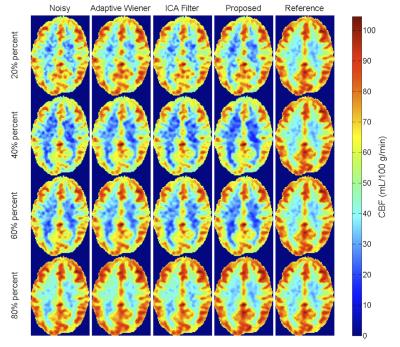
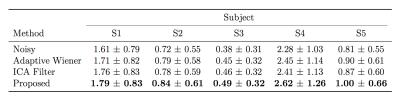
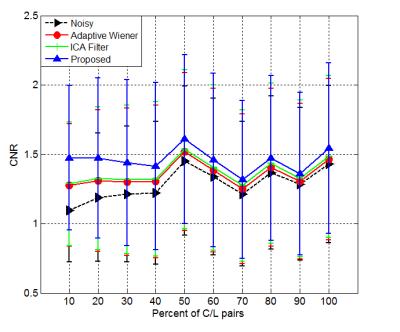
Figures 1 and 2 display the perfusion-weighted ($$$\Delta M$$$) images and CBF maps, respectively, and demonstrate the comparison of the results depending on various percentage of C/L pairs used. Our method yields higher quality images and CBF maps with better GM/WM contrast. Finer image details are mostly preserved and sharpened compared to the two spatial filtering techniques. The Adaptive Wiener filter produces blurry regions in CBF maps and ICA filter results in less blurry regions but leads to missing details. Table 2 shows the quantitative comparison (in terms of CNR) of different methods for all subject data, where our proposed method achieves the best CNR. Figure 3 illustrates the improved performance of our method with respect to different percentages of C/L pairs. All filtering methods lead to higher improvements in CNR when only less than half of the repetitions used.

Discussion

Our main finding is that the voxel-wise spatial differences of temporal C/L pairs can be exploited to improve the quality of perfusion-weighted images obtained by averaging less repetitions than acquired. This study reveals that in our data sample, which consists of 30 C/L pairs, at least 40-50% of the repetitions are required in order to obtain clinically acceptable perfusion maps. The quality of resulting noisy maps can be further improved with the proposed method. Our denoising method is computationally very efficient and takes around 5-20 seconds (on a Intel desktop) depending on the percentage of C/L pairs used in denoising procedure. Therefore, it can be easily integrated into any ASL post-processing pipeline. Future work will aim at investigating the possibility of accelerating ASL in multi-PLD acquisitions using our method.

Acknowledgements

The research leading to these results has received funding from the European Union’s H2020 Framework Programme (H2020-MSCA-ITN-2014) under grant agreement no 642685 MacSeNet.

References

1. Alsop D.C. et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn. Reson. Med. (2015).

2. Bibic, A. et al. Denoising of arterial spin labeling data: wavelet-domain filtering compared with Gaussian smoothing. Magnetic Resonance Materials in Physics, Biology and Medicine (2010).

3. Mumford J.A. et al. Estimation efficiency and statistical power in arterial spin labelling fMRI. Neuroimage (2006).

4. Well, J.A et al. Reduction of Errors in ASL Cerebral Perfusion and Arterial Transit Time Maps Using Image Denoising. Magn. Reson. Med. (2010).

5. Fang, R. et al. Robust Low-dose CT Perfusion Deconvolution via Tensor Total-Variation Regularization. IEEE Trans. on Med. Imag. (2015).

Figures

Table 1. Optimal model parameters empirically chosen for each denoising method. These parameter values were used for all subject’s data. For ICA Filter and Proposed method, the parameters take values from the given interval depending on the percent of C/L pairs used in denoising.

Figure 1. Reference (obtained by averaging all 30 C/L pairs) and the filtered perfusion-weighted images using various percentages of C/L pairs of Subject 1. Our proposed method produces maps with sharper image details and higher GM/WM contrast compared to other filtering methods. For this subject, 20% of the C/L pairs were not enough to capture all the perfusion-related information. To obtain relatively accurate perfusion maps, at least 40% percent of the data were required, but noisy maps can be further improved with our denoising method.

Figure 2. Reference CBF maps and filtered CBF maps obtained with the use of various percentages of C/L pairs of Subject 4. A brain mask is applied to CBF maps to remove noise outside the brain. Compared to unfiltered maps, our method produces higher quality maps with sharpened finer details. The Adaptive Wiener filter yields more blurry maps. ICA Filter results in relatively better maps, but the edges are preserved less compared to our technique.

Table 2. Contrast-to-noise ratio (CNR) values (mean±std) for all subjects obtained from different denoising methods when only 40% of C/L pairs are used. The mean and standard deviations are estimated using all 17 slices of our datasets. Our proposed method achieves the best CNR for all subjects (highlighted in bold).

Figure 3. Contrast-to-noise ratio (CNR) values of images with respect to percentage of C/L pairs used in denoising. The mean and standard deviations are estimated using all the subject’s data and slices. For every percentage of pairs, our method achieves the best average CNR among all methods. Interestingly, the CNR value of noisy images does not monotonically increase when a higher number of pairs is used in averaging. This implies that while background noise is reduced with averaging of more pairs, the mean signal difference between GM and WM may also decrease due to randomly occurring perfusion signals and noise.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3634