Synopsis

This study presents a comparative analysis of different reconstruction techniques for quantification of 3D maps of the cerebral metabolic rate of oxygen consumption (CMRO₂) in human brain. CMRO₂ maps were calculated from a direct ¹⁷O-MRI experiment at 3T in which ¹⁷O gas was inhaled. Conventional Kaiser-Bessel reconstruction of ¹⁷O MR images was compared to two iterative reconstruction methods using total variation (TV) and anisotropic diffusion (AD) of coregistered proton data as constraints. AD-constraint reconstruction, which acts as a non‑homogeneous edge‑preserving smoothing filter, enabled CMRO₂ mapping at clinical field strengths by increasing the SNR, and reducing partial volume effects.

Introduction

Oxygen metabolism is altered in brain tumors and neurodegenerative diseases, and can be assessed by the cerebral metabolic rate of oxygen consumption (CMRO₂). CMRO₂ can be measured by either ¹⁵O-PET [1] or by direct ¹⁷O-MRI with administration of ¹⁷O-enriched gas [2–6]. Recently, we performed a profile likelihood (PL) analysis that shows that CMRO₂ can be reliably quantified with ¹⁷O-MRI [6].

The purpose of this study was to enable 3D CMRO₂ quantification with ¹⁷O-MRI at 3T with partial volume effects (PVE) correction. Therefore, conventional Kaiser-Bessel (KB) gridding was compared to iterative reconstruction techniques with a total variation (TV) constraint and with a proton-based constraint using coregistered ¹H-MR data of higher spatial resolution as prior information. Here, an anisotropic diffusion (AD) metric of ¹H-MR data was used as an edge-preserving constraint [7]. Reconstructions were compared for numerical ¹⁷O‑MRI phantom and in vivo ¹⁷O‑MRI images and CMRO₂ maps.

Material and Methods

Direct 4D ¹⁷O-MR data of a male volunteer (50 years) were acquired with a 3D UTE density-adapted radial sequence [8] (nominal resolution Δx=10mm, temporal resolution Δt=1min) in an ¹⁷O-MRI inhalation experiment [6] (3L of 70%-enriched ¹⁷O gas; NUKEM Isotopes Imaging) at 3T (Siemens Magnetom TIM Trio) using a custom-built Tx/Rx ¹⁷O quadrature head coil.

For all ¹⁷O-MR phantom and in vivo images, KB gridding without/with Hanning filtering (KBwH/KBnH) was used. After gridding, the two iterative reconstructions were applied: TV-constraint and AD-constraint [7].

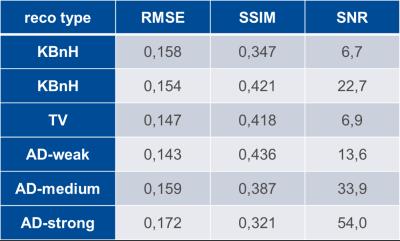
First, ¹⁷O MRI phantom images were reconstructed with different weighting factors for TV/AD constraints (λ_TV/λ_AD) over the range λ∈[10^-3…10^-5] to identify the values which give the best correspondence with the original phantom image. Therefore, root-mean-square error (RMSE) and structural similarity (SSIM, [9]), which is based on image luminance, contrast and structure comparison, were calculated. RMSE, SSIM, and SNR values, which were calculated by a pseudo-multiple-replica approach [10], were used for comparison of quality and precision of different reconstructions.

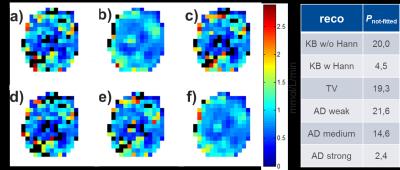
Second, optimized 𝜆 values were used to reconstruct in vivo ¹⁷O-MR images. 3D CMRO₂ maps were calculated for all reconstruction techniques from a realistic pharmacokinetic model with PL-based confidence intervals (CI) [6]. The percentage P of the pixels (P_not-fitted), for which CMRO₂ mapping failed due to low SNR, was then calculated.

Finally, CMRO₂ values and corresponding CIs calculated from the signal averaged over 10 pixels (V=10 ml) with GM/WM content higher than 73%/87% were used to quantify GM/WM tissue separation and PVEs correction.

Results and Discussion

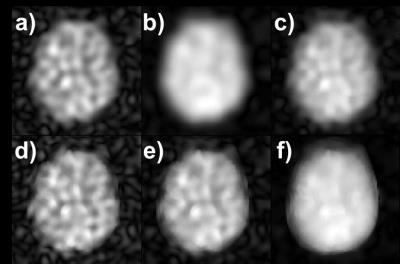
In the ¹⁷O-MRI phantom (Fig.1), KBwH led to increase in SSIM by 21% and in SNR by 338% (Tab.1) compared to KBnH, whereas TV-constrained reconstruction resulted in 7%/20% better RMSE/SSIM values, but did not substantially change SNR values. AD‑constrained reconstruction with λ=10, denoted by AD-weak, showed best correspondence with the original image (Fig. 1a) with 9%/26% improvement in RMSE/SSIM compared to KBnH. However, the SNR values were 40% lower compared to KBwH. Higher λ_AD values (λ_AD=50/100 denoted by AD-medium/strong) were also investigated and gave 49%/138% higher SNR, but a 3%/12% and 7%/24% worse RMSE and SSIM, compared to KBwH.

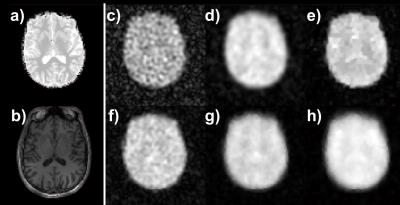
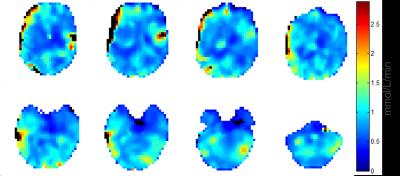
In vivo images reconstructed with different methods showed that KBwH and AD‑strong reconstruction (λ_AD=1000) yields a substantial SNR increase and made ventricles circumscribable (Fig. 2). With AD-strong reconstruction, fine GM structures could be seen. CMRO₂ maps of different reconstruction techniques showed that only AD-strong and KBwH reconstructions provide CMRO₂ maps with sufficient quality – the other methods had P_not‑fitted>14% (Fig. 3). AD‑strong had P_not-fitted=2.4%, which is 47% smaller then KBwH. CMRO₂ maps of AD-strong method interpolated to a larger matrix (Fig. 4), reveal CMRO₂ differences in various brain tissues: smaller CMRO₂ in WM and CSF regions compared to GM regions.

CMRO₂ values in small GM/WM regions were 0.82/0.76 µmol/g_tissue/min for KBwH and 0.84/0.74 µmol/g_tissue/min for AD-strong. GM and WM separation for AD-strong was 70% better compared to KBwH. PL-based CIs for the AD technique were 11/13% smaller compared to conventional reconstruction. Filtering among the neighboring pixels was beneficial: AD method smoothed data among pixels with similar intensity (mostly within one brain tissue component) and preserved borders within different tissue compartments (edge‑preservation), which is favorable compared to isotropic homogeneous Hanning filtering.

Conclusions and Outlook

Acknowledgements

References

[1] Leenders KL, Perani D, Lammertsma AA, Heather JD, Buckingham P, Healy MJ, Gibbs JM, Wise RJ, et al. Cerebral blood flow, blood volume and oxygen utilization. Normal values and effect of age. Brain 1990;113:27–47.

[2] Atkinson IC, Thulborn KR. Feasibility of mapping the tissue mass corrected bioscale of cerebral metabolic rate of oxygen consumption using 17-oxygen and 23-sodium MR imaging in a human brain at 9.4 T. Neuroimage 2010;51:723–733.

[3] Hoffmann SH, Begovatz P, Nagel AM, Umathum R, Schommer K, Bachert P, Bock M. A measurement setup for direct 17O MRI at 7 T. Magn. Reson. Med. 2011;66:1109–1115.

[4] Hoffmann SH, Radbruch A, Bock M, Semmler W, Nagel AM. Direct ¹⁷O MRI with partial volume correction: first experiences in a glioblastoma patient. MAGMA 2014;27:579–87.

[5] Borowiak R, Kurzhunov D, Wagner P, Reisert M, Bock M. Dynamic ¹⁷O-MRI at 3 Tesla for in vivo CMRO2 Quantification. In: In proceedings of 23rd Annual Meeting of ISMRM; Toronto, Canada. ; 2015. p. 4633.

[6] Kurzhunov D, Borowiak R, Hass H, Wagner P, Krafft AJ, Timmer J, Bock M. Quantification of oxygen metabolic rates in Human brain with dynamic ¹⁷O MRI: Profile likelihood analysis. Magn. Reson. Med. 2017

[7] Kurzhunov D, Borowiak R, Wagner P, Reisert M, Bock M. Proton-Constrained CMRO₂ Quantification with Direct ¹⁷O-MRI at 3 Tesla. In: In proceedings of 23rd annual meeting of ISMRM; Toronto, Ontario, Canada. ; 2015. p. 2450.

[8] Nagel AM, Laun FB, Weber M-A, Matthies C, Semmler W, Schad LR. Sodium MRI using a density-adapted 3D radial acquisition technique. Magn. Reson. Med. 2009;62:1565–1573.

[9] Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004;13:600–612.

[10] Robson PM, Grant AK, Madhuranthakam AJ, Lattanzi R, Sodickson DK, McKenzie C. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn. Reson. Med. 2008;60:895–907.

[11] Borowiak R, Groebner J, Haas M, Hennig J, Bock M. Direct cerebral and cardiac ¹⁷O-MRI at 3 Tesla: initial results at natural abundance. MAGMA 2014;27:95–99.