3521

Quantitative assessment of susceptibility artefact correction techniques for diffusion-weighted MRI

Mark S Graham¹, Ivana Drobnjak¹, and Hui Zhang¹

¹Centre for Medical Image Computing and Department of Computer Science, University College London, London, United Kingdom

Synopsis

It is necessary to correct for susceptibility artefacts in DW-MR, but there are a number of available strategies to choose from. In this work we apply a simulation framework, previously used to assess motion and eddy current correction strategies, to quantitatively evaluate methods for susceptibility correction. Our results indicate that methods that use reversed phase-encoding data perform the best. Furthermore they show that non-linear registration of diffusion data to a structural target in insufficient to fully correct for the susceptibility artefact.

Introduction

This work uses a simulation framework^1,2,3, previously applied to assess motion and eddy current correction strategies⁴, to quantitatively evaluate methods for correcting susceptibility artefacts in DW-MRI. These artefacts introduce geometric distortions that can prevent accurate alignment with structural images, adversely impact analysis such as tractography⁵, and increase variability in longitudinal or multicenter studies⁶. There are several strategies available to correct for these artefacts but there are no systematic, quantitative comparisons of these methods, which makes it difficult to know which should be employed. The choice of correction strategy is becoming increasingly important given that tradeoffs in cutting-edge multi-band protocols, such as the HCP⁷, have given rise to more pronounced susceptibility artefacts – something that is likely to ‘trickle down’ into more everyday acquisitions. In this work we apply the simulation framework to quantitatively evaluate the various strategies available for susceptibility correction.

Methods

Data: The simulation framework¹ was extended to include a spin-echo pulse sequence, enabling the simulation of DW-MR datasets with susceptibility artefacts. The simulated data consisted of 32 directions with b=1000s/mm², 4 b=0 images, TR/TE = 7500/109ms, dimensions 72/86/55 with voxel size 2.5mm³. Diffusion directions were distributed isotropically on the sphere. A susceptibility-induced off-resonance field was estimated using field-mapping data from the HCP project and used as a simulator input to produce susceptibility distorted data. The full dataset was simulated with phase encoding in both PA and AP directions, in addition to a ground truth dataset acquired without any susceptibility field. We also simulated a T2 structural image with 1.25mm³ resolution and a gradient-echo field mapping sequence.

Methods tested: We tested four strategies for susceptibility correction.

1) Non-linear registration of DW-MR data to a T2 structural image, constrained along the phase-encode direction, as implemented in NiftyReg⁸

2) Correction using a fieldmap estimated from a gradient-echo sequence, as implemented in FSL’s FUGUE.

3) Correction using a displacement field estimated from two b0 images with reversed phase-encoding (PE) as implemented in FSL’s TOPUP⁹.

4) Correction using a full dataset with reversed phase-encoding, in TOPUP. This allows for reconstruction of areas affected by compression, which methods 1-3 cannot offer.

Evaluation strategy: Assessment of susceptibility correction techniques is divided into three parts. Firstly, we assess the ability of each method to recover the correct underlying displacement field, by comparing each predicted field to the ground truth field used as an input to the simulator. Secondly, we assess the ability of each method to recover the correct intensity at each voxel by computing difference maps between the corrected and ground truth images. Finally we investigate the impact of correction quality on subsequent analysis by comparing diffusion tensor (DT) fits in both corrected datasets and ‘ground truth’ datasets, simulated free of artefacts.

Results

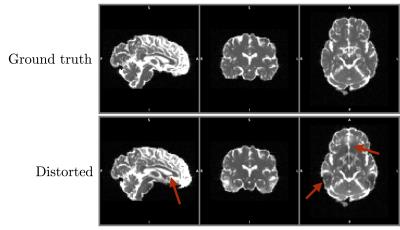
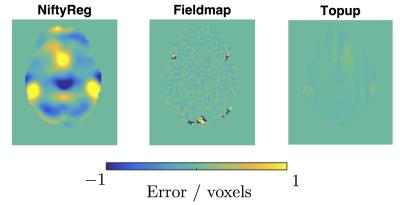
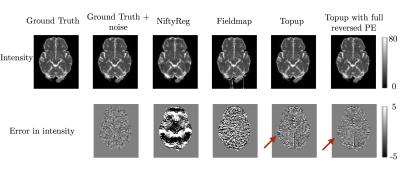
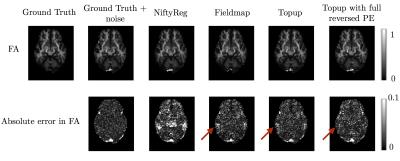
Example simulated data is shown in Figure 1. Displacement field errors for methods 1-3 are shown in Figure 2 (method 3 and 4 use the same displacement field, calculated just from the b=0 images with reversed phase encoding). The results show that registration between b=0 and structural is not able to recover the correct underlying displacement field in regions exhibiting susceptibility-induced pileup. Both field-mapping and reversed phase encoding methods accurately recovered the field. Figure 3 shows errors in the intensity of corrected images. Methods 1-3 should not be able to provide the correct intensity in regions of signal pile-up, even with the correct displacement field, while method 4 should be able to due to the extra information provided by the reversed PE images. This can be seen comparing e.g. methods 3 and 4 in Figure 3. This result is clearer when comparing DT metrics in Figure 4. Both methods 2 and 3 show errors in regions of signal compression that are reduced by method 4.

Discussion

Acquisition protocols such as the HCP project do not use in-plane acceleration⁷, which increases the severity of the susceptibility artefact. This protocol is becoming increasingly widely adopted and in these situations robust correction strategies are crucial. Our results indicate that optimal correction is achieved from acquiring the full datasets with reversed PE. Whilst our results showed similar performance of field-mapping or acquisition of a single image with reversed PE, we note that field-map based approaches are not able to correct for concomitant fields¹⁰ which were not included in our simulations, so we suggest a single reversed PE method in situations where a full reversed PE dataset cannot be acquired. Our findings are in agreement with previous simulation-based work¹¹, which used less direct measures to assess correction quality, as well as findings in real data¹².

Acknowledgements

MG is supported by the EPSRC (EP/L504889/1) and the EPSRC Centre for Doctoral Training (EP/L016478/1). HZ is supported by the EPSRC (EP/L022680/1), the MRC (MR/L011530/1) and the Royal Academy of Engineering Research Exchanges with China and India. ID is supported by the Leverhulme Trust.

References

[1] M.S Graham, I. Drobnjak, H. Zhang. Realistic simulation of artefacts in diffusion MRI for validation post-processing correction techniques. NeuroImage (2016) 125:1079–1094

[2] I Drobnjak, D Gavaghan, E Süli, J Pitt-Francis and M Jenkinson. Development of an FMRI Simulator for Modelling Realistic Rigid-Body Motion Artifacts. Magnetic Resonance in Medicine, 56(2), 364-380, 2006.

[3] I Drobnjak, G Pell and M Jenkinson. Simulating the effects of time-varying magnetic fields with a realistic simulated scanner. Magnetic Resonance Imaging, 28(7), 1014-21, 2010.

[4] M.S Graham, I. Drobnjak, H. Zhang. Quantitative evaluation of eddy-current and motion correction techniques for diffusion-weighted MRI, ISMRM 2016

[5] Lee J, Lazar M, Lee J, Holden J, Terasawa-Grilley E, Alexander AL. Correction of Bo EPI Distortions in Diffusion Tensor Imaging and White Matter Tractography. Proceedings of the 12th Annual Meeting ISMRM, Kyoto, Japan, 2004; 2172.

[6] Jones, D. K. (2012). Artifacts in Diffusion MRI.

[7] Sotiropoulos, Stamatios N., Saad Jbabdi, Junqian Xu, Jesper L. Andersson, Steen Moeller, Edward J. Auerbach, Matthew F. Glasser et al. "Advances in diffusion MRI acquisition and processing in the Human Connectome Project." Neuroimage 80 (2013): 125-143

[8] Modat, Marc, Gerard R. Ridgway, Zeike A. Taylor, Manja Lehmann, Josephine Barnes, David J. Hawkes, Nick C. Fox, and Sébastien Ourselin. "Fast free-form deformation using graphics processing units." Computer methods and programs in biomedicine 98, no. 3 (2010): 278-284.

[9] J.L.R. Andersson, S. Skare, J. Ashburner How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage, 20(2):870-888, 2003.

[10] Xiaohong Joe Zhou Ph.D. Yiping P. Du, Matt A. Bernstein, H. Glenn Reynolds, Joseph K. Maier, Jason A. Polzin Concomitant magnetic-field-induced artifacts in axial echo planar imaging

[11] Esteban, O., Daducci, A., Caruyer, E., O’Brien, K., Ledesma-Carbayo, M. J., Bach-Cuadra, M., & Santos, A. (2014). Simulation-based evaluation of susceptibility distortion correction methods in diffusion mri for connectivity analysis. 2014 IEEE 11th International Symposium on Biomedical Imaging, ISBI 2014, 738–741.

[12] Wu M, Chang L-C, Walker L, Lemaitre H, Barnett AS, Marenco S, Pierpaoli C (2008). Comparison of EPI distortion correction methods in diffusion tensor MRI using a novel framework. MICCAI Proceedings 2:321–329.

Figures

Figure 1. Comparison of simulated ground truth and distorted data, b=0 image shown, phase-encoding direction is AP. Compared to the ground truth, the distorted data shows signal pileup above the ear canals and roof of the mouth, as well as elongation of the frontal region of the brain, including the corpus callosum.

Figure 2. Errors in the displacement field predicted by three methods, shown across one axial slice of the brain.

Figure 3. One axial slice of the ground truth and corrected images shown, as well as error maps obtained by subtracting the ground truth intensity. Arrows indicate a region where intensity is only fully corrected when using the full reversed phase encoding dataset.

Figure 4. FA values across one slice of the brain for ground truth and corrected data. Bottom row shows error maps. Arrows indicate regions where methods that are unable to recover the correct intensity distribution lead to high errors.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3521