3518
Accelerating Diffusion Tensor Imaging Using a Parametric Manifold Model1Electrical Engineering, University at Buffalo,State University of New York, Buffalo, NY, United States, 2Radiology, Johns Hopkins University School of Medicine, Baltimore, MD, United States, 3Radiology, New York University School of Medicine, New York City, NY, United States, 4Biomedical and Health Engineering, Shenzhen Institutes of Advanced Technology, Shenzhen, People's Republic of China, 5Electrical & Computer Engineering, University of Utah, Salt Lake City, UT, United States, 6Biomedical Engineering, University at Buffalo, State University at New York, Buffalo, NY, United States
Synopsis
This abstract presents a novel method for diffusion tensor image (DTI) directly from highly under-sampled data acquired at multiple diffusion gradients. This method formulates the diffusion tensor estimation as a problem of parametric manifold recovery. We solve the recovery problem by alternatively shrinking the diffusion weighted images, estimating diffusion tensor, and enforcing data consistency constraint. The experimental results demonstrate that the proposed method is able to reconstruct the diffusion tensors accurately at high acceleration factors with low computational complexity.
Purpose
Diffusion tensor imaging(DTI)[1] provides important information on brain microstructure and connectivity, but it suffers from lengthy acquisition time, especially when acquired at high resolution. Several compressed-sensing(CS) based[2-9] methods and fast sequences[10] have been developed to reduce the acquisition time. However, most CS-based methods are demanding in computation time. In this paper, we propose a novel and computationally efficient method to reconstruct the diffusion tensors directly from the highly undersampled k-space data. The proposed method alternately shrinks the images in wavelet space, projects onto the parametric manifold with the diffusion tensor model, and enforces data consistency.Method
Theory: In DTI, the m-th diffusion-weighted image $$${I_m}$$$ can be written as: $${I_m}={I_0}{e^{- bg_m^TD{g_m}}},\quad(1)$$where $$${I_0}$$$ is the reference non-diffusion weighted image, b is diffusion weighting factor, $$${g_m}$$$ is the m-th normalized diffusion gradient vector, and the diffusion tensor D is a 3 × 3 symmetric matrix. It can be seen that regardless the large number of diffusion-weighted images with different diffusion gradient directions, all these images lie on a low dimensional manifold whose dimension depends only on the six degrees of freedom in D. We therefore are able to recover the diffusion tensor D directly from the under-sample k-space $$${d_m}$$$ acquired at all diffusion gradients, which is related to the diffusion-weighted image Im as:$${d_m}={F_m}{I_m}+{n_m},\quad(2)$$where $$${F_m}$$$ is the Fourier operator with a specific under-sampling pattern at m-th acquisition, $$${n_m}$$$ denotes noise. We formulate the estimation of the diffusion tensor D as following minimization problem:$${\bf{D}}:= arg\mathop{\min}\limits_{\bf{D}}\mathop\sum\limits_m\left|{\left|{{d_m}-{F_m}{I_0}{e^{-bg_m^T{\bf{D}}{g_m}}}}\right|}\right|_2^2,\quad(3)$$To solve such a non-convex minimization problem, we first initialize $$${I_m}$$$ by performing a zero-filled Fourier reconstruction. We then alternate among the following three steps iteratively.
Step1:Shrinkage-thresholding: We first use a soft-thresholding function to update each individual DWI in wavelet domain:$${\hat I_m}=Shrink\left({W\left({{I_m}}\right),\lambda}\right)\buildrel\Delta\over=\left\{{\begin{array}{*{20}{c}}{W({I_m}) -\lambda,}&{\begin{array}{*{20}{c}}{if}&{W({I_m})>\lambda}\end{array}}\\{0,}&{else}\end{array}}\right.,\quad(4)$$here Shrink(.) is the soft-thresholding function and λ is the threshold.
Step2:Diffusion tensor estimation by projecting DWIs onto the parametric manifold model: The updated images from the first step $$$\hat{I}_{m}$$$ is used here to estimate the diffusion tensor D, which can be easily solved by the least squares method:$${\bf{D}} = {\rm{arg}}\mathop {\min }\limits_{\bf{D}} \mathop \sum \limits_m \left\| {\ln {I_0} - {\rm{ln}}{{\hat I}_m} - bg_m^T{\bf{D}}{g_m}} \right\|_2^2,\quad(5)$$
Step3:Projection onto the subspace with data consistency: The images are further transformed into k-space to enforce the data consistency constraint. Specifically the values at unacquired k-space locations are replaced by updated values in step 2 while the values at acquired k-space locations are maintained. These three steps are performed iteratively until convergence.
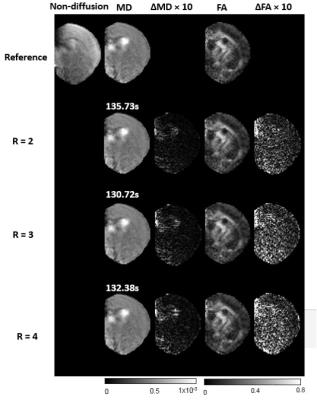
MRI: The proposed method was evaluated using a mice brain DTI dataset (n=5) acquired using a horizontal 11.7T MR scanner as described in [11]. The data were acquired using a 3D GRASE sequence with selective excitation pulses and the following parameters: TE/TR=21/1000msec, two signal averages; spectral width = 120kHz; Four non-diffusion weighted images and sixty diffusion-weighted images (b=2500s/mm2, resolution=0.1mm isotropic, matrix size = 92 × 54). The fully sampled k-space data was retrospectively under-sampled with reduction factors of 2,3 and 4 using different 2D random under-sampling patterns for different diffusion directions. Mean diffusivity (MD) and fractional anisotropy (FA) maps were used to evaluate the performance.
Results & Discussion
Figure 1 compares the MD and FA maps retrospectively reconstructed with different reduction factors against the maps from the full acquisition. The results suggest that the proposed method can reconstruct the MD and FA maps with no apparent artifacts at reduction factors up to 4. Both the differences in MD and FA maps showed relatively small increases in estimation errors near the base of the brain, which had lower SNR than the top of the brain (closer to the receive-only coil). In contrast to the existing methods, where the diffusion tensor is estimated by solving a complicated optimization problem, the proposed method enforces wavelet sparsity constraint in the spatial domain of DWIs, projects the DWIs to its closet parametric manifold, and enforces data consistency alternatively. As aresult, each step only requires some simple computation and the iterations converge fast. With a MATLAB implementation on a PC with 2.39GHz Intel Xeon CPU and 10.0GB RAM, the proposed method takes about 2minutes to reconstruct the DTI in 3D, which is much faster than the method in [8].Conclusion
In this abstract, we propose a novel method to accelerate diffusion tensor imaging. The experimental results demonstrate the proposed method is able to accurately recover MD and FA maps from highly accelerated acquisition.Acknowledgements
This work is supported in part by the NSF CCF-1514403, NIH R21 EB020861, R21 NS098018, and NIH R01HD074593.References
[1] P.J. Basser, J. Mattiello, D. Lebihan, "MR diffusion tensor spectroscopy and imaging," Biophys J 66, 259-267 (1994).
[2] H. Gao, L. Li, K. Zhang, W. Zhou, X. Hu, "PCLR: phase-constrained low-rank model for compressive diffusion-weighted MRI," Magn Reson Med 72, 1330-1341 (2014).
[3] D. McClymont, I. Teh, H.J. Whittington, V. Grau, J.E. Schneider, "Prospective acceleration of diffusion tensor imaging with compressed sensing using adaptive dictionaries," Magn Reson Med 76, 248-258 (2016).
[4] Y. Jiang, E.W. Hsu, "Accelerating MR diffusion tensor imaging via filtered reduced-encoding projection-reconstruction," Magn Reson Med 53, 93-102 (2005).
[5] Y. Wu, Y.J. Zhu, Q.Y. Tang, C. Zou, W. Liu, R.B. Dai, X. Liu, E.X. Wu, L. Ying, D. Liang, "Accelerated MR diffusion tensor imaging using distributed compressed sensing," Magn Reson Med 71, 763-772 (2014).
[6] X. Shi, X. Ma, W. Wu, F. Huang, C. Yuan, H. Guo, "Parallel imaging and compressed sensing combined framework for accelerating high-resolution diffusion tensor imaging using inter-image correlation," Magn Reson Med 73, 1775-1785 (2015).
[7] L.L. Pu, T.P. Trouard, L. Ryan, C. Huang, M.I. Altbach, A. Bilgin, "Model-Based Compressive Diffusion Tensor Imaging," 2011 8th Ieee International Symposium on Biomedical Imaging: From Nano to Macro, 254-257 (2011).
[8] C.L. Welsh, E.V. DiBella, G. Adluru, E.W Hsu " Model-Based Reconstruction of Undersampled diffusion tensor k-space data", Magn Reson Med 70:429-440 (2013).
[9] Y.J. Zhu, Y. Wu, Y.J. Zheng, E.X. Wu, L. Ying, D. Liang, "A Model-Based Method with Joint Sparsity Constraint for Direct Diffusion Tensor Estimation," 2012 9th IEEE International Symposium on Biomedical Imaging, 510-513 (2012).
[10] Y. Cai, M.S. McMurray, I. Oguz, H. Yuan, M.A. Styner, W. Lin, J.M. Johns, H. An, "Use of High Resolution 3D Diffusion Tensor Imaging to Study Brain White Matter Development in Live Neonatal Rats," Front Psychiatry 2, 54 (2011).
[11] D. Wu, D. Reisinger,J. Xu,S.A. Fatemi, van Zijl, P. C. M.Peter, Mori, S.,J.Y. Zhang, Localized diffusion magnetic resonance micro-imaging of the live mouse brain. NeuroImage, 91, 12–20(2014).