3514
Accelerated Body nCPMG SS-FSE Diffusion Weighted Imaging1Department of Bioengineering, Stanford University, Stanford, CA, United States, 2Praecedentia Libra, Palaiseau, France, 3Department of Radiology, Stanford University, Stanford, CA, United States, 4Department of Electrical Engineering, Stanford University, Stanford, CA, United States
Synopsis
This abstract presents a novel reconstruction for the nCPMG SS-FSE sequence. A theoretical justification for this approach is given. This reconstruction and sequence is demonstrated in phantom and in vivo and is shown to be quantitatively and qualitatively robust.
Introduction
SS-FSE is a fast and robust method to acquire images in a single shot in regions of $$$B_0$$$ inhomogeneity without image distortion. SS-FSE sequences rely on a rigid phase modulation throughout the echo train known as CPMG. Because of these phase requirements, many contrast preparations (e.g., diffusion weighting) are typically unsuited for use in SS-FSE. Various methods have been proposed to work around the loss of the CPMG condition [1][2][3][4] though each comes with drawbacks in terms of SNR, motion from a multi-shot acquisitions, or a complicated reconstruction scheme. The nCPMG phase modulation approach[4] leads to a (1, -1, 1, -1…) amplitude modulation on the quadrature component of the signal and thus aliasing. This can be represented as [5]
$$Q_n = (A+b)X + (-1)^n (A-b)Y,$$
where $$$Q_n$$$ is the image signal at each n echo, $$$X$$$ is the in phase component of the image, and $$$Y$$$ is the out of phase component of the image. The coefficients $$$A$$$ and $$$b$$$ are complex valued and are slowly varying in the spatial domain if nutation angle is controlled[5]. We propose modifying the nCPMG SS-FSE sequence to include an accelerated self-calibrated reconstruction for body DWI applications.
Methods
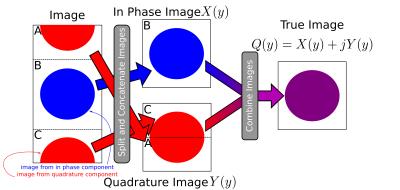
The proposed reconstruction doubles the field of view by oversampling in k-space by a factor of 2 in a nCPMG sequence (Fig. 1). This necessarily doubles the number of phase encodes. From there the object can be reconstructed by taking the top quarter and bottom quarter of the image to generate the $$$Y$$$ component of the image. The center of the image can extracted to find $$$X$$$. Thus, the final image is found by combining
$$Q = X + jY$$
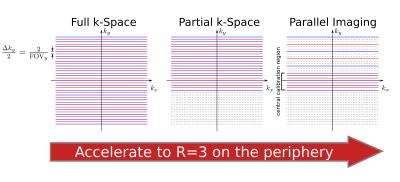
after appropriate corrections to account for the $$$(A+b)$$$ and $$$(A-b)$$$ phase terms. Fig. 2 shows this procedure. Double phase encoding does lead to increased SAR, TE, as well as phase encode direction blur. These effects can be ameliorated by using a partial k-space reconstruction (which also corrects for the phase errors introduced by the coefficients $$$A$$$ and $$$b$$$) as well as parallel imaging. Here, partial k-space is used combined with uniform sampling with $$$R=3$$$ in the periphery (Fig. 3). Reconstruction is performed via the ESPIRiT algorithm. Agar ball phantom and in vivo images were acquired using a 32-channel head and body coils, respectively, on a GE 3T scanner. FOV varied from 20cm to 40cm, matrix size 192x128, TR=600ms, TE=65ms, and b=700s/mm2. In vivo images are pediatric abdominal cases. All in vivo images were scanned in the coronal plane to best match the coil sensitivity patterns.
Results
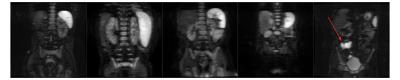
Phantom nCPMG SS-FSE DWI images (Fig. 4) show consistent contrast throughout the phantom. The associated phantom image shows similar consistency. The mean ADC value for the SS-FSE case is 0.00184 mm/s2. For comparison, an EPI phantom ADC is also provided. The mean ADC value for the EPI case was 0.00183 mm/s2. In vivo images (Fig 5.) show similar contrast between each case. The nCPMG SS-FSE images do not show image distortion and signal dropouts that are often seen in EPI images. In case 5, a mesenteric nodal metastasis is spotted by the right hip (denoted by a red arrow).Conclusion
We have developed an accelerated and self-calibrating algorithm for nCPMG SS-FSE acquisitions. We have demonstrated this sequence and reconstruction in phantom and in vivo. We have seen that this approach does work as expected in terms of distortion and contrast. The integrity of this method is further demonstrated by the matching ADC values between the EPI and SS-FSE phantom values.Acknowledgements
The authors would like acknowledge funding from NSF DGE-1147470, NIH P41 EB015891, NIH R01 EB009690, as well as GE Healthcare.References
[1] Alsop, David C. "Phase insensitive preparation of single-shot RARE: Application to diffusion imaging in humans." Magnetic Resonance in Medicine 38.4 (1997): 527-533.
[2] Pipe, James G., Victoria G. Farthing, and Kirsten P. Forbes. "Multishot diffusion-weighted FSE using PROPELLER MRI." Magnetic Resonance in Medicine 47.1 (2002): 42-52.
[3] Deng, Jie, Reed A. Omary, and Andrew C. Larson. "Multishot diffusion-weighted SPLICE PROPELLER MRI of the abdomen." Magnetic Resonance in Medicine 59.5 (2008): 947-953.
[4] Le Roux, Patrick. "Non-CPMG fast spin echo with full signal." Journal of Magnetic Resonance 155.2 (2002): 278-292.
[5] Gibbons, Eric, et al. "Body diffusion weighted imaging using non-CPMG fast spin echo." IEEE Transactions on Medical Imaging (2016).
Figures