3512

Accelerated High Resolution EPI DTI Using Model-Based Reconstruction
Zijing Dong1, Fuyixue Wang1,2, Zhe Zhang1, Erpeng Dai1, Xiaodong Ma1, Yuantao Gu3, and Hua Guo1

1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, People's Republic of China, 2Harvard-MIT Health Sciences and Technology, MIT, Cambridge, MA, United States, 3Department of Electronic Engineering, Tsinghua University, Beijing, People's Republic of China

Synopsis

Single-shot EPI is the most widely used sequence in diffusion tensor imaging. However, severe distortion in single-shot EPI limits its application for higher resolution images. Multi-shot EPI DTI can reduce distortion but results in longer acquisition time especially when a large number of diffusion-encoding directions are used. Here, we propose a model-based reconstruction framework for EPI DTI to estimate diffusion tensors from undersampled EPI sequences, in order to achieve high resolution diffusion imaging in a shorter scan time. The effectiveness of the proposed model-based method to get precise tensor estimation is validated by DTI simulation and in-vivo experiments.

Purpose

Distortion in single-shot EPI caused by low bandwidth along the phase encoding direction impedes high resolution diffusion imaging. Partially sampling k-space using parallel imaging (PI) 1, 2 can reduce the distortion, however, it suffers SNR penalty. Another way to get high resolution DTI is using multi-shot EPI techniques combined with phase correction methods 3-5. However, it can lead to long acquisition time especially when multiple diffusion-encoding directions are used. Recently, a model-based reconstruction combined with compressed sensing (CS) for diffusion imaging has been developed for 3D and radial spin-echo DTI acceleration 6, 7. Here, we propose a novel model-based reconstruction framework for multishot EPI DTI, which can directly estimate the diffusion tensors from undersampled k-space data to accelerate the acquisition.

Methods

If a Gaussian model for diffusion is assumed, the k-space signal of DTI can be represented by:$$K_{i,k}(D)=\sum_{j=1}^{N_{s}}e^{-i\overrightarrow{k_{i}}\overrightarrow{x_{j}}}(f_{x_{j}}p_{x_{j},k})e^{-B_{k}D_{x_{j}}}$$

where $$$f_{x_{j}}$$$ is the magnitude of non-diffusion-weighted (b0) image at location $$$\overrightarrow{x_{j}}$$$. The diffusion weighted image along the $$$k$$$-th diffusion-encoding direction can be represented by multiplying the b0 image with $$$p_{x_{j},k}$$$, the phase of the corresponding diffusion image, and exponential attenuation $$$e^{-B_{k}D_{x_{j}}}$$$, where $$$D$$$ is the diffusion tensor and $$$B$$$ is the b-matrix. $$$\sum_{j=1}^{N_{s}}e^{-i\overrightarrow{k_{i}}\overrightarrow{x_{j}}}$$$ is the Fourier Transform operator and $$$K_{i,k}$$$ represents the k-space data at the $$$i$$$-th point.

In the proposed model-based reconstruction, image phase of each direction and each shot can be estimated using PI-based methods or 2D navigators, and $$$f$$$ is fully sampled. Thus, diffusion tensor $$$D$$$ is the only unknown in this equation if data $$$K$$$ is given. To estimate the diffusion tensor, we use the following object function with the input of undersampled k-space data:

$$arg\min \limits_{D} \frac{1}{2}\lVert\tilde{K}-K(D)\rVert_2^2+\lambda\lVert TV(D)\rVert_1$$

Here, the first term is data fidelity and the second term is total variation (TV). $$$\tilde{K}$$$ is the acquired undersampled k-space data. $$$K(D)$$$ is the k-space data calculated by Equation 1 using the estimated $$$D$$$. $$$\lambda$$$ is a parameter to control the contribution of TV. To solve this optimization problem, a nonlinear conjugate gradient algorithm is adopted. Figure 1 illustrates the estimation process.

Simulation: To evaluate the proposed method quantitatively, DTI datasets were simulated. A diffusion scan was performed to calculate a set of diffusion tensors $$$D$$$ as the golden standard. Non-diffusion weighted images were duplicated and multiplied by the exponential attenuation term using tensor $$$D$$$ to generate multi-direction diffusion-encoded images. Then, spatially varying random phases (2nd-order) were applied to the images and Gaussian noise was added in k-space (SNR = 5). Finally, the simulated k-space data were uniformly undersampled with predefined acceleration factors (AF). In the first simulation, 12-direction and 32-direction DTI data were simulated with different AFs. The performance of the proposed method was compared with SENSE 1 and PI+CS method L1-SPIRiT 8. In the second simulation, 12-direction DTI data with different partial Fourier factors were simulated to evaluate the combination of model-based reconstruction and partial Fourier acquisition.

In-vivo experiment: In vivo DTI data were acquired using an interleaved 4-shot EPI sequence with navigators on a Philips 3T Achieva TX scanner. The scan parameters were: number of RF channels = 8, FOV = 220×220 mm2, slice thickness = 4 mm, TR/TE = 3500/83 ms, in-plane image resolution = 1×1 mm2, number of diffusion directions = 10, b value = 1000 s/mm2, NSA = 2, partial Fourier factor = 0.75. The proposed method and L1-SPIRiT reconstructed images with using the image echo of one shot along each direction to achieve an AF of 4 (two shots with AF = 2). The fully sampled 4-shot data were reconstructed using a multi-shot GRAPPA method 5 as a reference.

Results

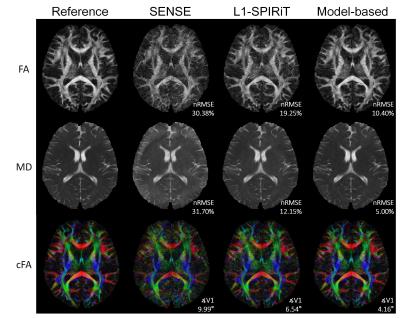
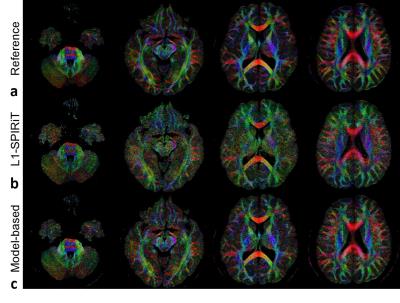
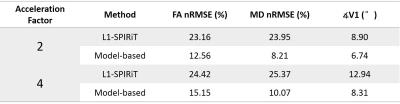
Figure 2 shows the images reconstructed by the three methods in the first simulation. The proposed model-based method gave the lowest errors in the three parameters evaluated. At different AFs with 12 or 32 directions, the proposed method also achieved FA with lower errors (Figure 3a). The results of partial Fourier test were shown in Figure 3b. The proposed method performed better with different partial Fourier factors than L1-SPIRiT. Figure 4 shows the reconstructed color-coded FA (cFA) maps in the in-vivo experiment, and more quantitative results are shown in Table 1, which demonstrates improved image quality and accuracy of the proposed method.

Discussion and Conclusion

The proposed model-based reconstruction can directly estimate the tensors using undersampled k-space data to achieve high resolution EPI DTI with shorter scan time while maintaining accuracy. The superior performance to traditional PI and PI+CS methods as well as the compatibility with partial Fourier acquisition has been preliminarily demonstrated. The combination of model-based reconstruction with SMS acquisition can achieve further acceleration.

Acknowledgements

This work was supported by Tsinghua University Initiative Scientific Research Program.

References

1. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med, 1999. 42(5): p. 952-62.

2. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med, 2002. 47(6): p. 1202-1210.

3. Zhang Z, Huang F, Ma X, Xie S, Guo H. Self-feeding MUSE: a robust method for high resolution diffusion imaging using interleaved EPI. Neuroimage, 2015. 105: p. 552-60.

4. Porter, D. and E. Mueller. Multi-shot diffusion-weighted EPI with readout mosaic segmentation and 2D navigator correction. In Proc Intl Soc Mag Reson Med. 2004.

5. Ma X, Zhang Z, Dai E, Guo H. Improved multi-shot diffusion imaging using GRAPPA with a compact kernel. Neuroimage, 2016.

6. Knoll F, Raya JG, Halloran RO, Baete S, Sigmund E, Bammer R, Block T, Otazo R, Sodickson DK. A model-based reconstruction for undersampled radial spin-echo DTI with variational penalties on the diffusion tensor. NMR Biomed, 2015. 28(3): p. 353-66.

7. Welsh CL, Dibella EV, Adluru G, Hsu EW. Model-based reconstruction of undersampled diffusion tensor k-space data. Magn Reson Med, 2013. 70(2): p. 429-40.

8. Lustig M, Alley M, Vasanawala S, Donoho D, Pauly J. L1 SPIR-iT: autocalibrating parallel imaging compressed sensing. In Proc Intl Soc Mag Reson Med. 2009.

Figures

Figure 1. The schematic illustration of the proposed model-based reconstruction framework. First, the image phase is estimated using GRAPPA from undersampled k-space data. Then DW images can be calculated by multiplying the fully sampled b0 image with filtered phase and diffusion-induced exponential term. The estimated tensor D with total variation constraint contributes to the exponential term calculation. The data fidelity is performed between the k-space of estimated DWI and acquired one. To achieve a precise estimation of D, a non-linear conjugate gradient algorithm is implemented based on the model with data fidelity and total variation constraint.

Figure 2. Results of the first simulation using 32-direction DTI data at an AF of 4. Three parameters, nRMSE of fractional anisotropy (FA), nRMSE of mean diffusivity (MD) and the angular deviation of the principal eigenvector V1, were calculated. The proposed model-based method shows the lowest error. In addition, the proposed method provided results closer to the reference.

Figure 3. a: The mean error of FA reconstructed by the three methods in the first simulation. DTI data with 12 and 32 directions were simulated with various acceleration factors. The error of the proposed method using 12-direction DTI data at AF = 4 is even smaller than the other two methods at AF= 2 using the same number of directions, and it is also smaller than them using 32-direction data at AF of 4. b: The mean error of FA from L1-SPIRiT and the proposed method using 12-direction DTI data at AF = 4 with different partial Fourier factors.

Figure 4. Color-coded FA maps reconstructed by (a) multi-shot GRAPPA using fully sampled data, (b) L1-SPIRiT at AF = 4 (only one of four shots was used) and (c) the proposed model-based reconstruction method at AF = 4 of the in-vivo DTI experiment. A 4-shot interleaved 10-direction data were used with NSA = 2. The images reconstructed by proposed method have less noise than L1-SPIRiT and are closer to the reference.

Table. 1. Three quantitative parameters for evaluating the estimated tensors in the in-vivo experiment. Acceleration factor = 2 was achieved by using two of four shots and AF = 4 was using only one shot of four. The deviations from the proposed method are much lower than L1-SPIRiT.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3512