Synopsis

For joint k-q reconstruction, it’s beneficial to incoherently under-sampling k-space for different q-space points to utilize the complimentary k-space information. As nearby q-space points in general share more similarities than distant points, it is hypothesized that locally-incoherent k-space sampling can further improve the joint k-q reconstruction. In this work, we propose a method to design locally-incoherent k-space sampling patterns based on a graph colouring algorithm. Results show the proposed method achieves better reconstruction than existing sampling schemes.

Purpose

Introduction

Recently, several diffusion MRI studies have demonstrated improved reconstruction of under-sampled k-space data by exploring the data redundancy in q-space using a joint k-q reconstruction^1-5. A common finding is that by acquiring k-space incoherently for different q-space points, the missed k-space lines can be better recovered using the complimentary k-space information from all q-space points. Different k-space under-sampling strategies have been proposed, including random sampling³ and circulant sampling^1,2,4,5.

These methods increase the global incoherence of k-space under-sampling, but do not specifically aim to achieve local incoherence. Nearby q-space points generally share more common features (i.e. the images are more similar) than distant points. We therefore hypothesize we can improve joint k-q reconstruction by incoherently under-sampling k-space within local q-space neighborhoods. In this work, we propose a graph model approach to design locally incoherent k-space under-sampling and evaluate its efficacy using a newly proposed k-q reconstruction algorithm based on Gaussian processes (presented in another abstracted by our group).

Methods

For EPI with an under-sampling factor of R, there exist R unique sampling patterns (produced by shifting the under-sampled trajectory along the phase-encoding direction) that can be applied at different q-space points. Random sampling of k-space as widely used for compressed sensing is not compatible with EPI; instead, we randomize the distribution of under-sampled EPI across different q-space locations to achieve (global) incoherence.

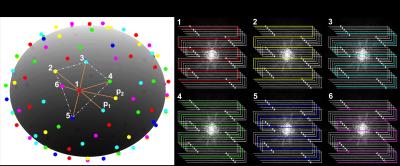
Achieving local incoherence requires a more sophisticated design approach than either randomized or circulant sampling. For each q-space point, a neighborhood is defined including itself and its R-1 nearest neighbors (measured by angular distance). To maximize the local incoherence of k-space under-sampling patterns, it is desirable to assign circulant k-space sampling patterns within each q-space neighborhood (Fig.1). This can be equivalently described as a graph-coloring problem, where each q-space point corresponds to a vertex and an edge between two vertices exists if the corresponding two q-space points are within the same neighborhood. If the constructed graph can be colored using R different colors while obeying that no connected vertexes share the same color, the resultant coloring scheme provides locally-incoherent k-space sampling.

Graph coloring is an “NP-complete” problem, which means no efficient algorithms are available that provide the exact optimal solution. We applied a greedy algorithm⁶ to approximate the solution. However, for high reduction factors (highly-connected graph), the greedy algorithm fails to find a solution. To alleviate the problem, the size of neighborhood was slightly reduced when constructing the graph.

A joint k-q reconstruction algorithm utilizing sharable information in q-space based on Gaussian processes was used to evaluate the proposed sampling scheme. This approach builds a statistical model for the joint distribution of different data points and predicts the missing k-space data in a given q-space point from adjacent locations. A simulated 8-channel diffusion data set (normally wouldn’t support parallel imaging with R>4) with 128 directions and b=1000 s/mm² were used in the reconstruction. Randomly generated linear phase maps were added to different diffusion directions to simulate motion-induced phase errors. In-plane reduction factor of 6 was tested. For comparison, three other sampling schemes were also evaluated, including using the fixed sampling pattern (a conventional diffusion acquisition); randomized sampling; and circulant sampling pattern along a ‘smooth’ q-space trajectory⁵.

Results

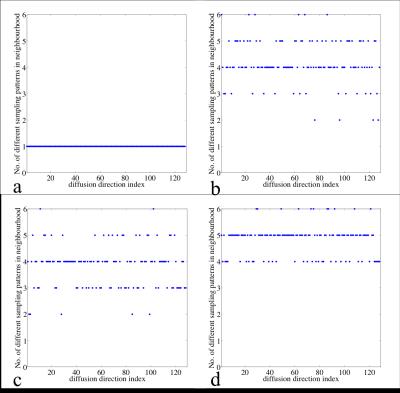
To measure the performance of the sampling scheme, a local incoherence metric Ns is defined as the number of different k-space sampling patterns within each R-neighborhood in q-space. Using smooth circulant sampling (Fig.2b) or randomized sampling scheme (Fig.2c), the global incoherence of k-space sampling is improved, but suffers at some q-space points with low Ns of 2 or 3. With the proposed method, the local incoherence of k-space sampling is improved with no q-space points having Ns<4.

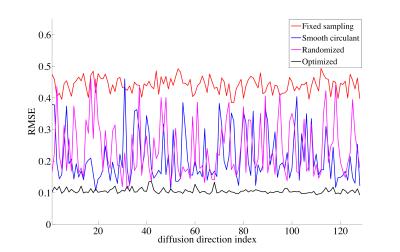
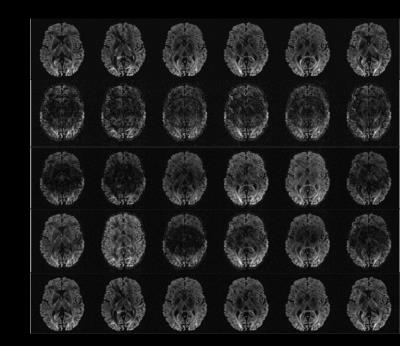
Fig.3 compares the RMSE of reconstructions from different sampling schemes. Using the fixed sampling pattern leads to the highest reconstruction errors, which is expected as no complementary k-space information can be used. With smooth-circulant or randomized sampling, the reconstructions are improved for some directions but fail for many others. Using the optimized sampling scheme, the reconstructions for all directions are improved. Fig.4 shows the reconstructions of the first 6 diffusion directions, clearly demonstrating image artefacts.

Discussion and conclusion

We present a method to improve joint k-q reconstruction by incoherently under-sampling k-space data within local q-space neighborhoods using a graph-coloring algorithm. Reconstructions based on a newly developed algorithm demonstrate superior performance over other sampling designs. The proposed sampling scheme hasn’t been evaluated using alternate joint k-q reconstruction methods, which will be investigated in the future.

Acknowledgements

References

1. Madore B, Chiou JYG, Chu R, Chao TC, Maier SE. Accelerated multi-shot diffusion imaging. Magnetic Resonance in Medicine 2014;72:324-336.

2. Gao H, Li L, Zhang K, Zhou W, Hu X. PCLR: Phase-constrained low-rank model for compressive diffusion-weighted MRI. Magnetic Resonance in Medicine 2014;72:1330-1341.

3. Mani M, Jacob M, Guidon A, Magnotta V, Zhong J. Acceleration of high angular and spatial resolution diffusion imaging using compressed sensing with multichannel spiral data. Magnetic Resonance in Medicine 2015;73:126-138.

4. Shi X, Ma X, Wu W, Huang F, Yuan C, Guo H. Parallel imaging and compressed sensing combined framework for accelerating high-resolution diffusion tensor imaging using inter-image correlation. Magnetic Resonance in Medicine 2015;73:1775-1785.

5. Chao T-C, Chiou J-yG, Maier SE, Madore B. Fast diffusion imaging with high angular resolution. Magnetic Resonance in Medicine 2016; doi: 10.1002/mrm.26163.

6. D. J. A. Welsh and M. B. Powell An upper bound for the chromatic number of a graph and its application to timetabling problems. Comput. J. 10 (1967), 85–86.