3503

Whole-brain diffusional variance decomposition (DIVIDE) in 8 minutes: Technical feasibility at 1.5, 3, and 7 T
Filip Szczepankiewicz1, Jens Sjölund2,3,4, Freddy Ståhlberg1,5,6, Jimmy Lätt7, and Markus Nilsson5,6

1Medical Radiation Physics, Lund University, Lund, Sweden, 2Elekta Instrument AB, Kungstensgatan 18, Box 7593, SE-103 93 Stockholm, Stockholm, Sweden, 3Department of Biomedical Engineering, Linköping University, Linköping, Sweden, 4Center for Medical Image Science and Visualization, Linköping University, Linköping, Sweden, 5Department of Clinical Sciences Lund, Lund University, Skåne University Hospital, Lund, Sweden, 6Lund University Bioimaging Center, Lund University, Lund, Sweden, 7Department of Imaging and Function, Skåne University Hospital, Lund, Sweden

Synopsis

Diffusion weighting along more than one direction at a time (tensor-valued encoding) can be used to probe features of the microstructure that are not accessible by conventional encoding. For example, it enables diffusional variance decomposition (DIVIDE) which can separate the effects of microscopic anisotropy, orientation dispersion, and heterogeneous isotropic diffusivity. Tensor-valued encoding is usually demanding with respect to gradient performance, limiting its applicability to high-performance MRI systems. However, a recent method for optimized encoding significantly reduced the demand on gradient performance, which warrants an investigation of the applicability of such encoding on a wider range of MRI hardware configurations. In this study, we demonstrate whole-brain diffusional variance decomposition (DIVIDE) in less than 8 minutes at a wide range of clinical MRI systems with different hardware configurations.

Purpose

Diffusional variance decomposition (DIVIDE) is a method that enables estimation of the microscopic diffusion anisotropy independent of orientation coherence1,2, and it can distinguish between disordered eccentric cells and variable cell density3—features which are conflated by methods that use only conventional (linear) diffusion encoding4, such as DTI5 or DKI6. The DIVIDE method is based on b-tensors with multiple eigenvalue configurations, or shapes (rank 1–3). Rank 2 encoding is enabled by double diffusion encoding, but arbitrary shapes can be rendered by q-space trajectory encoding (QTE)2,7. However, QTE usually requires strong gradients to render feasible echo times, which has previously restricted its implementation to high-performance systems.

Recent development of optimized QTE8 has motivated its implementation at a wider range of MRI systems. The purpose of this study was therefore to investigate the feasibility of whole-brain DIVIDE based on QTE at a wide range of clinical MRI systems.

Methods

We performed QTE at three MRI systems (A-C, Table 1) in a single healthy volunteer (male, 35 y). Hardware specifications and the 8-minute imaging protocols are shown in Table 1. Asymmetric waveforms8 that yield linear and spherical b-tensors (LTE and STE) were tailored for each system independently. Images were corrected for motion and eddy-currents9,10. Smoothing was avoided to retain the effect of noise.The signal model was based on the gamma distribution function, which was fitted to the powder averaged signal to estimate the mean diffusivity (MD) and the isotropic and anisotropic diffusional variance (VI and VA)2,3. The diffusional variance components (or mean kurtosis6 components) were scaled and normalized, according to

$$\text{MK}_x=3\frac{{V_x}}{\text{MD}^2}$$

where ‘x’ denotes the specific component (MKT=MKI+MKA)3. The µFA was defined as2,3,7

$$\text{µFA}=\sqrt{\frac{3}{2}}\left( 1+ \frac{ \text{MD}^2+V_I}{5/2 \cdot V_A} \right)^{-1/2}$$

We note that MKI reflects the heterogeneity of isotropic diffusivities, whereas MKA and µFA reflect the diffusion anisotropy on the microscopic level (µFA can be interpreted as the FA that would be observed if all structures were ordered in parallel)2,3,7. The SNR=E[S(b)]/σ[S(b)] was calculated from multiple repetitions of the STE. A metric of quality (Q3) was computed from the fractional volume of the brain parenchyma where SNR>3 (cf. ref. 11) at b=2000 s/mm2, excluding regions where MD<1.5 µm2/ms. We consider the quality of data to be sufficient if Q3≥95%. We also investigated if the high performance of system B afforded 2 mm isotropic voxels. A whole-brain volume was acquired at a resolution of 2×2×2 mm3 in 9 min by using only b=100, 1000, and 2000 s/mm2 in 6, 10, and 16 directions at TR=8400 ms.

Results

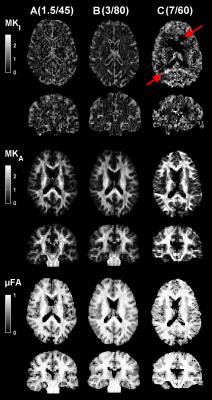
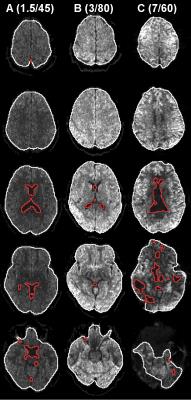
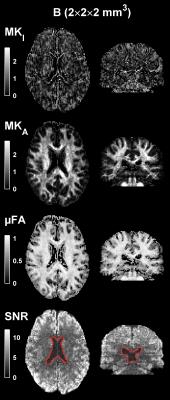
Figs. 1 and 2 show parameter and SNR maps at all systems. At system A the SNR was lowest, but still sufficient (Q3=97%), although the MKI map was visibly affected by noise. System B showed the best image quality and highest SNR (Q3=100%). System C exhibited slightly different parameter contrast and was also noticeably affected by image artifacts. The SNR at system C was sufficient at Q3=95%, but only after regions of gross signal loss due to RF inhomogeneity were excluded. Fig. 3 shows parameter and SNR maps at system B with 2 mm isotropic voxels. The smaller voxels rendered a lower SNR and an appreciable effect of noise in the MKI map, however, the SNR remained sufficient (Q3=98%). Generally, the MKA and µFA appeared to be less affected by noise than MKI.

Discussion and conclusions

We have demonstrated that whole-brain DIVIDE based on QTE is feasible at a wide range of MRI systems, and shown examples of the parameter maps that can be expected at acquisition times of 8 minutes. The feasibility hinges on optimized asymmetric waveforms; these reduce the echo times by ≈ 40% vs. previous implementation1,3, which increases SNR by a factor 2–3 (T2 times from ref. 12). Furthermore, we achieved 2 mm isotropic voxels at system B, which is an unprecedented spatial resolution in the context of b-tensor encoding.

Notably, this study cannot account for different RF systems, reconstruction, post-processing etc. This is most relevant at 7 T where improved RF homogeneity and fat suppression will likely improve the results. Furthermore, the proposed protocols are adapted to the brain, and may require modifications if applied to other tissues.

In conclusion, whole-brain DIVIDE is technically feasible in 8 minutes at main magnetic fields between 1.5 and 7 T, and gradient amplitudes as low as 43 mT/m. This demonstration may incite the investigation of relatively unexplored features, such as the microscopic diffusion anisotropy and the components of diffusional variance, on a wider range of systems.

Acknowledgements

We thank Philips Healthcare and Siemens Healthcare for providing sequence code and access to the pulse programming environments.

References

1. Szczepankiewicz et al., Neuroimage 104, 241-252 (2015); 2. Lasic et al. Frontiers in Physics 2, 11 (2014); 3. Szczepankiewicz et al. Neuroimage (2016); 4. Mitra, Physical Review B 51 (21), 15074-15078 (1995); 5. Basser et al. Biophys. J. 66 (1), 259-267 (1994); 6. Jensen et al. Magn. Reson. Med. 53 (6), 1432-1440 (2005); 7. Westin et al. Neuroimage 135, 345-362 (2016); 8. Sjölund et al. J. Magn. Reson. 261, 157-168 (2015); 9. Klein et al. IEEE Trans. Med. Imaging 29 (1), 196-205 (2010); 10. Nilsson et al. PLoS ONE 10 (10), e0141825 (2015); 11. Gudbjartsson and S. Patz, Magn. Reson. Imaging 34 (6), 910-914 (1995); 12. Cox and Gowland, Magn. Reson. Med. 64 (5), 1440-1445 (2010); 13. Szczepankiewicz et al. Proc. Intl. Soc. Mag. Reson. Med. 24, 2065 (2016).

Figures

Fig. 1 | Parameter maps in transversal and coronal slices at three MRI systems (A-C, see Table 1) in one healthy volunteer. Parentheses show B0 and Gmax in units of T and mT/m. Generally, the image quality improves with field strength and gradient amplitude. At system C, two notable artifacts appeared (red arrows); the anterior region exhibited negative MKI possibly due to poor RF homogeneity, and in the posterior region we observed a prominent fat artifact. Furthermore, system E generally exhibited higher values of MKA and µFA compared to the other systems.

Fig. 2 | SNR maps at b=2000 s/mm2 in five transversal slices, calculated from data acquired MRI systems A-C in one healthy volunteer. Red outlines show regions where SNR<3; white outlines show the outer bound where SNR>3. On systems A and B the SNR was only low in regions that contain cerebrospinal fluid. Generally, the SNR was lower in the central and inferior parts of the brain. The irregular brain outline at system C was likely caused by poor RF homogeneity; as indicated by the white outline, some of these regions were not included in the quality metric (Q3).

Fig. 3 | Parameter and SNR maps in transversal and coronal planes in a healthy brain at a resolution of 2×2×2 mm3. The high spatial resolution lowered the SNR compared to the default resolution of 2×2×4 mm3, however, the SNR remained sufficient at Q3=98%.

Table 1 | Hardware specification and imaging protocols. All systems used matrix 256×256×30, resolution 2×2×4 mm3, partial Fourier 0.75, acceleration factor 2, bandwidth 1400 Hz/voxel, min/max b-values 100/2000 s/mm2. The echo and repetition time determined the number of samples b-shells13. Equal number of linear and spherical b-tensors were used. Systems A and B used 20-channel receive head coils. System C used a 32 channel transmit/receive head-coil. Systems A and C used b ≈ 100, 700, 1400, and 2000 s/mm2; system B used b ≈ 100, 500, 1000, 1500, and 2000 s/mm2.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3503