3501
Differentiating Contributions To Diffusional Kurtosis in the Brain with Symmetrized Double-PFG MRI1Independent, Boston, MA, United States, 2Athinoula A. Martios Center for Biomedical Imaging, MGH and Harvard Medical School, Charlestown, MA, United States, 3Department of Radiology, University of Illinois at Chicago
Synopsis
Kurtosis imaging enables valuable diagnostics of stroke and other tissue pathologies. It can arise directly from restricted diffusion, but also from sub-voxel heterogeneity in the ADC. Utilizing double diffusion contrast, we are able to remove these heterogeneity contributions. We show this targeted ‘microscopic’ kurtosis contrast yields unique contrast in-vivo in a live rat brain: highlighting white/gray matter boundaries.
Purpose
To evaluate the contrast provided by sd-PFG double diffusion encoding by isolating contributions to diffusional kurtosis in-vivo.Method
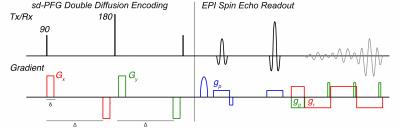
We hypothesize that the contributions to diffusional kurtosis, from diffusion being restricted by cell geometry (microscopic kurtosis, μK) and indirectly due to intra-voxel heterogeneity, occurs to varying degrees in tissue and that the isolation of μK should provide unique contrast vs. traditional kurtosis imaging (DKI).1 For μK imaging, we incorporate sd-PFG double diffusion encoding into a clinically compatable multi-slice EPI sequence (figure 1) on a 4.7T Bruker scanner (Bruker Biospec, Billerica, MA).
The sd-PFG sequence consists of a double diffusion encoding2 but utilizes a unique sampling scheme.3 It maintains the orientations of the first and second diffusion units fixed and orthogonal to each other while varying their amplitudes as $$$\cos(\phi)$$$ and $$$\sin(\phi)$$$. Direct contributions to different cumulants of the diffusion signal are isolated at distinct angular frequencies2 and are extracted by decomposing the signal $$$E(b,\phi)$$$ as
$$\ln\left\{\frac{E(b,\phi)}{E_0}\right\}=E_{c,\widetilde{0}}(b)+E_{c,\widetilde{1}}(b)\cos(\phi)+E_{c,\widetilde{2}}(b)\cos\left(2\phi\right)+ \cdot\cdot\cdot++E_{s,\widetilde{1}}(b)\sin(\phi)+\cdot\cdot\cdot$$
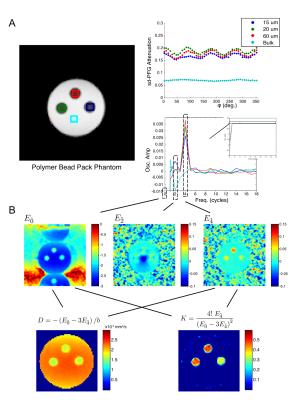
We obtain $$$E_{c/s,\omega}$$$ by computing the Fourier transform of the logarithm of each voxel normalized to unit intensity at zero encoding strength (b-value=0), masking empty regions. Kurtosis describes the 4th cumulant of the signal and is normalized by the diffusion coefficient. These quantities are isolated respectively at 4- and 0-cycles and μK is extracted by fitting
$$E_{c,\widetilde{4}}(b) = \frac{1}{4!}\left( E_{c,\widetilde{0}}(b) - 3 E_{c,\widetilde{4}}(b) \right)^2 K.$$
The distinct four cycle oscillation arising from Kurtosis can also be directly observed as a qualitative indicator of μK and a sd-PFG image is acquired with dense $$$\phi$$$ sampling to illustrate. (b-value=1500s/mm2, $$$\phi$$$ = {[0, 360), 47steps}, $$$\Delta$$$=25ms, fov = 52×52mm, matrix = 96×96) as shown for a phantom consisting of 3 water saturated polymer bead packs with bead diameters 10, 20 and 60μm (figure 2) in a water filled Epindorf tube.
To evaluate Kurtosis contrast in the brain, normal adult male Wistar rats were anesthetized throughout the MRI experiments with 1.5-2.0% isoflurane. DKI, Diffusion-weighted MRI, was acquired with spin echo (SE) EPI with 10 b-values (0, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 and 2500s/mm2), gradient pulse duration/diffusion time (δ/Δ) = 6/20 ms, TR/TE = 2500/60 ms, number of average (NAE)= 4 along six directions, and sd-PFG images (b-values=50, 250, 1000, 2500s/mm2, $$$\phi$$$= {[0, 360), 26steps}, $$$\Delta$$$=25ms, fov = 52×52mm, matrix = 96×96) are acquired.
Results
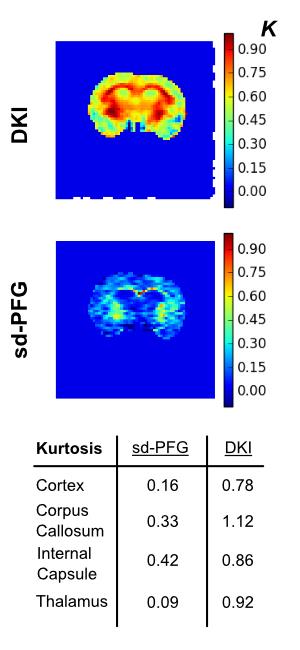
Within the brain (figure 3), the μK maps are consistently lower than conventional kurtosis maps in accordance with the fact that these maps are insensitive to heterogeneity contributions detected in DKI. The contrast provided by sd-PFG and DKI are qualitatively different: the DKI kurtosis maps have complex gradations across the brain whereas μK maps are uniform across gray matter regions with a sharp enhancement in white matter regions.Discussion
We have demonstrated that μK imaging yields a unique form of structural contrast in the brain. The study also hints that the micro-structural contribution to the kurtosis observed in DKI maps are dominated by sub-voxel ADC heterogeneity given its lower values and relative uniformity to the variations observed in DKI. Its enhancement in only white matter regions may also indicate that elevated μK should values should be expected only in regions where water is highly restricted such as in fiber bundles (e.g. structures on the order of the characteristic diffusion length $$$\sqrt{2 \Delta D_0} $$$.)
For this implementation of sd-PFG, differences in artifacts and SNR to DKI primarily arise from requiring twice the encoding time and additional refocusing pulses for a comparable measurement. For the in-vivo sample, the long encoding time strongly impacted the reconstruction quality given its T2 (~60ms) and the encoding time (~$$$2\Delta$$$ = 50ms). Nonetheless, considerable improvements are still possible for in-vivo imaging. Hardware adjustments and fitting the oscillation components directly to signal instead of its logarithm should greatly improve both measurement stability and robustness of the reconstruction.
Conclusion
Sd-PFG μK imaging shows promise as a unique form of diffusion contrast, an indicator for stroke damage, and as a research tool to understand the mechanisms dominant in diffusion contrast. Refinements in the technique to improve image quality should make it practical for routine in-vivo imaging, while additional animal studies can establish its biological interpretation and efficacy as a diagnostic.Acknowledgements
No acknowledgement found.References
1. Jensen JH, Falangola MF, et. al. Preliminary observations of increased diffusional kurtosis in human brain following recent cerebral infarction. NMR Biomed. 2011; 24(5): 452–457.
2 Mitra PP. Multiple wave-vector extensions of the NMR pulsed-field- gradient spin-echo diffusion measurement. Phys. Rev. B 1995; 51: 15074–15078.
3 Paulsen JP, Özarslan E, Komlosh ME, Basser PJ, Song YQ. Detecting compartmental non-Gaussian diffusion with symmetrized double-PFG MRI. NMR Biomed. 2015; 28(11): 1550-1556
Figures