3498
Comprehensive Correction of Motion and Nyquist Ghost Artifacts for Multi-shot Diffusion Imaging1Department of Radiology, University of Iowa, Iowa City, IA, United States, 2Department of Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States, 3GE Healthcare
Synopsis
Echo planar imaging data are often corrupted by Nyquist ghost artifacts resulting from the eddy current induced shifts between the odd & even phase encodes. Current EPI methods often rely on calibration scans that are collected prior to the data acquisition to correct for Nyquist ghosts. Unfortunately, this approach is often insufficient for the recovery of diffusion-weighted (DW) data, since the ghosting artifacts also depend on the segmentation of the EPI read-outs and diffusion weighting. We introduce a comprehensive algorithm to simultaneously correct for the eddy-current errors as well as the motion-induced artifacts in DW images that does not require any calibration scans.
Introduction
Echo planar imaging (EPI) data are often corrupted by Nyquist ghost artifacts resulting from the eddy current induced shifts between the odd & even phase encodes. Current EPI methods often rely on calibration scans that are collected prior to the data acquisition to correct for Nyquist ghosts1. Unfortunately, this approach is often insufficient for the recovery of diffusion-weighted (DW) data, since the ghosting artifacts also depend on the segmentation of the EPI read-outs and diffusion weighting. Specifically, inter-shot motion during diffusion encoding gradient can introduce additional phase variations2. The correction of both of these sources of artifacts at the same time is challenging. We introduce a comprehensive algorithm to simultaneously correct for the eddy-current errors as well as the motion-induced artifacts in DW images. The main highlight of the proposed scheme is that it does not require any calibration scans.Methods
The key idea is that image domain phase distortions, which arise from motion and eddy current induced shifts, can be modeled as the convolution between the k-space data and a small filter3. In particular, if two images differ only by a smoothly varying phase, we can find a small $$$\textit{"annihilation"}$$$ filter that captures the phase errors between the two. Using this property, we reformulate the recovery of the motion compensated multi-shot EPI dataset as the recovery of $$$2N$$$ images ($$$N$$$ is the number of shots) that satisfy Fourier domain $$$\textit{"annihilation"}$$$ relations; the $$$2N$$$ images correspond to the odd and even lines of the $$$N$$$ shots. We express the above annihilation relations compactly as a structured low-rank prior on a concatenated block-Hankel matrix (denoted by $$$\mathbf H_1$$$ illustrated in Figure 1a), which is derived from the k-space data of the components (odd/even lines of each shot). Note that each of the images are heavily under-sampled. We fill in the missing entries using a structured low-rank matrix completion algorithm, which we term as MUSSELS3.
The proposed formulation also allows us to use additional smoothness regularization into the framework to further constrain the reconstruction:\begin{equation}\label{with_TV}\hat{\tilde {\bf m}}= \text{argmin}_{{\bf \hat{m}}} {||\bf{{\cal{A}}(\hat{ m})-\hat y}}||^2_{\ell_2} + \lambda||{\bf{\bf{H_2}}}(\hat{ m})||_*,\end{equation}where $$${\bf{H_2}}$$$ is the block-Hankel structured matrix derived from the x- and y- derivatives of the k-space shot images. Note that both the priors (annihilation relations and smoothness) are compactly combined into a single regularization prior4. Here, $$$\bf{\widehat y}$$$ is the measured multi-channel multi-shot k-space data. The first term imposes data consistency to the measured k-space data using a regular SENSE formulation. The operator $$$\bf{{\cal{A}}}$$$ represents the concatenation of the following operations: $$$\bf{{\cal{M}}}\circ\bf{{\cal{F}}}\circ\bf{{\cal{S}}}\circ\bf{{\cal{F}}^{-1}}$$$ where $$$\bf{{\cal{F}}}$$$ and $$$\bf{{\cal{F}}^{-1}}$$$ represent the Fourier and the inverse Fourier transform operations respectively, $$$\bf{{\cal{S}}}$$$ represents coil sensitivities, and $$$\bf{{\cal{M}}}$$$ represents the k-space sampling mask corresponding to each shot. $$$ \lambda$$$ is a regularization parameter. The rank minimization is achieved using by minimizing the nuclear norm of the matrix $$${\bf{\bf{H_2}}}$$$ using singular value thresholding.
Data for testing the proposed method were collected on a GE MR950 7T scanner at the University of Iowa using a 2/32-channel Tx/Rx head coil in Tx mode. The imaging parameters were: FOV=25.6cm x 25.6cm; matrix size= 128 x 128 with partial Fourier acquisition. Diffusion imaging used a 4-shot Stajeskal-Tanner EPI diffusion sequence with b-value=1000s/mm2, 15 diffusion directions and one non-diffusion weighted acquisition.
Results
To compare the performance of the proposed method, a standard Nyquist ghost correction using a calibration scan was also performed on the data. Note that the calibration-based correction can only achieve 1D correction, wheres the proposed method can achieve 2D phase correction. Figure 2 shows the performance of two correction methods. The standard pipeline for the multi-shot acquisition involves Nyquist ghost correction using the calibration scan data followed by post acquisition phase calibration to correct for motion artifacts. The proposed method performs both correction in a single reconstruction, without the need for any calibration scan or explicit phase estimation. As evident from figure 2, the proposed method can correct for both the artifacts adequately whereas residual artifacts are still visible in the standard pipeline for correcting these artifacts.Conclusion
We introduced a comprehensive artifact correction scheme for multi-shot EPI diffusion data, which compensates for phase errors resulting from motion and eddy current effect. The key highlight of our method is that it does not need any calibration information, in addition to being fast. This method can also be extended to recover artifact free DWIs from partial Fourier encoded k-space data.Acknowledgements
No acknowledgement found.References
1. Xiaoping Hu and Tuong Huu Le, Artifact reduction in EPI with phase-encoded reference scan, Magnetic Resonance in Medicine, vol. 36, no. 1, pp. 166–171, jul 1996.
2. Adam W Anderson and John C Gore, Analysis and correction of motion artifacts in diffusion weighted imaging., Magnetic Resonance in Medicine, vol. 32, no. 3, pp. 379–87, 1994.
3. Mani, M., Jacob, M., Kelley, D. and Magnotta, V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magnetic Resonance in Medicine, doi: 10.1002/mrm.26382, 2016
4. K. H. Jin, D. Lee and J. C. Ye, A General Framework for Compressed Sensing and Parallel MRI Using Annihilating Filter Based Low-Rank Hankel Matrix, IEEE Transactions on Computational Imaging, vol. 2, no. 4, pp. 480-495, Dec. 2016. doi: 10.1109/TCI.2016.2601296\\
Figures

Figure 1: (a) $$${\bf{\bf{H_1}}}$$$ : Block-Hankel matrix formed using the k-space data of the components: the odd lines (magenta) and the even lines (green) of each shot). $$$\hat{\bf m}$$$ is the combined k-space data from the multi-shot EPI acquisition.
(b) $$${\bf{\bf{H_2}}}$$$ : Block-Hankel matrix for the combined Nyquist ghost artifact and motion correction with smoothness regularization. Here, the k-space data is first multiplied by $$$-j2\pi k_x$$$ and $$$-j2\pi k_y$$$ before constructing the Hankel matrix (to incorporate smoothness regularization into the reconstruction). Rank minimization of $$${\bf{\bf{H_2}}}$$$ can achieve comprehensive correction of both artifacts.
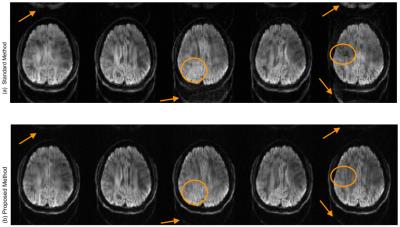
Figure 2: (a) DWIs reconstructed using a standard pipeline, where the data is first ghost corrected using calibration scan data and then motion estimated in a post acquisition calibration. This phase is then compensated in a second round of reconstruction. Incomplete artifact suppression is visible in the images as pointed out by the arrows.
(b)DWIs reconstructed using the block-Hankel matrix $$${\bf{\bf{H_2}}}$$$ by splitting odd/even lines. Both artifacts are corrected using the proposed method simultaneously. No calibration data is used.