Synopsis

Tractograms have large number of false positives. One possible solution is to use anatomically relevant atlases of bundles to create priors of known bundles and therefore concentrate on the true positives. However this requires registration with incomplete atlases that contain only a few known bundles. A new asymmetric cost function extensively advances the direct registration of tractograms to atlases with a small number of bundles. Furthermore, although existing ROI filtered atlases can miss important parts of bundles, by using a pruning method using streamline centroids, these parts can be found, and the false positives can be extensively reduced.

Introduction

Methods

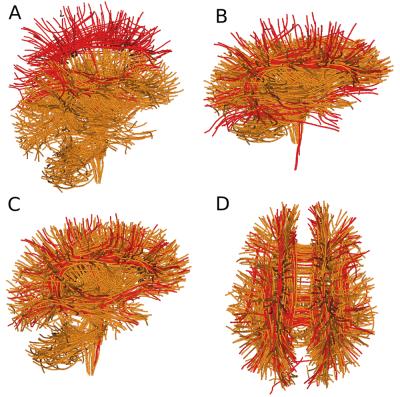
20 deterministic tractograms from 20 subjects using fields of FODs ¹² using multiple seeding and default tracking parameters. The atlases (collections of bundles per each tractogram) was generated using WMQL¹³ and further improved manually by expert neuroanatomists. See complete data description in ^{2, 3}. In order to detect and extract bundles an initial registration of a template of bundles is required and also a second step of pruning the bundles using the given templates is expected ^{5, 6}. Traditionally, researchers use the affine matrix from an image-based registration to register a target tractogram to a template however with the invention of the SLR ^{3, 4} many more possibilities are now available. In ³ it was shown that an efficient algorithm exists that can full tractograms. In this work we pushed the limits of SLR by asking the algorithm to register the target’s tractograms with a streamline atlas containing only a few bundles. This is a truly hard registration problem because there are very few similarities between the atlas (red) and the initial tractogram (orange) (see Fig. 1A). To do the registration we initially used the symmetric cost function shown in ³ known as the BMD ³. This is known to be robust with incomplete datasets. However, this cost function was not able to register properly the centroids as shown in Fig. 1B because the differences between the atlas (red) and the target (orange) were severely large. For example, notice that the atlas had no bundles near the cerebellum. The solution was to create an asymmetric version of the BMD where we weighted only the closest streamlines from the target to the atlas and not from the atlas to the streamlines. Afterwards, distance matrices between the atlas bundles centroids and another full brain tractogram were created to detect relevant close bundles (as shown in ^{5, 6}) from the atlas. The centroids were generated using QuickBundles ⁴ with a distance threshold of 15mm and resampling at 20 points per streamline. The pruning thresholds used were 10-15mm.

Results

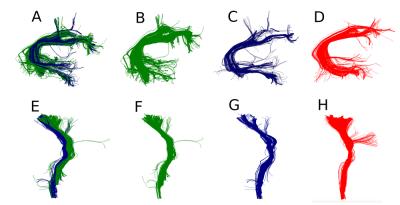
We can see the extensive improvement of registration using an asymmetric cost function in Fig. 1C and D. This is an outstanding result as the atlas (red) had only 150 centroids summarizing 27 bundles and the target has 740 centroids summarizing hundreds of bundles. Now that we have the atlas and the target in the same space we can run different algorithms that can detect atlas bundles in the target’s tractogram. These can then be used to do tractometry ^{7, 9, 10, 11}. In the following experiment, we studied the quality of atlases generated from different tractograms. The goal here was to show that after registration we can detect similar bundles and examine how good were those bundles in comparison to the expert bundles. For this purpose we took pairs of subjects. Removed a specific expert bundle from the second subject, then used the corresponding expert bundle from the first subject and performed streamline-based pruning using QuickBundles ⁴ centroids and a distance matrix between the centroids bundles and the hole streamlines of the other tractograms (with the specific bundle removed). Surprisingly, we observed that not only we can detect the bundles but we can find streamlines that should have been a part of the expert bundle. (see Fig. 2).

The segmented bundles from the experts had missing parts which were not detected by the expert but they do exist in the tractograms. This is clearly a problem related to the use of ROIs for filtering. This observation was the same across different manual or automated atlases and across different tractograms. For example, similar issues were found during the ISMRM 2015 tractography challenge ¹ and alleviated using streamline distances ³.

Conclusion

Acknowledgements

References

[1] Maier-Hein K., Neher P., Houde J.C., Cote M-A, Garyfallidis E., Descoteaux M., et. al Tractography-based connectomes are dominated by false-positive connections, Biorxiv (2016).

[2] Renauld E, Descoteaux M, Bernier M, Garyfallidis E, Whittingstall K. Semi-Automatic Segmentation of Optic Radiations and LGN, and Their Relationship to EEG Alpha Waves. PloS one. 2016 Jul 6;11(7):e0156436.

[3] Garyfallidis, E., Ocegueda, O., Wassermann, D., Descoteaux, M. Robust and efficient linear registration of white-matter fascicles in the space of streamlines. NeuroImage 2015 117, 124–140.

[4] Garyfallidis, E., Brett, M., Correia, M.M., Williams, G.B., Nimmo-Smith, I., QuickBundles, a method for tractography simplification. Frontiers in neuroscience (2012) 6, 1–13.

[5] Labra, N., Guevara, P., Duclap, D., Houenou, J., Poupon, C., Mangin, J.F., Figueroa, M. Fast automatic segmentation of white matter streamlines based on a multi-subject bundle atlas. Neuroinformatics (2016), 1–16.

[6] Yoo, S.W., Guevara, P., Jeong, Y., Yoo, K., Shin, J.S., Mangin, J.F., Seong, J.K. An example-based multi-atlas approach to automatic labeling of white matter tracts. PloS ONE (2015) 10, e0133337.

[7] Dayan M., Monohan E., Pandya S., Kuceyeski A., Nguyen TD, Raj A, Gauthier SA. Profilometry: A new statistical framework for the characterization of white matter pathways, with application to multiple sclerosis. Human brain mapping. (2016) Mar 1;37(3):989-1004.

[8] O’Donnell, L.J., Westin, C.F. Automatic tractography segmentation using a high-dimensional white matter atlas. Medical Imaging, IEEE Transactions on (2007) 26, 1562–1575.

[9] O’Donnell, L.J., Westin, C.F., Golby, A.J. Tract-based morphometry for white matter group analysis (2009). NeuroImage 45, 832–844.

[10] Yeatman, J.D., Dougherty, R.F., Myall, N.J., Wandell, B.A., Feldman, H.M. Tract profiles of white matter properties: Automating fiber-tract quantification. PLoS ONE 7 (2012), e49790.

[11] Bells S, Cercignani M, Deoni S, Assaf Y, Pasternak O, Evans CJ, Leemans A, Jones DK. Tractometry–comprehensive multi-modal quantitative assessment of white matter along specific tracts. InProc. ISMRM 2011 (Vol. 678).

[12] Tournier J, Calamante F, Connelly A. MRtrix: diffusion tractography in crossing fiber regions. International Journal of Imaging Systems and Technology. (2012) Mar 1;22(1):53-66.

[13] Wassermann D, Makris N, Rathi Y, Shenton M, Kikinis R, Kubicki M, Westin CF. The white matter query language: a novel approach for describing human white matter anatomy. Brain Structure and Function. 2016 Jan 11:1-7.