3489
Effect of Different Seeding Strategies on Tractometry Reproducibility1Sherbrooke Connectivity Imaging Laboratory (SCIL), Université de Sherbrooke, Sherbrooke, QC, Canada, 2Center for Information and Neural Networks (CiNet), National Institute of Information and Communications Technology (NICT), Suita, Japan, 3Graduate School of Frontier Biosciences, Osaka University, Suita, Japan
Synopsis
Two common approaches to tractography seeding are using the whole-brain white matter mask, or the gray and white matter interface. Using a dataset with two acquisitions per subject and a state of the art processing pipeline, we compared the test-retest reproducibility of the shape and tract profiles of major white matter bundles for both seeding strategies. We found that both seeding strategies have regions in the brain where they are more reproducible. We propose an ensemble method combining both strategies as a possible way to make tractometry from white matter bundles more robust.
Introduction
Tractography uses diffusion MRI to estimate the position, trajectory and structural property of major white matter tracts by tracking the orientation of the local diffusion signal1,2. Tractography algorithms require a seeding mask region from which initial voxels are sampled to generate a streamline. There are two popular proposed strategies on sampling seed voxels. The first strategy is to ramdomly select any voxel from the whole white matter volume, and repeat this process until a whole-brain tractogram of the desired size is obtained3,4. The second strategy is to select voxels specifically located at the intersection of the gray and white matter, also called gray matter一white matter interface (GMWMI) seeding5,6,7. Figure 1 illustrates the seeding masks typically used for each strategy. These two fundamentally different strategies generate quite distinct candidate tractograms5. In this study, we evaluate the test-retest reproducibility of these methods at the white matter bundle level in terms of their shape and volume, and tractometry values. Finally, we propose a method to combine streamlines derived from different seeding strategies in order to integrate the advantages of each strategy8.Methods
Diffusion-weighted MRI images were acquired from five healthy male subjects at Stanford University (STN96 dataset8,9,10), aged from 27 to 40 years old. A dual spin echo diffusion-weighted sequence was used with 96 different directions at a spatial resolution of 1.5 mm3 isotropic using a b-value of 2000 s/mm2. Ten non-diffusion weighted (b = 0) images were acquired at the beginning of each scan, and each subject was scanned twice.
Whole-brain probabilistic tractography was performed using the tckgen command of the MRtrix3 diffusion tools11,12. For the scope of this study, default parameters were kept constant (step size of 0.75 mm, maximum angle of 45° per step, maximum length of 150 mm, etc.). For the gray matter一white matter interface seeding, the MRtrix3 framework of Anatomically-Constrained Tractography (ACT) was used6. For both seeding strategies, streamlines were generated until 10 million streamlines obeyed MRtrix’s streamline acceptance criteria. Experiments were conducted for different numbers of streamlines and similar trends were observed, but only results from 10 million streamlines are reported in this abstract.
An ensemble method that combines streamlines from both seeding strategies was also tested. Simply put, half of the streamlines are randomly sampled from each tractogram, and combined into a resulting ensemble tractogram8. Then, major white matter bundles were extracted from each tractogram using the White Matter Query Language (WMQL)13. Each bundle was then processed using SCIL’s tractometry pipeline14, similar to Automated Fiber Quantification (AFQ)15, in order to extract tract profiles of fractional anisotropy (FA) values along each bundle.
Reproducibility of bundles were evaluated in two ways: first, in terms of the overlap of the volume of the bundles. Bundles of same subject acquisitions were linearly registered to each other, and a Dice coefficient overlap measure was computed16. Then, the reproducibility of the tractometry was evaluated. A Euclidean distance was computed between same subject FA tract profiles of each bundle. Both seeding strategies and the ensemble method were then compared for each bundle and evaluation method.
Results
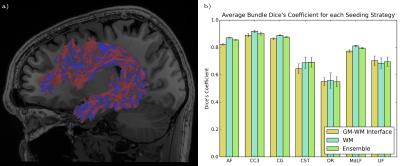
Figure 2 illustrates the differences of each strategy in Dice’s coefficient for selected bundles. We observed that WM seeding produces higher reproducibility in shape and volume as compared with GMWMI seeding strategy. This may be due to the nature of GMWMI seeding: it produces streamlines that reach the gray matter, which increases the fanning and therefore variability of bundles due to the probabilistic nature of tractography.
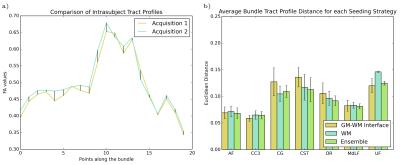
Figure 3 illustrates the FA tract profile distances of selected bundles for each strategy. We see a trend where GMWMI seeding is more reproducible in commissural and smaller bundles (e.g. CC, UF). Conversely, WM seeding is more reproducible in bigger, straighter bundles (e.g. CG, CST). Also, we see that the ensemble method can provide a compromise between the two strategies, and can sometimes even be more reproducible than either of them (e.g. CST, OR).
Conclusion
We have shown that tractometry can provide a helpful way to validate the reproducibility of tractography results. Both studied seeding strategies seem to have their own benefits and drawbacks. GMWMI seeding produces more fanning bundles and is more reproducible in commissural and smaller bundles while WM seeding is more reproducible in bigger, straighter bundles. Finally, the proposed ensemble method is a promising way to get a good compromise between both strategies. As only major WM bundles were studied, we encourage further studies focusing on specific bundles to do a similar analysis in order to choose which seeding strategy to use.Acknowledgements
We are grateful to the National Institute of Communications Technology (NICT) of Japan and to the Japan Society for the Promotion of Science (JSPS) for funding this project. We would also like to thank Kaoru Amano and Noboru Nushi for providing the computer environment, Jean-Christophe Houde for his help with the processing pipeline, and Ariel Rokem and Jason D. Yeatman for acquiring the data.References
1. Basser, P. J., Pajevic, S., Pierpaoli, C., Duda, J., and Aldroubi, A. "In vivo fiber tractography using DT-MRI data." Magnetic Resonance in Medicine, vol. 44, no. 4 (2000): 625-632.
2. Jbabdi, S., and Heidi, J. B. "Tractography: where do we go from here?." Brain Connectivity, vol. 1, no. 3 (2011): 169-183.
3. Conturo, T. E., Lori, N. F., Cull, T. S., Akbudak, E., Snyder, A. Z., Shimony, J. S., Raichle, M. E., et al. "Tracking neuronal fiber pathways in the living human brain." In proc. of the National Academy of Sciences, vol. 96, no. 18 (1999): 10422-10427.
4. Tournier, J. D., Mori, S., and Leemans, A. "Diffusion tensor imaging and beyond." Magnetic Resonance in Medicine, vol. 65, no. 6 (2011): 1532-1556.
5. Li, L., Rilling, J. K., Preuss, T. M., Glasser, M. F., and Hu, X. "The effects of connection reconstruction method on the interregional connectivity of brain networks via diffusion tractography." Human Brain Mapping, vol. 33, no. 8 (2012): 1894-1913.
6. Smith, R. E., Tournier, J. D., Calamante, F., and Connelly, A. "Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information." NeuroImage, vol. 62, no. 3 (2012): 1924-1938.
7. Girard, G., Whittingstall, K., Deriche, R., and Descoteaux, M. "Towards quantitative connectivity analysis: reducing tractography biases." NeuroImage, vol. 98 (2014): 266-278.
8. Takemura, H., Caiafa, C. F., Wandell, B. A., and Pestilli, F. "Ensemble Tractography." PLoS Comput Biol, vol. 12, no. 2 (2016): e1004692.
9. Rokem, A., Yeatman, J. D., Pestilli, F., Kay, K. N., Mezer, A., van der Walt, S., & Wandell, B. A. "Evaluating the accuracy of diffusion MRI models in white matter." PloS ONE, vol. 10, no. 4 (2015): e0123272.
10. Pestilli, F., Yeatman, J. D., Rokem, A., Kay, K. N., and Wandell, B. A. "Evaluation and statistical inference for human connectomes." Nature Methods, vol. 11, no. 10 (2014): 1058-1063.
11. Tournier, J., Calamante, F., and Connelly, A. "MRtrix: diffusion tractography in crossing fiber regions." International Journal of Imaging Systems and Technology, vol. 22, no. 1 (2012): 53-66.
12. Calamante, F. and Connelly, A. "Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions." In proc. of ISMRM, vol. 18 (2010): 1670.
13. Wassermann, D., Makris, N., Rathi, Y., Shenton, M., Kikinis, R., Kubicki, M., and Westin, C. F. "On describing human white matter anatomy: the white matter query language." In proc. of MICCAI, vol. 8149 (2013): 647-654.
14. Cousineau, M., Garyfallidis, E., Côté, M. A., Jodoin, P. M., and Descoteaux, M. "Tract-profiling and bundle statistics: a test-retest validation study." In proc. of ISMRM, vol. 24 (2016): 3436.
15. Yeatman, J. D., Dougherty, R. F., Myall, N. J., Wandell, B. A., and Feldman, H. M. "Tract profiles of white matter properties: automating fiber-tract quantification." PLoS One, vol. 7, no. 11 (2012): e49790.
16. Dice, L. R. "Measures of the amount of ecologic association between species." Ecology, vol. 26, no. 3 (1945): 297-302.
Figures