3485
High-Throughput Diffusion Imaging Using Multiple Coils for Mouse Brain Connectomics1Center for In Vivo Microscopy, Duke University Medical Center, Durham, NC, United States, 2Radiology, Duke University Medical Center, Durham, NC, United States
Synopsis
The complex neural architecture and brain connectivity of mouse models of human disease can be studied ex vivo by diffusion tensor imaging; however, acquisition times are long and make cohort studies prohibitively time-consuming. Throughput can be increased by the simultaneous use of multiple coils placed in proximity to the magnet isocenter. We quantify the impact of the multiple-coil configuration on throughput, on diffusion metrics used in tractography, and on mouse brain connectivity matrices. We show that fractional anisotropy is underestimated off-isocenter, while the main eigenvector direction is minimally affected. The effect on brain connectivity networks is currently being quantified.
Purpose
Alterations in brain connectivity may be correlated with neurologic disease, spurring an interest in brain connectivity mapping of mouse models of human disease. Complex neural architecture can be delineated by diffusion tensor imaging1-6; however, acquisition times of a mouse brain specimen are typically long, ranging from a dozen hours7 to several days8. As a result, cohort studies9 can become prohibitively time-consuming.
Throughput can be increased by the simultaneous use of multiple coils10,11, shielded from each other and each at a distance from magnet isocenter. However, shielding can degrade SNR and throughput. Moreover, off-isocenter imaging may bias DTI metrics due to gradient inhomogeneity12. In this abstract, we quantify the impact of the multiple-coil configuration on SNR, on diffusion imaging metrics used in tractography, and on mouse brain connectivity maps.
Method
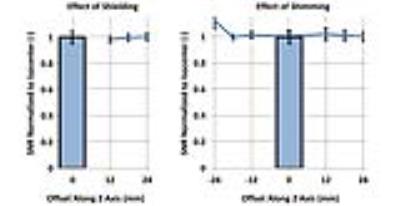
For our 7T horizontal bore magnet (Bruker BioSpec 70/20, Billerica, MA), equipped with a 114mm inner-diameter gradient set (model BGA-12S2) capable of 440 mT/m, we developed a two-coil system where the position of each coil within its shield, and consequently the coil offset to magnet isocenter, can be adjusted. Three offsets were studied: 12mm, 18mm, and 24mm, in each direction along the magnet axis. At each coil location, we measured the SNR change (TR/TE/FOV/BW/voxel: 200ms/5.4ms/25.6x12.8x12.8mm/100kHz/200um) due to alterations in shield proximity and in shimming volume, using a homogeneous phantom (Figure-1).
At the different coil positions, the same mouse brain specimen was scanned, using a uniformly-distributed, rotationally-invariant13 21-direction 3D spin-echo diffusion sequence at a b-value of 1500s/mm2 (TR/TE/FOV/BW/voxel: 100ms/20ms/25.6x12.8x12.8mm/100kHz/100um). Each dataset was rigidly registered to a common atlas (Waxholm Space14). Then the diffusion directions were rotated accordingly, and finally the diffusion metrics were computed. That way, registration does not include inaccuracies stemming from eigenvector interpolation.
To provide a ground truth for comparison, data was also acquired from a single, unshielded coil on magnet isocenter.
At each coil position, the fractional anisotropy (FA) was calculated. To quantify the change in orientation of the main eigenvectors, the dot product between the on-isocenter eigenvector dataset and each off-isocenter dataset was calculated, expressed as an angular deviation.
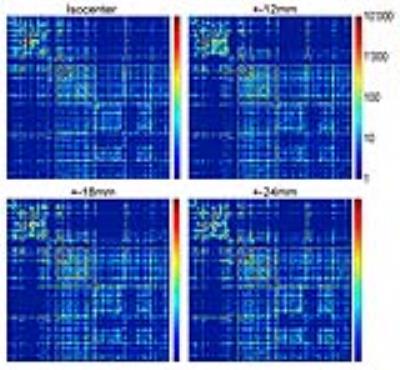
Subsequently, at each coil location, we computed tractography maps using deterministic fiber tracking15. Finally, from the brain regions identified in Waxholm Space, a connectivity matrix was calculated (Figure-2).
Results
At the 6 tested offsets, SNR deterioration due to shielding or shimming was minimal (Figure-3).
In contrast, fractional anisotropy, averaged within different brain regions, was underestimated away from isocenter. The underestimation increases with distance from isocenter, up to -30% (Figure-4). The measurement is noisier in low-FA brain region than in high-FA region.
The main eigenvector in each voxel of the sets acquired off-isocenter, compared to the same voxel of the set on isocenter, suffers from a greater deviation when the mouse brain acquisition takes place further away from isocenter. But, the deviation amounts to a few degrees only.
Qualitatively, the connectivity matrices corresponding to each coil offset look similar (Figure-5). Regions highly connected with each other appear consistently regardless of the position of the coil. However, off-isocenter imaging may degrade the strength of the connection between regions showing a lesser connectivity with each other.
Discussion
When the coils are 12mm away from isocenter, a SNR penalty of 3% (within the error bar) corresponds to a throughput gain of 1.9, not significantly different from the maximum throughput gain of 2.
When operating the coils 12mm away from isocenter, FA underestimation due to off-isocenter imaging (10-15%) is compounded to the change due to specimen aging and fixation. Normalization can help compare specimens acquired by a multiple-coil system to a single coil.
The measurement error of the eigenvector direction, in general, is small. It alters fiber track trajectories, causes false positive connections between regions, and reduces true connectivity. Qualitatively, the effect on the connectivity matrix appears small.
Imperfect registration has an effect –which has not been assessed– of the entire analysis, relying on a voxel-to-voxel comparison within brain regions. Also, the voxel size is coarse (100um) and may mask subtle effects.
Conclusion
The throughput of diffusion tensor imaging of mouse brain specimens can be increased by a factor of 1.9, when the two coils are 12mm away from isocenter. Off-isocenter imaging significantly underestimates FA (10-15%); however, errors in the primary eigenvector direction are small (3-4°). As a result, the connectivity matrices seem minimally affected by the two coil configuration. Quantitative assessment of the network differences is under way.Acknowledgements
Support provided by the Duke Center for In Vivo Microscopy, an NIH Biomedical Technology Resource Center (P41 EB015897).References
1. Basser, P. J., Mattiello, J. & Lebihan, D. MR diffusion tensor spectroscopy and imaging. Biophysical Journal 66, 259–267 (1994).
2. Le Bihan, D. Looking into the functional architecture of the brain with diffusion MRI. Nature Reviews Neuroscience 4, 469–480 (2003).
3. Mori, S. & Zhang, J. Principles of diffusion tensor imaging and its applications to basic neuroscience research. Neuron 51, 527–539 (2006).
4. Wedeen, V. J. et al. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. NeuroImage 41, 1267–1277 (2008).
5. Tournier, J. D., Calamante, F., Gadian, D. G. & Connelly, A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. NeuroImage 23, 1176–1185 (2004).
6. Tuch, D. S. Q-ball imaging. Magnetic Resonance in Medicine 52, 1358–1372 (2004).
7. Ruest, T. et al. High-resolution diffusion tensor imaging of fixed brain in a mouse model of Pelizaeus-Merzbacher disease: comparison with quantitative measures of white matter pathology. NMR in Biomedicine 24, 1369–1379 (2011).
8. Calabrese, E., Badea, A., Cofer, G., Qi, Y. & Johnson, G. A. A Diffusion MRI tractography connectome of the mouse brain and comparison with neuronal tracer data. Cereb. Cortex 25, 4628–4637 (2015).
9. Zhang, J., Jones, M. V., McMahon, M. T., Mori, S. & Calabresi, P. A. In vivo and ex vivo diffusion tensor imaging of cuprizone-induced demyelination in the mouse corpus callosum. Magnetic Resonance in Medicine 67, 750–759 (2012).
10. Bock, N. A., Nieman, B. J., Bishop, J. B. & Henkelman, R. M. In vivo multiple-mouse MRI at 7 Tesla. Magnetic Resonance in Medicine 54, 1311–1316 (2005).
11. Zhang, X., Schneider, J. E., Portnoy, S., Bhattacharya, S. & Henkelman, R. M. Comparative SNR for high-throughput mouse embryo MR microscopy. Magnetic Resonance in Medicine 63, 1703–1707 (2010).
12. Bammer, R. et al. Analysis and generalized correction of the effect of spatial gradient field distortions in diffusion-weighted imaging. Magnetic Resonance in Medicine 50, 560–569 (2003).
13. Skare, S., Hedehus, M., Moseley, M. E. & Li, T. Q. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. Journal of Magnetic Resonance 147, 340–352 (2000).
14. Johnson, G. A. et al. Waxholm Space: An image-based reference for coordinating mouse brain research. NeuroImage 53, 365–372 (2010).
15. Yeh, F.-C., Verstynen, T. D., Wang, Y., Fernandez-Miranda, J. C. & Tseng, W.-Y. I. Deterministic diffusion fiber tracking improved by quantitative anisotropy. PLOS ONE 8, e80713 (2013).
Figures