3466
Reduction of susceptibility-induced field gradients in multi-fibre diffusion phantoms via susceptibility matching1Institute of Neuroscience and Medicine 4, Forschungszentrum Jülich, Jülich, Germany, 2Department of Neurology, Faculty of Medicine, RWTH Aachen University, Aachen, Germany, 3JARA – BRAIN – Translational Medicine, RWTH Aachen University, Aachen, Germany
Synopsis
Studies performing diffusion-weighted MRI on anisotropic fibre phantoms suffer from microscopic background field gradients induced by differences in the magnetic susceptibility of the employed materials. We present a particularly promising approach that makes use of a matched magnesium chloride solution to eliminate these effects. The method is thoroughly studied and successfully validated on a crossing-fibre phantom containing two perpendicularly crossing fibre populations. The obtained results are no longer subject to any orientation-dependence with respect to B0.
Purpose
Anisotropic fibre phantoms are nowadays increasingly used in diffusion-weighted (DW) MRI1,2. Polyethylene fibres have excellent properties regarding the restriction of water diffusion and surface relaxation properties1,2. Yet, the magnetic susceptibility of polyethylene fibres is usually different from that of the liquid in the interstitial space. This produces strong, microscopic background field gradients when the fibres are not aligned with the static magnetic field (B0)2,3. We investigate an approach to reduce the susceptibility-induced background gradients in multi-fibre diffusion phantoms via matching the magnetic susceptibility of the liquid to that of the fibres. An aqueous solution of magnesium chloride hexahydrate (MgCl2•6H2O) is employed.Methods
The magnetic susceptibility of distilled water4 is χw ≈ -9.05ppm, whereas for Dyneema one encounters2 χd ≈ -10ppm. Most salts show susceptibility values lower than that of water. Yet, they also have high electrical conductivity5. Magnesium chloride (MgCl2) has a susceptibility of χ = -19.6ppm6. It is also highly soluble in water with up to 552g/l at 20°C6 and its conductivity at a mass percentage of 25% is only half as strong as e.g. for NaCl. The hydrated form, MgCl2•6H2O, can easily be mixed with water.
Susceptibility matching: Nine solutions were prepared with increasing MgCl2•6H2O concentration, cv (0≤cv≤3.55mol/l, v=0…8). Test vials were filled and embedded, one at a time, into a cylindrical PET plastic container oriented perpendicular to B0. Magnetic susceptibility is assessed via the field distortions generated by the test vial in the surrounding water3. All MRI experiments were carried out in a whole-body 3T Siemens MAGNETOM Trio scanner. The field distribution in the phantom is estimated using the phase of a multiple echo GRE sequence7. For unwrapping and background field correction we use in-house software (URSULA8, MUBAFIRE9).
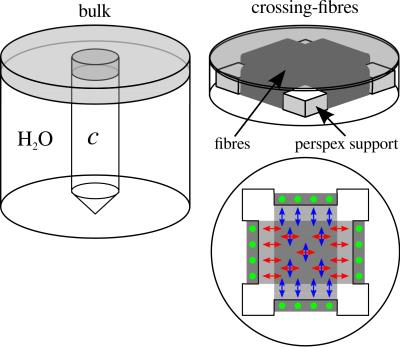
DW MRI: Bulk diffusivity is assessed for all nine concentrations using the double-refocused spin-echo EPI sequence. In order to investigate the benefits of the matching concentration, cmatched, a crossing-fibre phantom was constructed by winding Dyneema fibres around a Perspex support1 (Figure 1). DW MRI experiments were carried out for two cases:
1. Unmatched case. The phantom was filled with distilled water.
2. Matched case. The phantom was drained and refilled with cmatched.
Experiments were performed for three orientations of the phantom such that the angle θ between one of the fibre populations and B0 was θ = 0º, 22.5º, 45º. Measurement parameters included: b-values, b = 0, 1.0 ms/μm2 (unmatched case) and b = 0, 2.0 ms/μm2 (matched case) along 64 gradient directions. Thus the product bD remains comparable for both cases. Diffusion tensor imaging analysis is performed using in-house Matlab scripts. Furthermore, the performance of the constrained spherical deconvolution (CSD) and q-ball imaging (QBI) methods in assessing fibre directionality is evaluated using ExploreDTI11.
Results and discussions
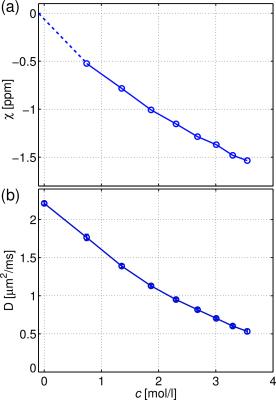
A nearly linear dependence of the magnetic susceptibility of the solutions with the molar concentration is observed (Figure 2a). The concentration at which the magnetic susceptibility matches that of the fibres is nearly c3 = 1.87mol/l. A concomitant reduction of the bulk diffusivity is observed (Figure 2b).
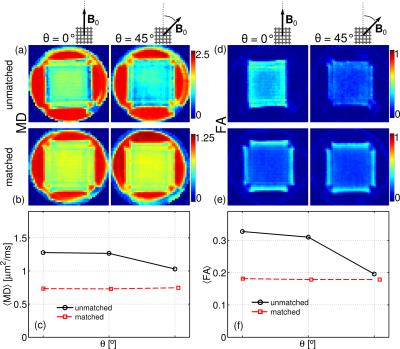
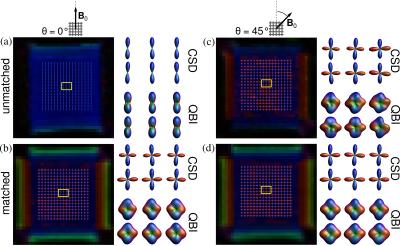
Figure 3 shows the maps of the mean diffusivity (MD) and fractional anisotropy (FA) for the unmatched and matched case and two orientations: θ = 0º, 45º. All maps exhibit orientation-dependent changes in the unmatched case, whereas in the matched case these changes virtually disappear. Figures 3c and 3f show the average values within a region-of-interest. One can observe a strong dependence of MD and FA with the orientation of the phantom for the unmatched case, whereas for the matched case they remain constant. The performance of CSD and QBI is depicted in Figure 4 for unmatched and matched case with the orientations θ = 0º, 45º. For the unmatched case and θ = 0º only the fibre population parallel to B0 is resolved (Figure 3a). For θ = 45º both fibre populations can be resolved (Figure 3c). Yet, for the matched case both fibre populations are resolved, regardless of the phantom orientation (Figures 4b and 4d).
Conclusion
We demonstrate that the effect of microscopic, susceptibility-induced field gradients on diffusion metrics in multi-fibre diffusion phantoms can be greatly reduced by matching the susceptibility of the liquid to that of the fibres with MgCl2•6H2O. We can thus design phantoms where diffusion metrics are independent of the fibre orientation with B0 which is particularly important when studying multiple-fibre populations B0.Acknowledgements
No acknowledgement found.References
1. E. Farrher et al., Magn. Reson. Imaging 30, 518-526 (2012);
2. E. Fieremans et al., Phys. Med. Biol. 53, 5405-5419 (2008);
3. J. Lindemeyer et al., Proc. Int. Soc. Mag. Reson. Med. 23, 0157 (2015);
4. J. F. Schenck. Medical Physics 23, 815–50 (1996);
5. B. Raton, CRC Handbook of Chemistry and Physics - Electrical Conductivity of Aqueous Solutions. CRC Press, 70th editi ed. (1989);
6. B. Raton. CRC Handbook of Chemistry and Physics, Internet Version 2005. CRC Press (2005);
7. P. A. Yushkevich et al. Neuroimage 31, 1116–1128 (2006); [8] J. Lindemeyer et al. Proc. Int. Soc. Mag. Reson. Med. 21, 2494 (2013);
9. J. Lindemeyer, et al., PLoS One 10e0138325 (2015);
10. Koch et al., Phys. Med. Biol., 51(24), 6381–402, (2006);
11. A. Leemans, et al., Intl. Soc. Mag. Reson. Med. 17, 3537 (2009).
Figures