3463
Histological validation of microstructural measures derived from the PICASO model1Harvard Medical School, Boston, MA, United States, 2Polytechnique Montréal
Synopsis
We propose to validate the PICASO (Precise Inference and Characterization of Structural Organization)1 biophysical model of tissue microstructure using a full-slice histology of cat spinal cord. The PICASO model was fit to high resolution diffusion MRI (dMRI) of a cat spinal cord to estimate microstructural measures of diffusion disturbance, which is directly related to axonal packing and density. We found that the structural disturbance coefficient (SDC) in the direction orthogonal to the fiber orientation from the PICASO model was strongly correlated with the axonal density obtained from histology2, with a correlation coefficient of r=0.67. Thus, the SDC could provide very precise information about the microscopic arrangement of axons or cells in biological tissue.
Purpose
The PICASO model1 was derived by solving the fundamental diffusion equation with a spatially varying diffusivity term (to account for restrictions and hindrances), which captures the microscopic organization of cells in biological tissue. In particular, it is able to disentangle the contribution of structural disturbances to molecular motion from the diffusivity of the water molecules. The structural disturbances to water diffusion provides important information about the microscopic arrangement of axons or cells in tissue structures. It was shown1 in our earlier work on in-vivo human brain data that the estimated SDC was very sensitive to axonal packing and density. In this work, we validate the PICASO model by computing the correlation between SDC and the axonal density derived from histology.Methods
Histology: Ex-vivo tissue preparation was done as described in our earlier work2. A slice of spinal cord was stained with osmium 4% dehydrated, embedded in paraffin, cut in 4 mm slices. The resolution was 230 nm/px. The axons were automatically segmented using the AxonSeg software3: https://github.com/neuropoly/axonseg. A contiguous slice was scanned using an optical 20x whole slice microscope (Hamamatsu NanoZoomer 2.0-HT) for the histology data. MRI: The MRI data was acquired from an axial slice in a cervical segment of cat spinal cord on an Agilent 7T animal scanner equipped with 600 mT/m gradients. The spatial resolution of diffusion MRI data was 0.16x0.16x0.20 mm3. The matrix size was 64x64. The diffusion parameters were d=3 ms, D=30 ms, TE=47 ms. Diffusion gradients were acquired along 796 directions in 4 shells with b-values of 40/189/1680/6720 s/mm2. PICASO model: The microstructure of the tissue is captured by a structural disturbance function u(q,t), which provides information about the spatial distribution of the disturbances, where q is in the reciprocal space of displacement. In practice, if dMRI data is measured at a single diffusion time, we can assume that u(q,t) is time-invariant. Moreover, if the data is measured at low q-value, we can use a polynomial model to approximate the disturbances. Following our earlier work1, we fitted the dMRI measurements to the following PICASO model:$$s(b,{\bf n})={\bf n}^TM{\bf n}+(1-{\bf n}^TM{\bf n})\exp(-b{\bf n}^TM{\bf n}),$$where n is the gradient direction vector with unit norm, M is a positive definite tensor with the same set of eigenvectors as D, and the D is assumed to have a cylindrical shape with two identical small eigenvalues. Assuming time-independence of the diffusion disturbance as $$$u({\bf q})={\bf n}^TM{\bf n}{\bf q}^TD{\bf q}$$$, the model parameters were estimated by solving a nonlinear least squares problem. The SDC’s were estimated as the eigenvalues of the product MD along the perpendicular direction of axons1. We note that the unit of SDC is μm2/ms, which is the same as that of diffusivity. SDC can be considered as the amount of reduced diffusivity due to structural restrictions and hindrances and hence is related to the axonal density and packing. Validation: The axon-segmented image was down-sampled to the same resolution as dMRI data and registered to MRI using affine transformation. Correlation coefficient was computed between the estimated SDC and the number of axons in each voxel.
Results
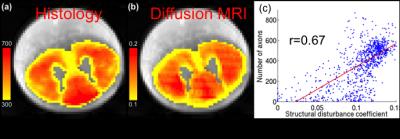
Figure 1a illustrates the estimated number of axons per voxel (axon density) from histology results. A majority of the number of axons per voxel is between 300 and 700. Figure 1b shows the map of the estimated diffusion disturbance coefficients. The two images have similar contrast. In particular, the low axonal density region has lower structural disturbance. Figure 1c demonstrates that the number of axons is strongly correlated to the SDC, with the Pearson correlation coefficient of r=0.67. Moreover, the correlation coefficient between SDC and axonal diameter and the fraction of restricted water is 0.59 and 0.60, respectively.Discussion
We note that several other quantitative MRI metrics derived from DTI, AxCaliber, ActiveAx and NODDI have been validated using the same slice of histology in2. It was shown that the estimated axon diameter using AxCaliber had high correlation coefficient (r=0.62) with that obtained from histology. However, the diffusion MRI data used for AxCaliber had multiple diffusion times with d=3/8/8/8 ms, and D=7/12/25/40 ms. But, the SDC estimated using our PICASO model only used MRI data acquired at a fixed diffusion time. We also note that the low-axonal-density region has large axonal diameters of about 4.5 mm, while the displacement of water molecules for the multi-shell data is about mm (in the best case scenario), which is not much larger than the axon diameter. Thus, in this experimental setup, the water molecules have not “explored” the microstructure comprehensively in regions with large diameters. Thus, with a longer diffusion time, we expect the PICASO model to perform even better, which we will explore in our future work.Acknowledgements
No acknowledgement found.References
1. L. Ning, et al., Precise Inference
and Characterization of Structural Organization (PICASO) of tissue from
molecular diffusion. Accepted by NeuroImage, 2016.
2. T. Duval, et al., Validation of
quantitative MRI metrics using full slice histology with automatic axon segmentation.
Singapore, ISMRM; 2016.
3. Zaimi A, Duval T, Gasecka A, Côté D, Stikov N, Cohen-Adad
J. AxonSeg: open source software for axon and myelin segmentation and
morphometric
analysis. Front Neuroinform 2016;10(37).