3460
A Novel Yeast Cells- and Microcapillaries-Based Phantom for Validation of Diffusion MRI Models1School of Chemistry, The Raymond and Baverly Sackler Faculty of Exact Science, Tel Aviv University, Tel Aviv, Israel, 2School of Mathematical Sciences, The Raymond and Beverly Sackler Faculty of Exact Science, Tel Aviv University, Tel Aviv, Israel, 3Sagol School of Neuroscience, Tel Aviv University, Tel Aviv, Israel
Synopsis
Numerous different models provide detailed microstructure information from diffusion MRI data. In order to challenge them, there is a need for complex phantoms with known structural characteristics. For this purpose, we present a novel phantom, consists of spherical fixed yeast cells and cylindrical microcapillaries. Despite of its complexity, arising from the different size, geometry and size distribution of the restricted compartments, there is a good correlation between the known ground truth and the features that were extracted from fitting single diffusion encoding (SDE) MRI experimental data, assuming continued or discrete weight of size distribution.
Introduction
Noninvasive determination of CNS microstructure, for example, is paramount1. Therefore, when new methodologies are proposed to study microstructural characteristics of complex biological tissues, it is important to estimate the accuracy and limitations of the methods. One way to address this issue is to validate these methodologies using complex albeit well-defined phantoms with known microstructural features2-5. In this work, we suggest a novel phantom characterized by two restricted compartments that differ in geometry (spheres and cylinders), size and type of weight distribution (discrete vs. continued). The smaller and isotropic spherical compartment is consisting of yeast cells, while the larger and anisotropic cylindrical compartment is composed of microcapillaries having a discrete weight distribution. To obtain the microstructural information of this complex phantom, we fitted the single diffusion encoding (SDE) MRI experimental data3, assuming continued or discrete weight distribution. Then, the extracted structural features were compared to the known characteristics of the phantom.Methods
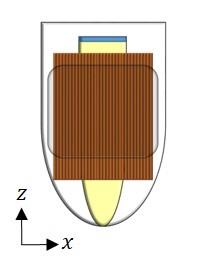
Figure 1 shows the configuration of the phantom. The fixed yeast cells mixture was inserted into a 4 mm NMR tube that was inserted into an 8 mm glass sleeve filled with microcapillaries of 30±1 µm. This set-up was inserted into a 10 mm NMR tube.
Diffusion MRI experiments were conducted on a 14.1 T NMR spectrometer equipped with 3 T/m gradients. The pulsed-gradient-stimulated-echo (PGSTE) four shots EPI experiments were performed perpendicular (x-direction) and parallel (z-direction) to the main axis of the microcapillaries. One axial slice of 10 mm was acquired with the following parameters: matrix of 64×64 and FOV of 8.5×8.5 mm2 resulting in an in-plane resolution of 0.133×0.133 mm2, TR/TE=3000/25, Δ/δ=100/3.2, G= [5…905] mT/m (23 equal steps, qmax=123.3 mm-1) and NA=160. Note that the SNR's of the yeast cells and of the microcapillaries were ~70 and ~5, respectively.
Light microscopy was used to study the yeast cells' diameter distribution before the MRI sessions.
The MRI signal was processed by using pixel-by-pixel analysis as described previously3. The signal was modeled as a superposition of the MR signals arising from different restricted and free diffusing compartments3,6,7. Here, we assume that the restricted compartments have diameters in the range of 1-40 µm (50 steps) and a continued or a discrete weight distribution. Both fitting procedures were performed using three apparent diffusion coefficients (ADC) of 1.0·10-3, 1.5·10-3 and 2.0·10-3 mm2/s. No other assumptions were made.
Results and Discussion
Figure 2 shows the fractional diameter and free diffusion maps obtained by modeling the PGSTE MRI signals assuming two different weight distributions and two ADC values. It is clear that the sizes of both spherical and cylindrical compartments can be characterized accurately by both fitting procedures.
Significant populations of yeast cells were observed in both directions as expected from their spherical geometry. The yeast cells' average size that was extracted from the light microscopy is 5.00±0.36 µm, while the yeast cells' diameters that were extracted from the MRI signals are between 4 to 6 µm. For the fitted SDE signal of x-direction, the obtained mean sizes, assuming continued weight distribution, were 4.36±0.06 µm and 4.79±0.07 µm and the obtained mean sizes, assuming discrete weight distribution, were 4.48±0.06 µm and 4.86±0.07 µm, for ADC of 1.0·10-3 and 2.0·10-3 mm2/s, respectively.
As for the cylindrical compartment, a fraction of the diameters in the range of 29 to 31 µm appears in the area that corresponds to the location of the microcapillaries in the phantom only when diffusion was measured in the x-direction. In the z-direction, however, no notable populations are observed for the 29-31 µm diameters' range and only a free diffusing component is obtained there. These results match the excepted behavior of a compartment with cylindrical geometry.
A more detailed analysis of the results shows that the yeast cells can be characterized accurately by the model regardless of the assumed weight size distribution. The microcapillaries, however, are better characterized by the discrete weight distribution. Moreover, it seems that the ADC of 1.0·10-3 mm2/s is more suitable for the yeast compartment since for ADC of 2.0·10-3 mm2/s a significant fraction of yeast is observed when the diameters' range of 29 to 31 µm is inspected (Figure 2E). On the contrary, it seems that the ADC of 2.0·10-3 mm2/s is more suitable for the microcapillaries compartment (Figure 2Q).
Conclusions
This study shows that indeed a proper modeling of SDE MRI data provides accurate and detailed microstructural information. It also presents the great potential that the yeast cells- and microcapillaries-based phantom holds for validating of new models and methodologies aimed to extract detailed microstructural features of biological and neuronal tissues.Acknowledgements
No acknowledgement found.References
1. Jones DK. Diffusion MRI: theory, methods, and applications. New York: Oxford University Press, 2010.
2. Siow B, Drobnjak I, Chatterjee A, Lythgoe MF, Alexander DC. Estimation of pore size in a microstructure phantom using the optimised gradient waveform diffusion weighted NMR sequence. J. Magn. Reson. 2012 ; 215 : 51-60.
3. Morozov D, Bar L, Sochen N, Cohen Y. Modeling of the diffusion MR signal in calibrated model systems and nerves. NMR in Biomed. 2013; 26 (12) : 1787-1798.
4. Ning LP, Laun F, Gur Y, DiBella EVR, Deslauriers-Gauthier S, Megherbi T, Ghosh A, Zucchelli M ,Menegaz G, Fick R, St-Jean S, Paquette M, Aranda R, Descoteaux M, Deriche R , O'Donnell L, Rathi Y. Sparse Reconstruction Challenge for diffusion MRI: Validation on a physical phantom to determine which acquisition scheme and analysis method to use? Med. Image Anal. 2015; 1 : 316-331.
5. Morozov D, Bar L, Sochen N, Cohen Y. Microstructural information from angular double-pulsed-field-gradient NMR: From model systems to nerves. Magn. Reson. Med. 2015; 74 (1) : 25-32.
6. Grebenkov DS. NMR survey of reflected Brownian motion. Rev. Mod. Phys. 2007 ; 79(3) : 1077-1137.
7. Bar L, Sochen N. A spectral framework for NMR signal with restricted diffusion. Concepts Magn Reson (A). 2015; 44(1): 16-53.
Figures