3402
Orientation-invariant and non-parametric Axon Diameter Distribution mapping using PGSE and regularized discrete linear modeling1Signal Processing Laboratory 5 (LTS5), EPFL, Lausanne, Switzerland, 2Danish Research Centre for Magnetic Resonance, Center for Functional and Diagnostic Imaging and Research, Copenhagen University Hospital Hvidovre, Hvidovre, Denmark, 3Department of Applied Mathematics and Computer Science, Technical University of Denmark, Lyngby, Denmark, 4University Hospital Center (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 5Computer Science department, University of Verona, Italy
Synopsis
Axon diameter distributions (ADDs) change during brain development and are altered in several brain pathologies. Mapping ADDs non-invasively using dMRI could provide a useful biomarker, but existing methods are either parametric, orientation-dependent, summarize the whole ADD as a single measure or use non-standard protocols. We propose to estimate the ADD from an orientation-invariant PGSE protocol optimized for axon diameter sensitivity, using a discrete linear model with smoothness and sparsity regularization. To our knowledge, we are the first to show that PGSE sequences can be used to extract orientationally invariant and non-parametric ADD estimates.
Purpose
Axon diameters directly determine conduction speeds. Axon Diameter Distributions (ADDs) have been shown to vary during brain development and to be altered in several pathologies, hence impacting communication between brain regions. Several methods to map volume weighted ADDs non-invasively using dMRI have been proposed.1-3 Their main limitations are summarized it Table 1. Ideally, the method should be (i) sensitive to the whole ADD (reduction to a single parameter is less specific), (ii) non-parametric (parametric distributions might not be valid everywhere) and (iii) orientationally-invariant (no prior knowledge on the fiber orientation should be required). AMICO has recently been proposed as a framework for microstructure modeling using discrete linear models of the form $$$Ax=Y$$$, where $$$A$$$ is a dictionary of response functions, $$$x$$$ are the volume fractions of the elements of $$$A$$$ to be estimated and $$$Y$$$ is the acquired dMRI signal.4 Benjamini et al.3 showed that non-parametric ADD mapping is solvable through such a model. Because the problem is too ill-conditioned when PGSE protocols are used, they propose to use Double Diffusion Encoding (DDE) to reduce the ill-posedness of the problem. However, there are advantages in using an ADD mapping method based on PGSE, as the sequence provides orientational invariance with high angular resolution, and has been widely used and validated. Here, we use AMICO4 to implement a model for non-parametric ADD mapping based on an ActiveAx PGSE protocol optimized for axon diameter sensitivity.2 Accurate ADD reconstruction is achieved by combining smoothness and sparsity regularization to reduce the ill-posedness of the problem.Methods
Tissue model: similarly to the MMWMD model2 implemented in AMICO,4 we suppose the white matter is made of an intracellular (IC) compartment (modeled as a mixture of cylinders5) and an extracellular (EC) compartment (modeled as a mixture of zeppelins5).
Simulations: Simulations were split into $$$Y^{ec}$$$ and $$$Y^{ic}$$$. $$$Y^{ec}$$$ was simulated using Camino's Monte Carlo simulator,6 placing spins in the EC space of 1’000 impermeable cylinders with radii sampled from a gamma distribution ($$$k=3.50$$$, $$$\theta=3.26*10^-7$$$, IC volume fraction ICVF=0.73). Diffusivity was set to ($$$D_\parallel = 0.6x10^{-9} m^2/s$$$) and the protocol taken from Dyrby et al7 (ActiveAx optimized PGSE protocol, Gmax=300mT/m). The mean volume weighted diameter was 3.73 $$$\mu$$$m, which is above the resolution lower bound for the diameter index of this protocol.7 $$$Y^{ic}$$$ was computed analytically from the list of radii used in the Monte Carlo simulation, the final signal computed as $$$Y=ICVF*Y^{ic}+(1-ICVF)*Y^{ec}$$$, and contaminated with 100 rician noise realization corresponding to SNR = 30.
Intra-axonal reconstruction: We suppose that the ADD can be reconstructed by solving the discrete linear model $$$\min_{x^{ic} \geq 0}||A^{ic}x^{ic}-Y^{ic}||^2_2+\lambda_1 ||\Gamma x^{ic}||^2_2$$$,8 where $$$A^{ic}$$$ is a dictionary of cylinders5 with radii in [0.5, 7.0] um, $$$\Gamma$$$ introduces a smoothness penalty on coefficients $$$x^{ic}$$$ and $$$Y^{ic}$$$ is the intracellular dMRI signal.
Extra-axonal reconstruction: we
consider that the EC compartment can be recovered by solving: $$$\min_{x^{ec} \geq 0}||A^{ec}x^{ec}-Y||^2_2+\lambda_2\mathcal{R}(x^ {ec})$$$,
where $$$A^{ec}$$$ is a dictionary of zeppelins5 with $$$D_\perp \in [0.0,D_\parallel]$$$, $$$x^{ec}$$$ are the volume fractions to be
estimated, $$$Y^{ec}$$$ is the extacellular dMRI signal and $$$\mathcal{R}(x^ {ec})$$$ is a regularization term.
Full substrate reconstruction: the parameters of the full substrate were recovered by solving a problem of
the form $$$\min_{x \geq 0}||Ax-Y||^2_2+\lambda _1||\Gamma x^{ic}||^2_2 + \lambda _2\mathcal{R}(x^ {ec})$$$, where $$$A=[A^{ic}, A^{ec}]$$$, $$$x=[x^{ic},
x^{ec}]$$$ and $$$Y$$$ is the substrate dMRI signal. We explored different regularizations of the EC coefficients to address their
influence on the ADD estimation: (i) no
regularization, (ii) standard Tikhonov regularization: $$$\mathcal{R}(x^ {ec})=||x^{ec}||^2_2$$$ and (iii) sparsity regularization: $$$\mathcal{R}(x^ {ec})=||x^{ec}||_1$$$. In each experiment, $$$\lambda _1$$$ and $$$\lambda _2$$$ were
tuned to recover the ADD closest to the ground-truth.
Results and Discussion
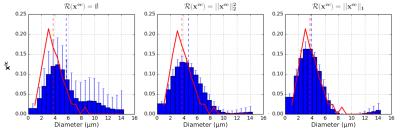
Results are summarized in Figure 1.
No regularization: the system fails to estimate the ADD and the mean volume weighted diameter.
Tikhonov regularization: recovered ADD and mean diameter estimates are closer to the ground-truth, although the shape of the ADD is wrong.
Sparse regularization: promoting sparsity yields the best results concerning both ADD reconstruction and the estimated mean diameter. Big diameters are slightly overestimated, likely because of their similarity with the EC signal.
Conclusion
Most ADD mapping methods are either parametric, summarize the ADD as a single index or use non-standard protocols like DDE. We proposed a method that uses smoothness and sparsity regularization to estimate ADDs from a standard optimized ActiveAx protocol based on PGSE. To our knowledge, these are the first reported results concerning an orientationally invariant ADD estimation. Future work will assess the performance of our method on data generated from other ground-truth distributions as well as from real data.Acknowledgements
No acknowledgement found.References
1. Assaf et al. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med. 2008;59:1347-1354
2. Alexander et al.
Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage. 2010;52(4):1374-1389
3. Benjamini et al. White matter microstructure from nonparametric axon diameter distribution mapping. Neuroimage. 2016;135:333-44
4. Daducci et al.
Accelerated Microstructure Imaging via Convex Optimization (AMICO) from diffusion MRI data. NeuroImage. 2015;105:32-44
5. Panagiotaki et al. Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage. 2012;59(3):2241-54
6. Hall and Alexander. Convergence and parameter choice
for Monte-Carlo simulations of diffusion MRI. IEEE Transactions on
Medical Imaging. 2009;28:1354-1364
7. Dyrby et al. Contrast and
stability of the axon diameter index from microstructure
imaging with diffusion MRI. Magn Reson Med. 2012;70:711-721
8. Romascano et al. Is it feasible to estimate rotation-invariant non-parametric axon diameter distributions from PGSE? Preliminary insights from regularized discrete linear modeling and simulated intra-axonal signals. ISMRM workshop on Breaking the Barriers of Diffusion MRI, Lisbon, 11-16 September 2016
Figures