3391
Validation of Sensitivity of Fast Kurtosis Measurements to Tissue Microstructural Changes1Center for Brain Imaging Science and Technology, Department of Biomedical Engineering, Zhejiang University, Hangzhou, People's Republic of China
Synopsis
Diffusional kurtosis imaging (DKI) is a significant extension of diffusion tensor imaging, providing sensitive biomarkers to diseases at the cost of lengthy acquisition and post-processing time. Fast DKI method operating with kurtosis tensor and based on axially symmetric approximation was then proposed to overcome the disadvantage. To explore the clinical utility of fast DKI, a Monte Calo simulation was conducted on a tissue model to validate the sensitivity of fast kurtosis measurements to four microstructural changes. The results suggest that fast DKI method is reliable with reduced scan time but considerable sensitivity to microstructural Changes frequently occurred in neurological diseases.
Purpose
Diffusion kurtosis imaging (DKI) is a promising extension of diffusion tensor imaging that enables quantification of non-Gaussian diffusion 1 , giving new insights into tissue microstructure and providing sensitive biomarkers in many diseases 2. However, lengthy acquisition and post-processing time hinder further clinical exploration of kurtosis imaging. Fast mean kurtosis (MK) method was then proposed requiring only 13 diffusion-weighted images 3 and 19 diffusion-weighted images with increased robustness 4 while two other critical DKI parameters, radial kurtosis (RK) and axial kurtosis (AK) have also been estimated with reduced data lately 5. Since the fast DKI method operates with kurtosis tensor and is based on axially symmetric approximation 5, we use Monte Calo simulation to test their sensitivity to tissue microstructural changes to explore the clinical utility of fast DKI.Method
Conventional DKI (CDKI) method uses two b value and 30 directions, with a total of 61 diffusion weighted images including b0 image, to fit the signal equation (1) in Table 1 to get the 21 unknowns of diffusion tensor and kurtosis tensor, enabling the estimation of mean and directional kurtosis defined in (2) of Table 1. Fast DKI (FDKI) makes use of mathematically more convenient kurtosis tensor $$$W(\widehat{n})$$$ to define fast kurtosis parameters in line (4) in Table 1. The new definitions enable direct computation of $$$\overline{W}$$$ from diffusion signal along nine determined directions, and $$$W_{\perp}$$$ from 4 directions, $$$W_\parallel$$$ from 1 direction if the principle diffusion direction is known. Even though only in regions like spinal cord or peripheral nerve the principal direction of images is a priori knowledge, approximating axial symmetry of diffusion and kurtosis tensor allows the new signal equation be written as (3) in Table1, reducing the unknowns to only 8, thus enabling a fast determination of DKI parameters by nonlinear fitting to the 19 measurements acquired with 199 protocol 4.
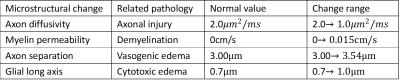
To explore the validity of sensitivity of fast kurtosis parameters to tissue microstructural changes and compare it to the conventional ones, we adopted a tissue model containing axons, glial cells, and extra-axonal space 6. The axon and the glial cell were modeled by cylinder and ellipsoid respectively and a hexagonal shape was chosen as the basic unit for its more efficient use of space as shown in Figure 1. Four microstructural changes leading to certain pathologies frequently appeared in TBI, stroke, glioma or neurodegenerative diseases were simulated as shown in Table 2. 6-9 Simulations contain a group of 1.2×105 particles. Axon radius/glial cell short axis is 1/0.7μm resulting to axon/glial fraction of 40.31% /14.75% at normal state. Extra-axonal diffusivity is 2μm2/ms and glial membrane permeability is 0.001cm/s. The diffusion process was discretized by separating the diffusion time D (50ms) into T (10000) steps, and diffusion-weighted signal was synthesized following the time evolution of the pulsed gradient spin echo sequence. Signals of b=1000, 2600s/mm2 from 9 directions for FDKI estimation and 30 equally spaced directions for CDKI are simulated. A nonlinear fit was used for both fast and conventional DKI.
Results & Discussion
The results are shown in Figure 2. FDKI parameters show the same tendency as conventional ones in all simulated changes. In axonal injury simulation, with the axon diffusivity decreasing, FDKI parameters is less sensitive than CDKI parameters (AKf decreased 22.2% verse AKc decreased 35%, MKf increased 11.8% verses MKc increased 24.7%), and RK is nearly unchanged, which is in line with the result in the stroke study 7, reporting an intra-axonal diffusivity decrease leading to a more sensitive change in AK than MK and RK. In demyelination, all kurtosis parameters shows a decrease consistent with a cuprizone mouse model study 8, while fast DKI performs better with MK and RK being comparable and AKf shows a much higher sensitivity (-94.6% verses -27.4%). For vasogenic edema the extent of changes in MK is nearly the same while RKf is less sensitive (-19.5% verses -33.6) and AKf is more sensitive (-41.4% verse -24.5%). The performance in cytotoxic edema is comparable in all parameters with AK being the most sensitive one. The overall results suggest that fast estimation of DKI parameters is in general as sensitive and reliable as conventional DKI, while reducing the whole brain DKI scan to 2 minutes.Conclusion
In this work, a simulation study of tissue microstructural changes was conducted to explore the sensitivity of fast and conventional DKI parameters, validating that fast kurtosis method can be reliable with reduced scan time but retains considerable sensitivity to many microstructural changes that occur in neurological diseases.Acknowledgements
No acknowledgement found.References
1. Jensen J H, Helpern J A, Ramani A, et al. Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 2005; 53(6): 1432-1440.
2. Steven A, Zhuo J, Melhem E R, et al. Diffusion Kurtosis Imaging: An Emerging Technique for Evaluating the Microstructural Environment of the Brain. American Journal of Roentgenology, 2013; 202(1).
3. Hansen B, Lund T E, Sangill R, et al. Experimentally and computationally fast method for estimation of a mean kurtosis. Magnetic Resonance in Medicine, 2013; 69(6): 1754-1760.
4. Hansen B, Lund T E, Sangill R, et al. Experimental considerations for fast kurtosis imaging. Magnetic Resonance in Medicine, 2015.
5. Hansen B, Shemesh N, Jespersen S N, et al. Fast imaging of mean, axial and radial diffusion kurtosis. NeuroImage, 2016.
6. Lin M, He H, Schifitto G, et al. Simulation of changes in diffusion related to different pathologies at cellular level after traumatic brain injury. Magnetic Resonance in Medicine, 2015; 76(1): 290-300.
7. Hui E S, Fieremans E, Jensen J H, et al. Stroke Assessment With Diffusional Kurtosis Imaging. Stroke, 2012; 43(11): 2968-2973.
8. Raab P, Hattingen E, Franz K, et al. Cerebral Gliomas: Diffusional Kurtosis Imaging Analysis of Microstructural Differences. Radiology, 2010; 254(3): 876-881.
9. Falangola M F, Guilfoyle D N, Tabesh A, et al. Histological correlation of diffusional kurtosis and white matter modeling metrics in cuprizone-induced corpus callosum demyelination. NMR in Biomedicine, 2014; 27(8): 948-957.
Figures