3388
Phase retrieval from q-space imaging for diffusion pore imaging1Medical Physics in Radiology, Deutsches Krebsforschungszentrum (DKFZ, German Cancer Research Center), Heidelberg, Germany, 2Institute of Radiology, University Hospital Erlangen, Erlangen, Germany, 3Electrical Engineering & Information Technology, Karlsruhe University of Applied Science, Karlsruhe, Germany
Synopsis
Diffusion pore imaging enables the detection of the average shape of arbitrary closed pores in an imaging volume element. Until now, an experimentally challenging phase measurement, either by measuring with a long-narrow gradient profile or by employing double diffusion encodings, was a prerequisite to obtain the full information on the Fourier transform of the pore image. In this study, we present a first experiment, where the phase information is recovered alone from the magnitude information acquired by q-space imaging. To solve this phase problem, we adopted a phase retrieval algorithm that is widely applied to X-ray diffraction data.
Introduction
Diffusion pore imaging allows determining the shape of arbitrary closed pores filled with an NMR-detectable medium, for example cells in biological tissue. The initial diffusion pore imaging approach measures the full Fourier transform of the pore space function: Both signal magnitude and phase are obtained by applying a long-narrow gradient profile1-5. Alternatively, q-space imaging which provides the magnitude information6,7 can be combined with double diffusion encoded measurements from which the phase can be extracted8,9. While the first method is quite inflexible in its sequence design, the second shows instabilities in the phase reconstruction at large q-values. Measuring phases in MRI is often difficult, especially in vivo. Here, we propose an alternative approach that does not require a phase measurement:
The purpose is to recover the pore space function $$$\rho(\boldsymbol{x})$$$ alone from the magnitude measurement of its Fourier transform $$$\left|\tilde{\rho}(\boldsymbol{q})\right|$$$. In other words: To retrieve the phase of $$$\tilde{\rho}(\boldsymbol{q})$$$ from q-space measurements $$$S_{11}(\boldsymbol{q})=\left|\tilde{\rho}(\boldsymbol{q})\right|^2$$$.
Theory
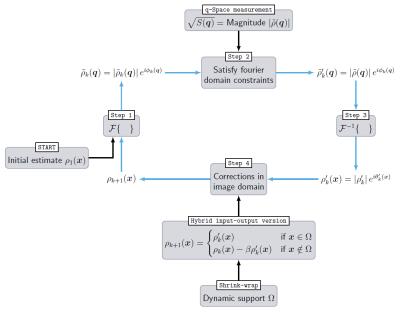
This phase problem is solved with an iterative algorithm that is commonly applied to analogous problems in many different fields of physics10, such as X-ray diffraction. As the basic assumption enabling phase retrieval, we use that the pore image size is finite and therefore $$$\rho(\boldsymbol{x})$$$ is zero outside the pore boundary $$$\Omega$$$. $$$\Omega$$$ is found during the course of the phase retrieval by thresholding the reconstructed image11. The scheme of the algorithm is illustrated in Fig. 1.
First, the magnitude of the Fourier transform of $$$\rho(\boldsymbol{x})$$$, denoted as $$$\left|\tilde{\rho}(\boldsymbol{q})\right|$$$, is obtained from the q-space imaging signal $$$S_{11}(\boldsymbol{q})=\left|\tilde{\rho}(\boldsymbol{q})\right|^2$$$ where $$$q=\gamma\boldsymbol{G}\delta$$$ is the q-space vector with gradient pulse amplitude $$$\boldsymbol{G}$$$, duration $$$\delta$$$ and gyromagnetic ratio $$$\gamma$$$. Inside the pore, $$$\rho(\boldsymbol{x})$$$ is equal to (pore volume)-1, and outside $$$\rho(\boldsymbol{x})=0$$$ is valid. The algorithm is started by creating a two-dimensional guess of the pore image in x-space with pixels of constant magnitude and random phase in $$$\left[0,\frac{\pi}{2}\right]$$$. Now, the algorithm iterates in four steps between q-space and x-space12 (Fig. 1, blue arrows):
Step 1: In iteration $$$k$$$, Fourier transforming the estimate of the pore image yields:$$$\tilde{\rho}_k(\boldsymbol{q})=\left|\tilde{\rho}_k(\boldsymbol{q})\right|\exp\left[i\phi_k(\boldsymbol{q})\right]=\text{FT}\left\{\rho_k(\boldsymbol{x})\right\}$$$.
Step 2: The current estimated Fourier magnitude is replaced with the measured magnitude $$$\left|\tilde{\rho}(\boldsymbol{q})\right|$$$: $$$\tilde{\rho}_k^\prime(q)=\left|\tilde{\rho}(\boldsymbol{q})\right|\exp\left[i\phi_k(\boldsymbol{q})\right]$$$.
Step 3: An inverse Fourier transform is performed:$$$\rho^\prime_k(\boldsymbol{x})=\left|\rho^\prime_k(\boldsymbol{x})\right|\exp\left[i\theta^\prime_k(\boldsymbol{x})\right]=\text{FT}^{-1}\left\{\rho_k^\prime(\boldsymbol{q})\right\}$$$.
Step 4: The new estimate of the pore image is formed by modifying $$$\rho^\prime_k(\boldsymbol{x})$$$ to satisfy the image-domain constraint, i.e. satisfying the support $$$\Omega$$$. In the hybrid input-output13 (HIO) version, the next input image is formed by adopting $$$\rho^\prime_k(\boldsymbol{x})$$$ inside $$$\Omega$$$ and suppressing the outer image region by driving it close to zero: $$\quad\rho_{k+1}(\boldsymbol{x})=\begin{cases}\rho^\prime_k(\boldsymbol{x})&\;\text{if}\;\;\boldsymbol{x}\in\,\Omega\\\rho_k(\boldsymbol{x})-\beta\rho^\prime_k(\boldsymbol{x})&\;\text{if}\;\;\boldsymbol{x}\notin\,\Omega\text{,}\end{cases}$$ with feedback constant $$$0\leq\beta\leq1$$$.
Continue with step 1.
Methods
On a clinical 1.5 T MR-scanner (Magnetom Symphony; Siemens), the q-space imaging signal was measured for a phantom with 170 pores of equilateral triangular shape (3.4 mm edge length) which were filled with hyperpolarized Xe-129 gas that was generated by spin exchange optical pumping. 37 radial spokes in q-space were recorded with 9 q-values each ($$$\delta$$$=3.36 ms, diffusion time 270 ms, maximal q-value 8 mm-1).
$$$\left|\tilde{\rho}(\boldsymbol{q})\right|$$$ was interpolated by a factor of 2 through zero padding its Fourier transform and then Fourier transforming back to q-space14. A first loose support was determined by thresholding the autocorrelation function $$$A(\boldsymbol{x})=\text{FT}^{-1}\left[\left|\tilde{\rho}(\boldsymbol{q})\right|^2\right]=\text{FT}^{-1}\left[S_{11}(\boldsymbol{q})\right]$$$ at 8 %. Every 6 iterations, $$$\Omega$$$ was improved using the shrink-wrap method: By thresholding the Gaussian-filtered modulus of the latest reconstructed image at 24 %, a new support is found that shrinks from update to update until it encloses the actual pore shape tightly11. The width of the Gaussian, initially σ=1.5 pixels, was reduced at each update by 3 %.
72 iterations of the HIO algorithm with $$$\beta$$$ = 0.9 were performed.
Results
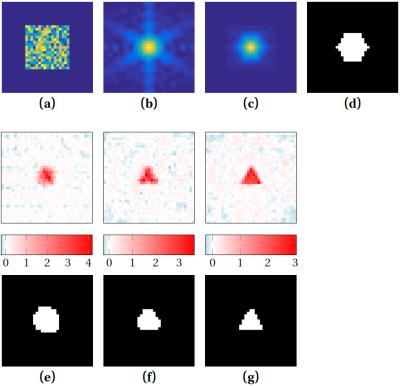
The phase retrieval procedure is depicted in Fig. 2: (a) To (d) show the information that went into the algorithm. (e) To (g) show the reconstructed pore image at different iterations and the corresponding supports boundaries: A steady improvement in the pore boundary can be observed and after iteration 72 in (g), the pore image shows a clearly discernible equilateral triangle. Sometimes, the boundary tends to over-shrink as in (f), but recovers most often as shown from (f) to (g).Discussion
This experiment demonstrates that phase retrieval from q-space imaging data is feasible so that complicated phase measurements as in 1-5,8,9 might not be required in certain cases. Further, this global reconstruction approach has the potential to yield better phase stability than the double diffusion encoded approach9, where phase reconstruction is performed individually for each spoke in q-space. This will require further testing on different pore shapes and on distributions of pore shapes and sizes.Acknowledgements
Financial support by the DFG (grant no. KU 3362/1-1 and LA 2804/2-1) is gratefully acknowledged.
References
1) Laun FB, Kuder TA et al., Determination of the defining boundary in nuclear magnetic resonance diffusion experiments, Phys. Rev. Lett. 107, 048102 (2011).
2) Laun FB, Kuder TA et al., NMR-based diffusion pore imaging, Phys. Rev. E 86, 021906 (2012).
3) Kuder TA, Bachert P et al., Diffusion pore imaging by hyperpolarized Xenon-129 nuclear magnetic resonance, Phys. Rev. Lett. 111, 028101 (2013).
4) Hertel S, Hunter M et al., Magnetic resonance pore imaging, a tool for porous media research, Phys. Rev. E 87, 030802 (2013).
5) Hertel SA, Wang X et al., Magnetic-resonance pore imaging of nonsymmetric microscopic pore shapes, Phys. Rev. E 92, 012808 (2015).
6) Cory DG and Garroway AN, Measurement of translational displacement probabilities by NMR: an indicator of compartmentation, Magn. Reson. Med. 14, 435-444 (1990).
7) Callaghan PT, Coy A et al., Diffraction-like effects in NMR diffusion studies of fluids in porous media, Nature (London) 351, 467 (1991).
8) Shemesh N, Westin CF et al., Magnetic resonance imaging by synergistic diffusion-diffraction patterns, Phys. Rev. Lett. 108, 058103 (2012).
9) Kuder TA and Laun FB, NMR-based diffusion pore imaging by double wave vector measurements, Magn. Reson. Med. 70, 836-841 (2013).
10) Fienup JR, Phase retrieval algorithms: a personal tour [Invited], Appl. Opt. 52, 45-56 (2013).
11) Marchesini S, He H et al., X-ray image reconstruction from a diffraction pattern alone, Phys. Rev. B 68, 140101(R) (2003).
12) Gerchberg RW and Saxton WO, A Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures, Optik 35, 237 (1972).
13) Fienup JR, Reconstruction of an object from the modulus of its Fourier transform, Opt. Lett. 3, 27-29 (1978).
14) Miao J and Sayre D, On possible extensions of X-ray crystallography through diffraction-pattern oversampling, Acta Crystallogr. A 56, 596-605 (2000).
15) Fienup JR and Wackerman CC, Phase-retrieval stagnation problems and solutions, J. Opt. Soc. Am. A 3, 1897-1907 (1986).
Figures