3385
Effect of Realistic Timing Parameters on a Microscopic Diffusion Anisotropy Measure1Department of Systems Neuroscience, University Medical Center Hamburg-Eppendorf, Hamburg, Germany, 2Neuroimage Nord, University Medical Centers Hamburg-Kiel-Lübeck, Hamburg-Kiel-Lübeck, Germany
Synopsis
Double diffusion encoding experiments with two weighting periods applied successively offer access to microscopic tissue properties and can provide information complementary to diffusion tensor imaging. The MA index derived from such measurements with long mixing times, depends on the cell eccentricities, i.e. the microscopic diffusion anisotropy, and can be determined in the human brain. However, its derivation is based on ideal timing parameters, infinitely short gradient pulses and long diffusion and mixing times that cannot be gained in practice. In this study, the effect of realistic timing parameters on the MA of restricted diffusion is investigated with Monte Carlo simulations.
Introduction
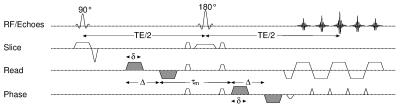
The investigation of tissue microstructure with double diffusion encoding (DDE) or double wave vector experiments (Fig.1) in that two diffusion weighting periods are applied successively in a single acquisition, have gained increasing interest in the past years [1-6]. With long mixing times τm between the two weightings, the experiment offers access to the cell eccentricity, i.e. the diffusion anisotropy on a microscopic scale, and, inter alia, could detect anisotropic diffusion even in regions that appeared isotropic in diffusion tensor imaging [7]. Recent studies have shown that a measure of the microscopic diffusion anisotropy, the MA index [8], can be determined in white and gray matter in the living human brain [9, 10]. However, the MA is based on the assumption of ideal timing parameters, infinitely short gradient pulses, infinitely long diffusion and mixing times that cannot be gained on whole-body MR systems. In this study, the effect of realistic timing parameters of restricted diffusion on the MA is investigated with Monte Carlo simulations. Methods
Monte
Carlo simulations were performed with an in-house developed algorithm
written in IDL 8.3 (ITT Visual Information Solutions, Boulder, CO,
USA). The random walk of 50,000 particles was simulated in 200
isolated, restricted geometries such as cylinders and ellipsoids with
dimensions between 3-50 μm that can be considered to represent
typical white and gray matter structures, respectively, visible in
diffusion-weighted experiments of the human brain. The MR signals for
the 96 diffusion weighting directions used for the determination of
the MA index [8] were calculated and fitted to the corresponding
tensor
equation using a Levenberg-Marquard algorithm to determine the MA. In
a first setup (“short-pulse”), realistic parameters were
considered for the diffusion and mixing times only (Δ 40 ms,
τm
25 ms) but not for the gradient pulse duration (δ 1 µs);
in the second setup (“whole-body”),
δ also had a realistic duration (22 ms) aiming at the
timing parameters typically used on a whole-body MR system (Δ
28 ms, τm
25 ms).
The MA values obtained with both setups (“short
pulse”,“whole-body”)
were
compared to the
ground-truth values that can be derived from the restricted geometry.
Results and Discussion
Results
of the Monte Carlo simulation with the corresponding fits for the
“short pulse”
setup
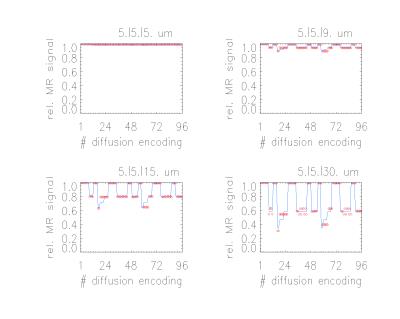
are sketched in Fig. 2 for four prolate geometries (short
axis 5 µm, long axes 5.0, 9.0, 15.0 and 30.0 µm, respectively) and
a full set of the diffusion encoding directions showing a good agreement of
(i) the fit (lines) with the simulated signals (symbols)
and (ii) of the derived MA values with the real ones. In
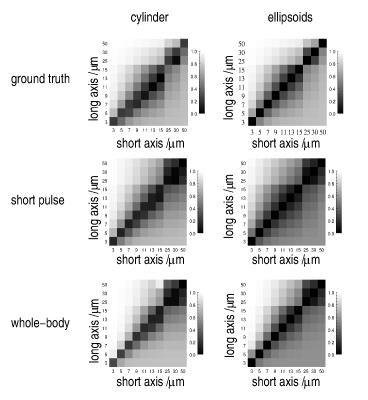
general, the ground-truth MA for cylindrical and ellipsoidal
geometries of various dimensions coincide very well with the results
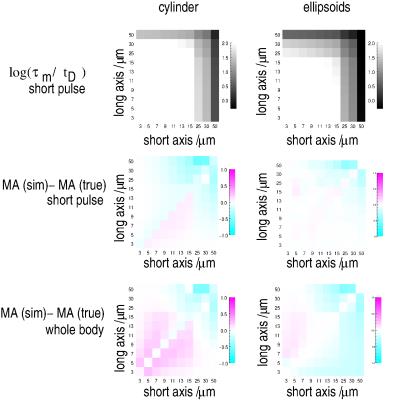
derived from both setups (Fig. 3). Nevertheless,
slight systematic differences can be revealed between simulated and
ground truth parameters as shown in Fig. 4. Considering the time tD
a
spin typically needs to cross a pore, two different regimes can be
distinguished: for the central part of th;e plots, Δ, τm
>>
tD,
i.e. the diffusion and mixing times are close to ideal, yielding
only minor deviations of the MA from the ground truth. For the outer
parts, τm
and Δ are on the order of tD
or approach it which violates the assumption of ideal timing
parameters
significantly and results in more pronounced, systematic deviations
of the MA. For the “short pulse” setup, deviations occur for
large geometry dimensions and always cause an underestimation of the MA
because the spin displacements are lower than for ideal timings. This
is similar to the “whole-body” setup, however, it also reveals an
overestimation of the MA for smaller dimensions
which most likely, is related to the center-of-mass effect for finite
pulse durations [11] that effectively yields an underestimation
of smaller dimensions. Both setups perform very well for the
isotropic pores on the plot’s diagonal since any over- or
underestimation is identical for both dimensions and cancels out.
Conclusion
In summary, the simulations can be well approximated by the DDE tensor model underlying the MA definition and the MA values show only minor deviations from the ground-truth values, even for the non-ideal timing parameters required on a whole-body MR system.Acknowledgements
No acknowledgement found.References
[1] Mitra P, Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement. Phys. Rev. B 51, 15074 (1995)
[2] Shemesh N, Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn. Reson. Med. 75, 82 (2015)
[3] Cheng Y, Multiple Scattering by NMR, J. Am. Chem. Soc. 121, 7935 (1999)
[4] Özarslan E, Compartment shape anisotropy (CSA) revealed by double pulsed field gradient MR. J. Magn. Reson. 199, 56 (2009)
[5] Koch M, Towards compartment size estimation in vivo based on double wave vector diffusion weighting. NMR Biomed. 24, 1422 (2011)
[6] Koch M, Numerical simulation of double-wave vector experiments investigating diffusion in randomly oriented ellipsoidal pores. Magn. Reson. Med. 62, 247 (2009)
[7] Lawrenz M, Double-wave-vector diffusion-weighted imaging reveals microscopic diffusion anisotropy in the living human brain. Magn. Reson. Med. 69, 1072 (2013)
[8] Lawrenz M, A tensor model and measures of microscopic anisotropy for double-wave-vector diffusion-weighting experiments with long mixing times. J. Magn. Reson. 202, 43 (2010)
[9] Lawrenz M, Microscopic diffusion anisotropy in the human brain: reproducibility, normal values, and comparison with the fractional anisotropy. Neuroimage 109, 283 (2015)
[10] Lawrenz M, Detection of Microscopic Diffusion Anisotropy in Human Brain Cortical Gray Matter in Vivo with Double Diffusion Encoding. Proc. ISMRM 2016, p. 212
[11] Mitra P, Effects of Finite Gradient-Pulse Widths in Pulsed-Field-Gradient Diffusion Measurements. J Magn. Reson. A 113, 94 (1995)
Figures