3383
Double Diffusion Encoding vs Single Diffusion Encoding in Parameter Estimation of Biophysical Models in Diffusion-Weighted MRISantiago Coelho1, Leandro Beltrachini1,2,3, Jose M. Pozo1, and Alejandro F. Frangi1
1Centre for Computational Imaging & Simulation Technologies in Biomedicine (CISTIB), Department of Electronic and Electrical Engineering, The University of Sheffield, Sheffield, United Kingdom, 2School of Physics and Astronomy, Cardiff University, Cardiff, United Kingdom, 3Cardiff University Brain Research Imaging Centre (CUBRIC), Cardiff University, Cardiff, United Kingdom
Synopsis
Biophysical tissue models are a solid tool for obtaining specific biomarkers with diffusion MRI. However, the assumptions they rely on are sometimes inaccurate and may lead to erroneous results. Some limitations of the Neurite Orientation Dispersion and Density Imaging (NODDI) model are tackled by NODDIDA (NODDI with Diffusivities Added), at the cost of an extended acquisition protocol. Here we adapt NODDIDA to a Double Diffusion Encoding scheme to improve the parameter estimation for reduced acquisition protocols. We demonstrate through in silico experiments that under similar experimental conditions, this novel approach increases both the accuracy and precision of the parameter estimates.
Background
Diffusion MRI has been established as an invaluable tool for characterising brain white matter (WM) in vivo and non-invasively. The quest for specific biomarkers on tissue integrity encouraged the development of biophysical models1-3. By assuming certain characteristics on tissue properties (such as geometry and diffusivities), these models allow us to extract more specific information than phenomenological approaches (e.g. DTI). However, to provide accurate estimations, biophysical models usually require extensive data acquisition protocols, limiting their applicability in the clinic. In addition, new protocols for diffusion MRI acquisition are emerging such as Double Diffusion Encoding (DDE)4, which have not been fully explored in this context. In the NODDI2 model, diffusivities are fixed to certain values. This allowed reducing the acquisition protocol, but at the expense of introducing bias in the estimated parameters. NODDIDA3 tackles this problem by releasing the diffusivities in the estimation process. However, this introduced a degeneracy problem in the parameter estimation, which is only solved if the acquisition protocol is extended from 60 to 120 directions.Purpose
To show the feasibility of applying DDE biophysical models and expose their advantages over SDE in terms of improved parameter estimation for reduced acquisition protocols.Methods
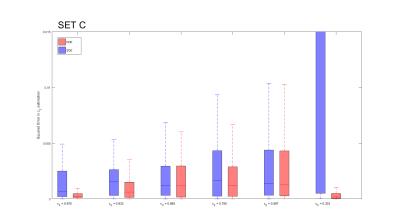
We adapted the NODDIDA model to a DDE scheme. This adds more degrees of freedom to the data acquisition protocol (i.e. two diffusion encoding periods must be chosen). The dependence of the model’s signal attenuation on the sequence parameters is the same for Single Diffusion Encoding (SDE) and DDE with parallel gradients. Thus, under the same experimental conditions (e.g. directions, b-values, etc.), both protocols will lead us to the same parameter estimates. Alternatively, the signal arising from a DDE experiment with perpendicular gradient directions provides a different dependence on the sequence parameters. Therefore, we hypothesised that DDE sequences with parallel and perpendicular acquisitions will outperform SDE in informing biophysical models. To test this hypothesis, we generated the same amount of in silico data for both protocols (i.e. SDE and DDE with parallel and perpendicular acquisitions) and performed two experiments. We considered 60 non-collinear directions5 divided into two shells3 with b-values of 1 and 2 ms/μm2. The ground truth parameter sets for the first experiment were taken from 3 and consisted of two possible solutions of the NODDIDA model for a voxel of the posterior limb of the internal capsule (PLIC). For the second experiment, we selected diffusivities in accordance with NODDI’s assumptions together with multiple fibre dispersion values. The substrates were composed of 1μm radius cylinders. Rician noise6 was added to the simulated data, resulting in a signal-to-noise ratio (SNR) of 50 for SDE3. Transverse relaxation effects were considered and, as the echo time in DDE is 20% larger, this amounts to an SNR 15% lower. The optimisation was performed with the fitting procedures used in 2 and 3, and both led to similar results.Results
Considering similar experimental conditions (e.g. scanning time available), in silico experiments show a reduction in the mean squared error of the estimates in the case of using the DDE scheme. Figure 1 shows the histograms for the estimated model parameters in the first experiment. The bi-modal distribution of the estimated parameters is evident in the case of using the SDE sequence. This effect is mitigated when using the DDE sequence, as shown in the bottom row of Figure 1. Figure 2 shows that the error using the DDE scheme is also lower for the case of a different substrate with various dispersion values.Discussion
The experiments show that by modifying the acquisition protocol we may be able to solve the degeneracy on NODDIDA’s parameter estimation. This would avoid having to fix the diffusivities to a priori values as done in NODDI. Furthermore, it would allow not only to capture the biological variability of the diffusivities across WM tissue but also to reduce the mean squared error in the estimation of the remaining model parameters. In addition, an optimised DDE protocol is still to be developed to maximise the performance of this sequence in the extraction of microstructural information.Conclusion
We extended NODDIDA from a SDE to a DDE scheme. This proved to be beneficial for increasing the accuracy of the parameter estimation given a set of noisy measurements. Moreover, it does not require an extensive data acquisition to obtain acceptable results. Novel diffusion MRI sequences should be tested in terms of their efficiency to extract information from a modelling approach. Even mixed protocols containing measurements from different sequences may be optimal. Further work will include a comprehensive analysis including human measurements.Acknowledgements
This work has been supported by the OCEAN project (EP/M006328/1) funded by the Engineering and Physical Sciences Research Council (EPSRC).References
1. Assaf Y, Basser PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage. 2005;27:48-58.
2. Zhang H, Schneider T, Wheeler-Kingshott CA, et al. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012;61:1000-1016.
3. Jelescu IO, Veraart J, Fieremans E, et al. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed. 2016;29:33-47.
4. Shemesh N, Jespersen SN, Alexander DC, et al. Conventions and Nomenclature for Double Diffusion Encoding NMR and MRI. Magn. Reson. Med. 2015;75:82-87.
5. Koay CG, Özarslan E, Johnson KE, et al. Sparse and optimal acquisition design for diffusion MRI and beyond. Med. Phys. 2012;39(5):2499-2511.
6. Gudbjartsson H, Patz S. The Rician Distribution of Noisy MRI Data. Magn. Reson. Med. 1995;34(6):910-914.
Figures
Figure 1. Histograms of the estimated model parameters for SDE (top row) and DDE (bottom row) schemes in the first experiment for 1500 independent noise realisations. The ground truth represents two different possible solutions of the NODDIDA model applied to a voxel in the PLIC3. These values are shown in red lines and correspond to set A (fi=0.38; Di=0.50 μm2/ms; De,||=2.10 μm2/ms; De,﬩=0.74 μm2/ms; c2=0.98) on the left, and set B (fi=0.77; Di=2.23 μm2/ms; De,||=0.16 μm2/ms; De,﬩=1.48 μm2/ms; c2=0.70) on the right. The sequence parameters used were: 𝛿=12.9ms, ∆=21.8ms in SDE, and 𝛿= τm=9ms, ∆=14ms in DDE.
Figure 2. Boxplots showing the squared error for the estimated c2 values in the second experiment with 100 independent noise realisations. The water fraction and diffusivities were chosen in accordance with NODDI’s assumptions of human in vivo tissue (set C: fi=0.55; Di=1.7 μm2/ms; De,||=1.7 μm2/ms; De,﬩=0.765 μm2/ms). Different values of coherence between fibres (c2) were considered. The box corresponding to the lower c2 in SDE is larger due to a bi-modal distribution and exceeds the range of the y-axis. The SDE and DDE protocols were the same as in the first experiment.