3380

Axon diameter mapping using diffusion MR microscopy embedded in a Monte-Carlo based fingerprint approach
Delphine Estournet1,2, Justine Beaujoin1,2, Fabrice Poupon2,3, Achille Teillac1,2, Jean-François Mangin2,3, and Cyril Poupon1,2

1CEA/I²BM/NeuroSpin/UNIRS, Gif-sur-Yvette, France, 2Université Paris-Saclay, Orsay, France, 3CEA/I²BM/NeuroSpin/UNATI, Gif-sur-Yvette, France

Synopsis

In this work, we demonstrate that Monte-Carlo simulations combined with fingerprint approaches can be used to develop decoding tools of the micro-structure using a dictionary learning approach. The validation has been done on a test object mimicking the mid-sagittal plane of a corpus callosum with axon diameters varying according to histological studies. The robustness of the decoding obviously depends on the richness of the dictionary, but, contrary to analytical approaches with highly non linear equations hard to fit practically, such MC approach do not have this kind of limitation, thus opening the way to decode more complex tissue cellular configurations.

Purpose

Diffusion magnetic resonance imaging (dMRI) is a powerful tool to characterize the microstructure of brain white matter, especially the axon diameter/density. Current techniques1,2,3,4 rely on analytical models of the DW signal used to decode the axon diameter/density. Today, models are limited to simple impermeable cylinder geometries because of the high non-linearity of the corresponding equations. To go beyond, we propose an alternative approach based on Monte-Carlo simulations combined with machine learning tools using a dictionary of simulated geometries to decode the microstructure, and we demonstrate that it is as efficient as analytical models to map the axon diameter/density within white matter.

Methods

A dedicated framework was developed to assess the feasibility of quantitative axon mapping using a Monte-Carlo approach similar, considering the geometries, to the original ActiveAx1 method proposed in the Camino5 toolkit, eg impermeable parallel cylinders without angular dispersion in the case of this study.

Dictionary of patterns - 63 geometries of impermeable parallel cylinders with various cylinder diameter (1-10µm) and separated with various spacings (0 to the cylinder diameter) were designed and saved using triangulated surfaces (Fig1).

Monte-Carlo (MC) simulations – the Diffusion Microscopist Simulator (DMS)6 was used to simulate the Brownian motion of water molecules within each of the former 63 geometry patterns (Fig1). For each configuration, 1000 simulations were performed.

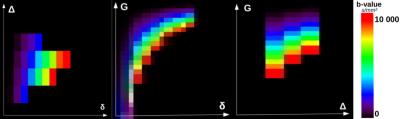
DW signal simulations – the diffusion-decay values corresponding to various settings of a single Pulsed-Gradient Spin Echo sequence were also computed using the DMS tool, but, unlike current ActiveAx protocols (4 different diffusion schemes/shells with specific b-values/diffusion times), and because no scan duration imposes this drastic simplification of the imaging protocol when using simulation, we established a novel strategy based on a Cartesian sampling of the (δ,∆,G) space limited by the MRI system hardware capabilities. For each (δ,∆,G) setting, the diffusion-decay was simulated along 500 diffusion orientations uniformly distributed over the sphere of corresponding b-values. Because we aim at validating our proposed framework on a ex vivo sample of corpus callosum, we used the hardware constraints of a preclinical 11.7T Bruker MRI system, and imposed b (100<= b<=10000s/mm2), G (Geffective<=0,7*Gmax=532mT/m) and TE (<=60ms) constraints. In total, 343 settings stemming from 10δ/4∆/25G/4TE were used (Fig2).

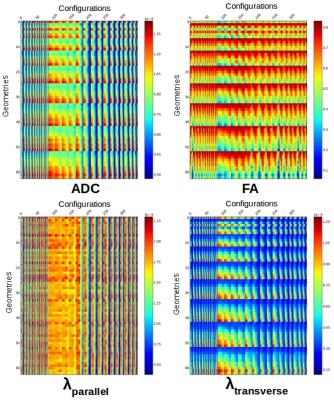
Dictionary of signatures – because the underlying geometry corresponds to homogeneous populations of parallel cylinders, the 500 diffusion decays for each (δ,∆,G) setting could be reduced to their associated DTI coefficients, without loss of information. Of course, for more complex geometries, higher angular models should be used like the SHORE6 decomposition of propagator for instance. This reduction of the problem yielded a resulting matrix corresponding to a dictionary of diffusion-decay signatures for each of the 63 simulated geometries (Fig3).

Decoding of the geometry – this dictionary allowed to construct a decoding tool to automatically recognize the geometry pattern from the observation of its signature established from a collection of DW MR acquisitions. To this aim, a Support Vector Machine7 supervised classifier was trained from the simulated data using the former dictionary.

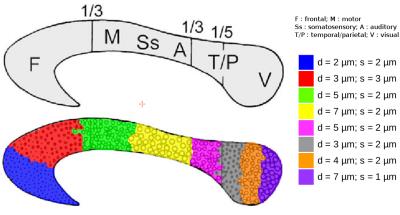
Synthetic corpus callosum test sample – a test object was created to mimic the mid-sagittal plane of a corpus callosum (white matter fibers depicting geometrical configurations close to what was simulated) with axon diameters/spacings set according to histological studies8 (Fig4).


Results & Discussion

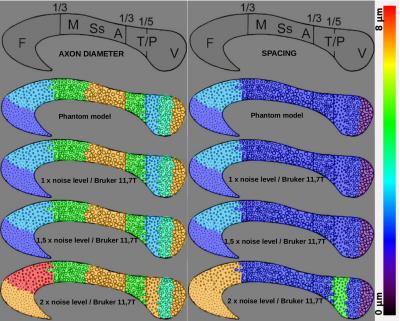
MC simulations were computationally intensive for the 63 geometries (~2 months on a workstation with 40 CPU cores/80 threads with 256GB of memory) but needed to be evaluated only once (Fig1). Figure 2 represents the true domain of available (δ,∆,G) configurations that respects the 11.T Bruker MRI system hardware constraints, the target millimeter resolution constraint and the maximum b, G and TE contraints. The dictionary matrix showing the variation of parameters according to the diffusion sensitization settings and the geometries assessed the feasibility to distinguish the geometry using such information with a supervised classifier (Fig3). As expected, with the designed synthetic corpus callosum (Fig4), the decoding tool was able to recognize the underlying geometry and remains efficient up to twice the standard noise level, the overestimation errors being of the same kind as those found using ActiveAx (Fig5).

Conclusion

In this work, we demonstrated that Monte-Carlo simulations are useful to develop decoding tools of the micro-structure using dictionary learning. Their robustness depends on the richness of the dictionary, but, contrary to analytical approaches with highly non linear equations, MC approaches do not have limitation, enabling to simulate/decode more complex configurations, and to extent it to gray matter. Future work will consist of integrating more complex geometries (angular dispersion, bundle crossings, permeability) and to benchmark the approach with respect to analytical approaches.

Acknowledgements

This work was partially funded by the European FET Flagship ‘Human Brain Project’ (SP2) FP7-ICT-2013-FET-F/604102

References

1. ALEXANDER, Daniel C. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue-microstructure features. Magnetic Resonance in Medicine, 2008, vol. 60, no 2, p. 439-448.

2. ASSAF, Yaniv, BLUMENFELD-KATZIR, Tamar, YOVEL, Yossi, et al. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magnetic Resonance in Medicine, 2008, vol. 59, no 6, p. 1347-1354.

3. ZHANG, Hui, SCHNEIDER, Torben, WHEELER-KINGSHOTT, Claudia A., et al. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 2012, vol. 61, no 4, p. 1000-1016.

4. DE SANTIS, Silvia, JONES, Derek K., et ROEBROECK, Alard. Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage, 2016, vol. 130, p. 91-103.

5. COOK, P. A., BAI, Y., NEDJATI-GILANI, S. K. K. S., et al. Camino: open-source diffusion-MRI reconstruction and processing. In : 14th scientific meeting of the international society for magnetic resonance in medicine. Seattle WA, USA, 2006.

6. YEH, Chun-Hung, SCHMITT, Benoît, LE BIHAN, Denis, et al. Diffusion microscopist simulator: a general Monte Carlo simulation system for diffusion magnetic resonance imaging. PloS one, 2013, vol. 8, no 10, p. e76626.

7. CHANG, Chih-Chung et LIN, Chih-Jen. LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, vol. 2, no 3, p. 27.

8. ABOITIZ, Francisco, SCHEIBEL, Arnold B., FISHER, Robin S., et al. Fiber composition of the human corpus callosum. Brain research, 1992, vol. 598, no 1, p. 143-153.


Figures

Fig.1 : Specific geometry corresponding to axon diameter of 8µm and to a spacing of 7µm (in gray) as well as the trajectories (in blue) followed by some of the 200 000 random walkers (in red) simulated using the DMS toolbox. Parameters for MC simulations : 200 000 random walkers, temporal resolution of 10µm, free diffusivity of 0.002µm²/µs at 20°C, elastic bounce model, membrane permeability null. Each geometry lies in a bounding box of size 460x460x460µm. The diameters and spacings for the 63 geometries are presented in a table.

Fig.2 : True domain of available (δ,∆,G) configurations that respects the constraints for the preclinical 11.T Bruker MRI system hardware (maximum gradient magnitude of 780mT/m, slewrate of 9600T/m/s), the target millimeter resolution (1mm : imposed gradient and RF pulses times), the b-value (100 <= b <= 10 000 s/mm²), G (Geffective <= 0,7 * Gmax = 532 mT/m to preserve the maximum duty cycle) and TE (<= 60 ms to preserve the SNR). In total, there are 343 settings of (δ,∆,G) (4 possible TEs, 10 different δ, 4 different ∆, 25 different G).

Fig.3 : Overview of the dictionary matrix of fractional anisotropy (FA) and mean (ADC), perpendicular (λtransverse) and longitudinal (λparallel) diffusivities stemming from the diffusion tensor for one simulation on the 63 geometries, showing how these parameters vary according to the diffusion sensitization setting and to the geometry, assessing the feasibility to distinguish the geometry using such information with a supervised classifier. The global matrix is composed of 63000 lines and 1372 columns (for the 63 geometries x 1000 simulations/geometry and for the 343 PGSE settings x [ADC, FA, λparallel, λtransverse]).

Fig.4 : Designed synthetic corpus callosum from the diagram presented by Aboitiz8 illustrating the spatial distribution of fibers according to their diameter in a cross-section of the human corps-callosum (the color indicates the chosen geometry among the 63 simulated ones). Axon diameters vary from 1 µm in general in the genu/splenium, to 3-7 µm in the body according to histological studies8.

Fig.5 : Axon diameter mapping obtained on the synthetic corpus callosum using different levels of signal to noise. We can observe that there is 100% of success for the standard noise level of the preclinical 11.T Bruker MRI system hardware and for noise level 1.5. When using higher noise level (2 and above) the tool fails to decode diameters below 4µm like ActiveAx, even if the ratio between diameter and spacing is preserved.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3380