3375
Evaluating NODDI’s a priori fixed parameters by combining NODDI and mcDESPOT1Clinical Imaging Sciences Centre, Brighton and Sussex Medical School, Brighton, United Kingdom, 2Neuroimaging, IoPPN, King’s College London, London, United Kingdom, 3Wellcome Trust Consortium for Neuroimmunology of Mood Disorders and Alzheimer’s Disease, London, United Kingdom, 4Centre for Medical Image Computing, University College London, London
Synopsis
NODDI is a popular diffusion MRI technique that estimates indices about tissue microstructure. However it makes a priori assumptions, particularly fixing intrinsic diffusivity (DI) to be the same throughout the brain. We aim to validate this assumption by combining NODDI with mcDESPOT, which enables an independent estimation of the CSF volume fraction. By doing this, we enable NODDI to estimate voxel-wise maps of DI as well as of the perpendicular diffusivity by removing the tortuosity constraint. Our estimated DI maps show that the assumed value is more suitable for white matter than gray matter and resulted in sharper contrast in neurite density maps but noisier orientation dispersion (ODI) maps. Removing the tortuosity assumption restored the ODI but degraded the quality of the neurite density map.
Aim
Validate some of NODDI's a priori assumptions, such as the intrinsic diffusivity value, by combining it with mcDESPOT, which enables an independent estimation of the CSF volume fraction.Introduction
Neurite orientation dispersion and density imaging (NODDI 1) is a popular diffusion MRI technique that estimates indices about tissue microstructure. However, NODDI makes a priori assumptions, particularly fixing intrinsic diffusivity (DI) to $$$1.7 \star 10^{-9} m^2.s^{-1}$$$. Guerrero et al. in 2 experimented with a range of values for fixed DI to find the optimum value that provided best fitting and the effect it has on NODDI’s indices. We aim to evaluate NODDI’s assumption and aid NODDI to estimate DI using a voxel-wise approach by combining NODDI and Multi-component driven equilibrium single pulse observation (McDESPOT 3), a multi-component relaxation analysis technique. McDESPOT estimates volume fractions of CSF, myelin and intra/extra-cellular (IE) space as well as T1 and T2 maps. Supplying an independent estimate of the CSF volume fraction enables additional parameters, previously fixed, to be estimated directly by the NODDI fitting. In this proof of concept study, we attempt to estimate DI, as well as the perpendicular diffusivity.Methods
NODDI and mcDESPOT images were acquired for 3 healthy subjects (2 male and 1 female, median age 38, range 27-44 years) using a Siemens Prisma 3T scanner (maximum gradient strength=80mT/m). NODDI data were acquired using TE/TR=95/8200ms, FoV=240x240mm2, matrix size 96x96, slices=60, thickness=2.5mm. Two diffusion shells were used, b=800 and 2000s/mm2 with 30 and 60 non-collinear directions, respectively. McDESPOT data acquisition protocol included 8 T1-weighted SPGR images and 16 balanced T1/T2-weighted bSSFP images acquired using multiple flip angles, as described in3. We performed mcDESPOT 3-pool fitting to generate volume fractions of CSF (fCSF).
For each subject, NODDI and mcDESPOT data were
co-registered using SPM12. Then we carried out NODDI fitting on the diffusion
data using the NODDI toolbox. We experimented with various options of NODDI
fitting as shown in Table 1. It is worth noting that when NODDI's CSF volume
fractions (fiso) are fixed to mcDESPOT'S fCSF estimates, the latter is weighted
by relative T2 values. This is necessary since
NODDI’s estimates are relaxation weighted 4.
Results and discussion
Figure 1 shows the resulting voxel-wise map of the intrinsic diffusivity as estimated by NODDI using fitting option 3 as described in table 1. There is a significant contrast between gray and white matter, with the estimated intrinsic diffusivity values ranging between $$$0.7-1.2 \star 10^{-9} m^2.s^{-1}$$$ for the gray matter and between $$$1.5-2.2\star 10^{-9} m^2.s^{-1}$$$ for the white matter. We can observe that while the assumed fixed intrinsic diffusivity for all voxels $$$1.7 \star 10^{-9} m^2.s^{-1}$$$ is acceptable for the white matter regions, it might not be suitable for gray matter regions.
Figure 2 shows the estimated intrinsic diffusivity map and perpendicular diffusivity map calculated by NODDI using fitting option 4. The NODDI fitting in this scenario is carried out without the tortuosity assumption. It is worth noting that when the tortuosity assumption is removed, the DI is no longer so contrasted between white and gray matter, and the values are close to the assumed value of $$$1.7 \star 10^{-9} m^2.s^{-1}$$$.
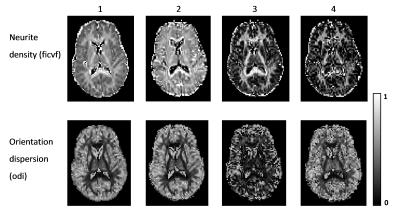
The other NODDI indices, neurite density (ficvf) and orientation dispersion (odi), estimated in all 4 fitting options are presented in figure 3. Allowing NODDI to fit for the intrinsic diffusivity results in sharper contrast between the estimated neurite density of white and gray matter. ODI is decreased, particularly in gray matter, and the map appears significantly noisier than those obtained with options 1 and 2.
Removing the tortuosity assumption mitigates some of the effects of freeing the perpendicular diffusivity with the ODI being restored; however, the quality of the neurite density map is degraded.
Conclusion
We showed that by using mcDESPOT's CSF volume fractions, we can allow NODDI to carry out further parameter fitting, and estimate voxel-wise intrinsic diffusivity (DI) maps. The calculated DI maps showed that the assumed fixed value in the original NODDI toolbox is more suitable for white matter than gray matter regions. We showed the effect these newly estimated maps have on other NODDI indices such as neurite density and orientation dispersion. Additionally, we showed the effect of removing the tortuosity assumption from the model to estimate both intrinsic and perpendicular diffusivities on NODDI indices.Acknowledgements
This work was supported by the Wellcome Trust Neuroimmunology Consortium (NIMA).
Thanks to Samuel Hurley for providing us with the mcDESPOT sequence.
References
1. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 2012; 61:1000-1016.
2. Guerrero JM, Adluru N, Kecskemeti SR, Davidson RJ, Alenxander AL. Investigating the effects of intrinsic diffusivity on neurite orientation dispersion and density imaging (NODDI). ISMRM 2016.
3. Deoni SC, Matthews L, Kolind SH. One component? Two components? Three? The effect of including a nonexchanging "free" water component in multicomponent driven equilibrium single pulse observation of T1 and T2. Magnetic Resonance in Medicine 2013; 70:147-154.
4. Bouyagoub S, Dowell NG, Hurley S, Wood TC, Cercignani M. Overestimation of CSF fraction in NODDI: possible correction techniques and the effect on neurite density and orientation dispersion measures. ISMRM 2016.
Figures
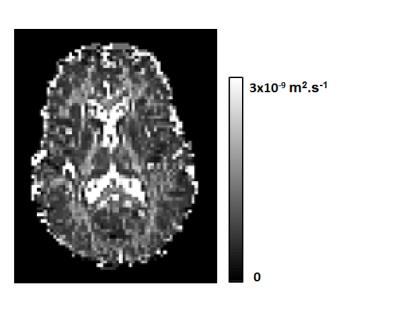
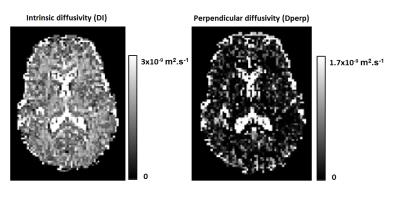
Figure 2: Intrinsic diffusivity (DI) and perpendicular diffusivity (Dperp) estimated by NODDI in scenario 4(see methods), after fixing CSF volume fractions to those estimated by mcDESPOT, and dropping the tortuosity assumption from the NODDI model.