3373
Density-Based Non-Rigid Registration of Diffusion-Weighted Images1Computer Science, University of Copenhagen, Copenhagen, Denmark
Synopsis
We present a non-rigid registration method for Diffusion-Weighted MRI which uses a density and scale space approach to estimate image similarity. It allows us to employ smooth intensity-invariant similarity measures, such as Mutual Information (MI), in contrast to the model-driven registrations. Using the inherent microstructure of High Angular Resolution Diffusion Imaging (HARDI) scans, we obtain a less regularized and more flexible registration that can be used on either raw diffusion signals or reconstructions of the fiber orientations. We show some promising results on Human Connectome Project (HCP) subjects and an artificial example.
Purpose
We present a non-rigid registration approach which uses the apparent diffusion coefficient (ADC) directly, based on Locally Orderless Registration for DWI1. While model-driven registration methods (such as the ones using Spherical Deconvolution, Spherical Harmonics, or similar) reduce noise or offers smoother solutions by modelling signal frequencies and selecting peaks, they tend to be sensitive to scaling and multi-scanner variance. It is desirable to use information theoretical measures of the observations in DWI data due to their invariance properties. With a scale space approach to density estimation we are able to register diffusion data directly using the ADC between subjects. Our framework allows us to use similarity measures like Mutual Information (MI), previously reserved for registration of scalar-valued images. We illustrate the approach on a subject from the HCP and on artificial fiber-crossings.Methods
We use a non-rigid registration based on B-splines, and the density estimation scheme described by Jensen et al2, to estimate the joint and marginal distributions over intensity, location, and orientation. The histogram is estimated as
$$h_{\beta\alpha\sigma\kappa}(i,j|\vec x)=\int_{\Omega\times S^2}P_\beta(I_{\sigma\kappa}(\vec x,\vec v)-i)P_\beta(J_{\sigma\kappa}(\vec x,\vec v)-j)d\vec x\times d\vec v$$
where
$$I_{\sigma\kappa}(\vec x,\vec v)=\int_{S^2} \left( \int_\Omega I(\vec \tau,\vec \nu)K_\sigma(\vec \tau-\vec x)d\vec \tau\right) \Gamma_{\kappa}(\vec \nu, \vec v) d\vec \nu=(I*(K_{\sigma}\otimes \Gamma_{\kappa}))(\vec x,\vec v)$$
and $$$\sigma$$$ is the image scale, $$$\kappa$$$ is the orientation scale, and $$$\beta$$$ is the intensity scale. $$$P$$$, $$$K$$$, and $$$\Gamma$$$ are kernels in intensity, location, and orientation respectively. In our experiments, the location scale is modelled by B-splines and the orientation scale by a bidirectional Watson kernel. The histogram is normalised to generate a density estimate from which MI, normalized MI, and other density-based image similarity measures can be estimated.
Results
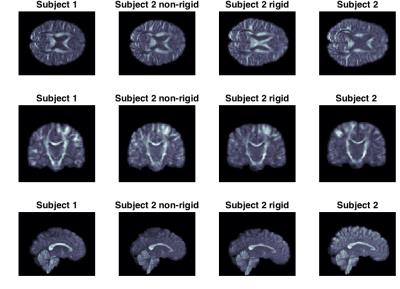
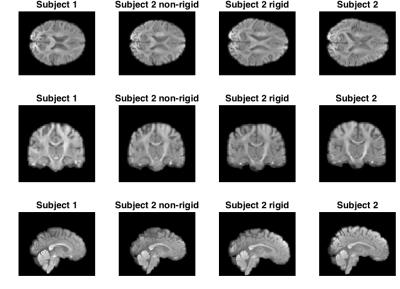
We selected a full brain DWI of a single HARDI shell from two randomly chosen subjects from the HCP. We used scans with a b-value of 3000. The resolution is 1mm isotropic voxel with 90 directions. In Figure 1 and 2, the subject is first aligned by a global rigid transformation and then aligned by the non-rigid registration.
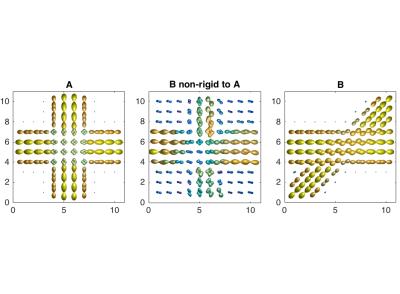
We also constructed two artificial DWI samples containing fiber ODFs, one that simulates a fiber-crossing with a 90 degree angle and one that simulates a 45 degree angle crossing. The resolution is set to 1mm isotropic voxels with 90 directions. Figure 3 illustrates the transformation of the 45 degree crossing to the 90 degree crossing.
Discussion
As the results show, the method is able to align both the real images and the artificial example.
Although unlikely to occur in real data, the artificial example illustrates the ability of the method to capture the transformation under such extreme cases. A direct map between the two crossings is not to be expected given the large local deformation needed, but we see that our model generalises well. Smoothing effects on the isotropic ODFs are to be expected and can be observed in the corners of the transformation.
Our experiments on real data show that the transformation, and the estimated non-rigid deformation, provides an excellent fit between the interpolation of subject 1 and the transformed subject 2 (this also generalises to other gradient directions). The application of the registration using B-splines shows that a very good apparent alignment can be achieved.
It is worth mentioning that the use of a Watson distribution $$$\Gamma$$$ allows us to register fiber orientations by using negative $$$\kappa$$$. However, it appears that no real difference is observed between positive and negative $$$\kappa$$$.
We believe in taking advantage of the full recorded signal (the whole of the DWI signal) including noisy observation to estimate the transformation in contrast to using the dominant features derived from the signal. The latter may in some cases oversimplify the signal which potentially could lead to additional overfitting.
It is our belief that in the context of registration, computations on deformed DWI data (such as tractography or modelling of fibers) should be avoided as the deformed data in no way represents any anatomy, but merely serves the purpose of estimating a transformation between any two subjects. Computation should be performed in the native space. However, for illustration purposes we have transformed the ODFs according to the deformation to show the optimum found using the similarity measure.
Conclusion
We have presented a non-rigid registration similarity measure which directly relies upon the ADC and allows us to register diffusion scans rather than a fiber-model. As the results show, we are able to effectively perform inter-subject registration. Furthermore, we are able to match regions with potential large anatomical variability as the artificial example shows.Acknowledgements
Data were provided [in part] by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.References
[1] Jensen, Henrik G., et al. "Locally Orderless Registration for Diffusion Weighted Images." International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer International Publishing, 2015.
[2] David C. Van Essen, Stephen M. Smith, Deanna M. Barch, Timothy E.J. Behrens, Essa Yacoub, Kamil Ugurbil, for the WU-Minn HCP Consortium. (2013). The WU-Minn Human Connectome Project: An overview. NeuroImage 80(2013):62-79.
Figures