3368

A New Fiber Orientation Distribution Function
Tom Dela Haije1, Andrea Fuster1, and Luc Florack1

1Department of Mathematics and Computer Science, Eindhoven University of Technology, Eindhoven, Netherlands

Synopsis

In this work we introduce the barrier orientation distribution function (ODF) as an alternative to the fiber ODF that can be computed with constrained spherical deconvolution. The barrier ODF is computed directly from the data, without the need to e.g. specify a single fiber response function.

Purpose

At this time there are two widely accepted approaches to extract the orientations of fibers from diffusion MRI data. The first consists of radially integrating the ensemble average propagator, which can be done for a large variety of signal models, leading to the so-called diffusion orientation distribution function1 (ODF). This distribution provides a limited answer to the question of orientation: its local maxima have been shown to correspond well to the dominant tissue orientations, but it does not provide a distribution describing the fiber orientations. The second approach, based on spherical deconvolution, does produce such a fiber ODF, by determining to what extent the signal along each orientation resembles a single fiber response function2. The downside is, that it is unclear if and how it is possible to properly define an appropriate response function. In this abstract we propose a new kind of ODF that does not require a response function, based on the assumption that fibers in a macroscopically uniform medium can be modeled as barriers that slow down diffusing particles, as considered by e.g. Novikov et al.3

Theory

Let us for the purpose of this discussion assume that all impedance endured by diffusing particles is the result of the presence of fiber-like barriers as visualized in Fig. 1: no barriers means movement is unrestricted, and the density of barriers encountered has a linear effect on the impedance. Though we will assume that these barriers can model fibers and other tissue constituents, note that there is a distinction. Diffusing particles are subject to a baseline impedance, whose effect we do not separate from the impedance caused by e.g. axons. Hence a freely diffusing particle should be understood as encountering isotropically distributed barriers.

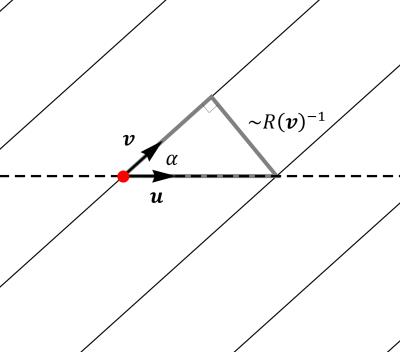
Let now $$$R$$$ denote the probability density function describing the distribution of linear barriers, and assume that $$$R$$$ is voxel-wise homogeneous (i.e., approximately independent of position within a voxel). $$$R(\textbf{v})\,d\textbf{v}=R(\textbf{-v})\,d\textbf{v}$$$ gives the likelihood that any barrier within the voxel is locally tangent to an orientation $$$\textbf{v}\in S^2$$$, and $$$R$$$ is normalized so that $$$\int_{S^2}\!R(\textbf{v})\,d\textbf{v}=1$$$. Compared to the maximum, the fraction of barriers with local orientation $$$\textbf{v}$$$ that cross a unit vector $$$\textbf{u}$$$ is easily shown to be (on average) the sine of the angle $$$\alpha$$$ between $$$\textbf{u}$$$ and $$$\textbf{v}$$$, Fig. 2. This means that the total fraction of the maximum number of barriers that can be crossed by $$$\textbf{u}$$$ is given by $$\mathcal{S}\{R\}(\textbf{u}):=\int_{S^2}\!\sqrt{1-|\textbf{u}\cdot\textbf{v}|^2}\,R(\textbf{v})\,d\textbf{v},$$ the sine transform of $$$R$$$. If we assume that this barrier density is inversely proportional to the maximum possible particle displacement $$$\partial\Omega(\textbf{u})$$$ along $$$\textbf{u}$$$ then it follows that $$$\partial\Omega(\textbf{u})\mathcal{S}\{R\}(\textbf{u})$$$ is constant, where $$$\partial\Omega(\textbf{u}):=\sup_{\lambda\in\mathbb{R}}\{\lambda\,|\,\lambda\,\textbf{u}\in\Omega\}$$$ is the boundary of the domain $$$\Omega$$$ of the ensemble average propagator. The boundary $$$\partial\Omega$$$ can be approximated by high gradient strength diffusion MRI4, as follows from the Fourier-Laplace relation between the normalized pulsed-gradient spin echo signal $$$E$$$ and the propagator in the limit $$$\|\textbf{q}\|\to\infty$$$ (following the convention $$$\textbf{q}:=\gamma\delta\textbf{G}$$$): $$\log{E(-i\textbf{q})}\sim\sup_{\textbf{r}\in\partial\Omega}\textbf{q}\cdot\textbf{r}=:H(\textbf{q})\hspace{2em}(\|\textbf{q}\|\to\infty).$$ Here we implicitly assume that the propagator has an associated moment-generating function, so that its extension to complex-valued arguments is well-defined. $$$H$$$ is recovered from a level set of the cumulant-generating function (CGF) $$$\log{E(-i\textbf{q})}$$$, and is related to $$$\partial\Omega$$$ through the duality relation5, Chapter 14 $$$H(\textbf{q})=\sup_{H^*(\textbf{r})=1}\textbf{q}\cdot\textbf{r}$$$, where the dual $$$H^*$$$ is the unique homogeneous function for which $$$\partial\Omega=\{\textbf{u}\,|\,H^*(\textbf{u})=1\}$$$. By linearity we then find the barrier ODF (bODF) $$R(\textbf{v})\propto\mathcal{S}^{-1}\{H^*\}(\textbf{v}).$$

Methods and Results

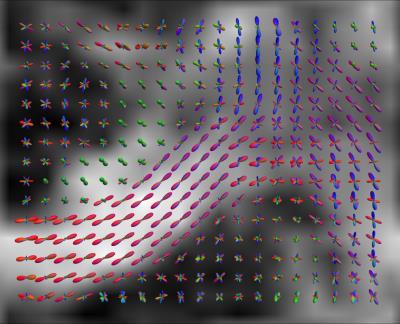
As an initial validation, we implemented the analytical inversion of $$$\mathcal{S}$$$ by expressing level sets of (constrained6) reconstructed CGF (including up to order four cumulants) in terms of spherical harmonics and applying the Funk-Hecke theorem7. The algebraic dual is approximated numerically using the equality5 $$H(\textbf{q})=H^*\left(\left(\frac{1}{2}\nabla^2H^2(\textbf{q})\right)\cdot\textbf{q}\right).$$ We apply this to a human connectome project data set8 ($$$b=1000\,s/mm^2$$$ and $$$b=2000\,s/mm^2$$$ shells only), giving the bODF map shown in Fig. 3. Results are comparable to those of constrained spherical deconvolution (CSD, based on the $$$b=3000\,s/mm^2$$$ shell and computed with MRtrix39, default settings) shown in Fig. 4. Peaks derived from these maps are shown in Fig. 5.

Discussion and Conclusion

We defined a new ODF called the barrier ODF or bODF, which is capable of at least qualitatively reproducing local fiber orientation distributions as computable from CSD, without the need of a fiber response function. Preliminary results show that the barrier ODF is typically less sharp than the fiber ODF, but also seems to suffer from fewer spurious peaks. We do note that the current comparison is not definitive, as the ODFs in the presented experiments are based on data from different shells. A more complete comparison between the barrier ODF and other ODFs is subject of future work.

Acknowledgements

The authors gratefully acknowledge the Netherlands Organization for Scientific Research (NWO, No. 617.001.202) for financial support, and the work of Andrea Fuster is part of the research programme of the Foundation for Fundamental Research on Matter (FOM), which is financially supported by NWO. Joep Kamps is acknowledged for his help in setting up the constrained reconstruction, and Jorg Portegies is acknowledged for running the MRtrix experiment. Data were provided in part by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.

References

[1] Tuch. MRM 52, no. 6 (2004): 1358–72.
[2] Tournier et al. NeuroImage 23, no. 3 (2004): 1176–85.
[3] Novikov et al. PNAS 111, no. 14 (2014): 5088–5093.
[4] Dela Haije et al., in Proc. Intl. Soc. Mag. Reson. Med. 24 (2016): p. 2084.
[5] Bao et al. An Introduction to Riemann-Finsler Geometry. Springer, 2000.
[6] Dela Haije et al., in Proc. Intl. Soc. Mag. Reson. Med. 23 (2015): p. 2821.
[7] Descoteaux et al. MRM 58, no. 3 (2007): 497–510.
[8] Van Essen et al. NeuroImage, no. 80 (2013): 62–79.
[9] Tournier et al. NeuroImage, no. 35 (2007): 1459-1472.

Figures

An illustration of fiber-like linear barriers, with isotropically distributed local orientations within a voxel (black box), used to model fibers and other tissue constituents. Barriers are assumed to have an additive impeding effect on diffusion; particles that encounter twice the number of barriers can only travel half the distance they could otherwise. We assume that the local orientations (tangents) of these barriers within a voxel can be modeled as if randomly drawn from a probability density function $$$R$$$.

The relative maximum distance particles can travel along $$$\textbf{u}$$$ (dashed line) is determined by the density of barriers they encounter (illustrated with the black parallel lines, shown only for $$$\textbf{v}$$$). This density is inversely related to the expected distance between barriers, which is given by the sine of the angle $$$\alpha$$$ between $$$\textbf{u}$$$ and the barrier orientation $$$\textbf{v}$$$.

The barrier ODF in a segment of a coronal slice showing the corpus callosum entering the centrum semiovale.

Fiber ODFs in the same region as in Fig. 3, computed with constrained spherical deconvolution.

Peaks computed from the ODFs shown in Fig. 3 (barrier ODF, on the left) and Fig. 4 (fiber ODF, on the right). Only peaks larger than $$$70\%$$$ of the voxel-wise maximum ODF value are displayed.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3368