Synopsis

We compute the higher-order statistics of the 3D spin displacement probability distributions measured with mean apparent propagator (MAP) MRI and quantify microstructural tissue parameters such as the mean kurtosis (MK), axial kurtosis (K_∥), radial kurtosis (K_⊥) and kurtosis fractional anisotropy (FA_K). This extension of the family of MAP tissue parameters provides a direct link between the frameworks of MAP MRI and other advanced diffusion techniques facilitating interpretation of findings in clinical MAP MRI studies in the context of existing literature on advanced diffusion MRI applications.

Purpose

We derive analytical expressions for computing the higher-order statistics of 3D probability distributions of spin displacements (i.e., diffusion propagators) measured with mean apparent propagator (MAP) MRI¹, and for quantifying microstructural tissue parameters² conventionally derived with methods that rely on the cumulant expansion of the MR signal phase, such as generalized diffusion tensor imaging (GDTI)^3,4, and, in particular, diffusional kurtosis imaging (DKI)⁵. This extension of MAP MRI provides the ability to make a direct quantitative comparison of MAP-derived parameters and parameters obtained from other diffusion methods, and to compare and harmonize findings in the scientific and clinical diffusion MRI literature.

Purpose

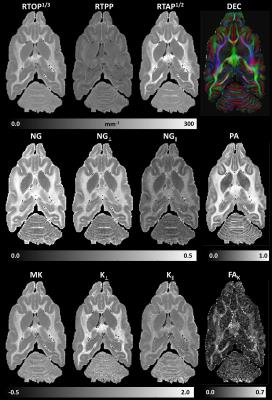
We acquired high-quality diffusion MRI dataset (250x250x250µm³, TE/TR=36/700ms) in fixed ferret brain with diffusion gradients applied along orientations uniformly sampled on the unit sphere at five b-values (b_max=13500s/mm²). We measured the diffusion propagators using MAP MRI (up to order 6) and derived microstructural parameter maps of return-to-origin, -axis, and -plane probabilities (RTOP, RTAP, RTPP); total, axial, and radial non-gaussianity (NG, NG_∥, NG_⊥); and propagator anisotropy (PA).

From the 3D diffusion propagators measured in the MAP MRI functional basis $$$\Psi_{m_{1}m_{2}m_{3}}(\bf{u},\bf{r})$$$ (up to order $$$M_{max}=6$$$) defined by scaling vector u¹: $$P({\bf{r}})=\sum_{M=0}^{M_{max}}\sum_{m_{1}+m_{2}+m_{3}=M}^{}a_{m_{1}m_{2}m_{3}}\Psi_{m_{1}m_{2}m_{3}}(\bf{u},\bf{r})$$ we quantify the higher-order statistical moment tensors of order N $$${\bf{\mu_{N}}}=\mu_{n_{1}}\mu_{n_{2}}\mu_{n_{3}}=\int_{-\infty}^{\infty}P({\bf{r}})x^{n_{1}}y^{n_{2}}z^{n_{3}}d{\bf{r}}$$$ (denoted here using the so-called “occupation number” notation⁶) both numerically, by integrating $$$P({\bf{r}})$$$, and analytically, by using a series of linear transformations $$\bf{\mu_{N}=aY_{N}U_{N}}$$, where $$${\bf{a}}=a_{m_{1}m_{2}m_{3}}$$$ is the row vector of MAP MRI coefficients that describes $$$P({\bf{r}})$$$, $$${\bf{Y_{N}}}=Y_{m_{1}n_{1}}Y_{m_{2}n_{2}}Y_{m_{3}n_{3}}$$$ is a constant matrix with $$Y_{mn}=K_{m+n}\sqrt{m!}\sum_{r=0,2,...}^m\frac{(-1)^{\frac{r}{2}}2^{m-r}}{r!!(m-r)!}\Gamma(\frac{m+n-r+1}{2})$$, $$$K_{m+n}=1$$$ if m and n are even, and 0 otherwise, $$$\Gamma(x)$$$ is the Gamma function, and $$${\bf{U_{N}}}=u_x^{n_{1}}u_y^{n_{2}}u_z^{n_{3}}\sqrt{\frac{2^{N}}{\pi^{3}}}$$$ is a diagonal scaling matrix. From $$$\bf{\mu_{N}}$$$ we compute the cumulant tensors⁷ and higher-order diffusion tensors (HOTs) as described in³, along with parameters such as mean kurtosis (MK), axial kurtosis (K_∥), radial kurtosis (K_⊥) and kurtosis fractional anisotropy (FA_K)^2,5,8.

In addition, we directly analyze the DWI data with GDTI (order 6) by first re-orienting the q-vectors in the DTI reference frame (which is the same as in MAP MRI) before fitting the data^1,9. We measure the kurtosis tensors⁵ along with the DKI parameters MK, K_∥, K_⊥, and FA_K, to compare with the MAP-derived quantities.

Results

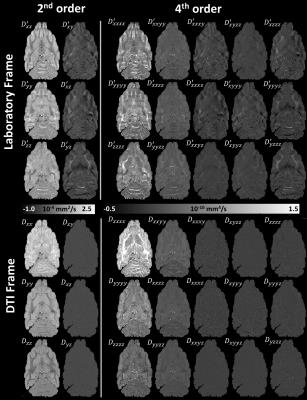
The moment tensors of MAP propagators derived analytically (Eq.2) were verified by numerical integration. Fig.1 shows how GDTI (or DKI) analysis can be performed directly in the DTI reference frame (just like MAP MRI¹) by re-orienting the q-vectors (or b-matrices respectively) before fitting the data^1,9, without affecting the measurement of rotation-invariant parameters¹⁰ such as the MK, K⊥, K∥, and FA_K². Analyzing the data in the DTI reference frame⁹ “diagonalizes” the HOTs¹¹ and may provide opportunities for regularization and sparse encoding.

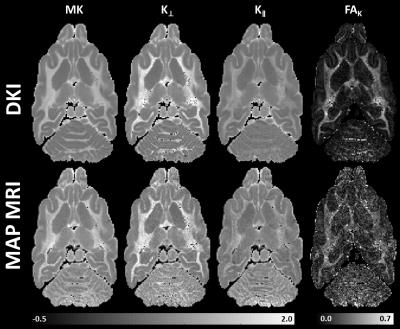
Microstructural parameters MK, K_⊥, K_∥, and FA_K derived from the higher-order statistics of MAP propagators showed good agreement with corresponding parameters derived with GDTI/DKI (Fig.2) and complement the MAP MRI microstructural assessment (Fig. 3). Differences between the parameters in Fig.2 may be attributed to truncations of MAP and GDTI series approximations.

Discussion

Computation of DKI parameters within the analytical MAP framework does not require numerical integration, and is therefore faster and more accurate than methods that measure the propagators numerically, such as diffusion spectrum imaging (DSI)¹².

Due to the limited number of DWI measurements the truncation of the MAP (or GDTI) series approximation inherently leads to inaccuracies (small oscillations) in the measured propagators for very large displacement values. While Eq.2 allows the exact computation of tensor moments (and HOTs) with arbitrarily high order form MAP propagators, in practice, very high-order statistics may amplify these spurious oscillations in the propagator approximations leading to physically inaccurate results.

Both MAP MRI and GDTI reconstruct the diffusion propagators analytically. The Gram-Charlier Series (GCS) approximates the GDTI propagator from its cumulants using Gauss-Hermite functions^3,13 similar to the MAP basis functions. However, the use of the physicists’ Hermite polynomials in MAP – compared to the statisticians’ Hermite polynomials in GCS – may allow a more robust approximation of probability distributions¹⁴ with orthogonal functions that have the desired asymptotic physical behavior¹.

Conclusions

This study serve as cross-validation of MAP MRI and diffusion methods that rely on the cumulant expansion of the MR signal phase to quantify features of the diffusion propagators. It extends the family of MAP microstructural parameters to include HOT-derived metrics, and shows that MAP MRI subsumes not only DTI but also GDTI/DKI. More importantly, it provides a direct link between the frameworks of MAP MRI and other advanced diffusion techniques facilitating interpretation of findings in clinical MAP MRI¹⁵ studies in the context of existing literature on advanced diffusion MRI applications.

Acknowledgements

References

1 Özarslan, E. et al. Mean apparent propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure. Neuroimage 78, 16-32 (2013).

2 Hui, E. S., Cheung, M. M., Qi, L. Q. & Wu, E. X. Towards better MR characterization of neural tissues using directional diffusion kurtosis analysis. Neuroimage 42, 122-134, (2008).

3 Liu, C., Bammer, R. & Moseley, M. E. Generalized Diffusion Tensor Imaging (GDTI): A Method for Characterizing and Imaging Diffusion Anisotropy Caused by Non-Gaussian Diffusion. Israel Journal of Chemistry 43, 145-154 (2003).

4 Ozarslan, E. & Mareci, T. H. Generalized diffusion tensor imaging and analytical relationships between diffusion tensor imaging and high angular resolution diffusion imaging. Magn Reson Med 50, 955-965 (2003).

5 Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H. Z. & Kaczynski, K. Diffusional kurtosis imaging: The quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 53, 1432-1440 (2005).

6 Eggers, H. & Lipa, P. HBT shape analysis with q-cumulants. Brazilian Journal of Physics 37, 877-884 (2007).

7 McCullagh, P. Tensor Notation and Cumulants of Polynomials. Biometrika 71, 461-476 (1984).

8 Jensen, J. H. & Helpern, J. A. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed 23, 698-710 (2010).

9 Basser, P. J., Mattiello, J. & LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophys J 66, 259-267 (1994).

10 Qi, L. Q., Wang, Y. J. & Wu, E. X. D-eigenvalues of diffusion kurtosis tensors. J Comput Appl Math 221, 150-157 (2008).

11 Comon, P. in 10th IFAC Symposium on System Identification (IFAC-SYSID). 77-82 (IEEE).

12 Wedeen, V. J., Hagmann, P., Tseng, W.-Y. I., Reese, T. G. & Weisskoff, R. M. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 54, 1377-1386 (2005).

13 Liu, C., Bammer, R., Acar, B. & Moseley, M. E. Characterizing non-gaussian diffusion by using generalized diffusion tensors. Magn Reson Med 51, 924-937 (2004).

14 Wellig, M. Robust series expansions for probability density estimation. (California Institute of Technology, Computer Vision Lab, 1999).

15 Avram, A. V. et al. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. Neuroimage 127, 422-434 (2016).