3362

Investigating microstructural signatures for low-grade gliomas using Linear Multi-scale Modeling of diffusion MRI data
Barbara D. Wichtmann1,2, Aapo Nummenmaa1, Qiuyun Fan1, Thomas Witzel1, Elizabeth R. Gerstner3, Alexandra J. Golby4,5, Sandro Santagata6, Bruce R. Rosen1, Lothar Schad2, Lawrence L. Wald1,7, and Susie Y. Huang1,7

1A. A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Harvard Medical School, Charlestown, MA, United States, 2Computer Assisted Clinical Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany, 3Department of Neurology, Center for Neuro-Oncology, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 4Department of Neurosurgery, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 5Department of Radiology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 6Department of Pathology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 7Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States

Synopsis

Linear Multi-scale Modeling (LMM) of diffusion MRI data is a recently developed DWI analysis technique for separating orientation distributions of restricted and hindered diffusion water compartments over a range of length scales, thereby allowing more detailed characterization of tissue microstructure. Here, we apply the LMM framework to characterize a low-grade oligodendroglioma prior to resection. We use the distinct microstructural signature of the tumor to delineate tumor extent and use results from pathology and numerical simulations to refine our understanding of the tumor microstructure.

Purpose

Delineating the extent of infiltrative brain tumors by MRI is important for treatment planning and response assessment but remains a diagnostic challenge, as the extent of T2/FLAIR abnormality on conventional MRI does not correlate well with true tumor extent[1]. Diffusion MRI offers a more specific probe of local tissue architecture and structure for quantifying and mapping the histologic features of tumors in vivo[2]. Linear Multi-scale Modeling (LMM) [3] is a recently developed analysis framework for diffusion MRI data that estimates tissue microstructure parameters, including volume fractions of restricted and hindered water over a range of length scales and orientation distribution information. LMM has shown promise for identifying distinct diffusion microstructural signatures of pathology compared to healthy tissue. In this work, we apply the LMM framework to characterize a low-grade oligodendroglioma prior to resection. We use the distinct microstructural signature of the tumor to delineate tumor extent and use results from pathology and numerical simulations to refine our understanding of the tumor microenvironment.

Methods

Data acquisition. With approval from the institutional review board, a pre-surgical patient with a left frontal oligodendroglioma (WHO grade II) was scanned on a dedicated high-gradient 3T MRI scanner (MAGNETOM CONNECTOM, Siemens Healthcare) with a maximum gradient strength of 300mT/m using a custom-made 64-channel head coil [4]. Sagittal 2-mm isotropic resolution diffusion-weighted spin echo EPI images were acquired using simultaneous multislice(SMS) [5] imaging and zoomed/parallel imaging [6] for high-resolution whole-brain coverage. The following parameters were used: δ/Δ=8/19,8/49ms, 4-5diffusion gradient increments linearly spaced from 55-293mT/m per Δ, TE/TR=77/3600ms, GRAPPA acceleration factor R=2, and SMS MB factor=2. Diffusion gradients were applied in 32/64/128non-collinear directions with interspersed b=0 images every 16 directions. The maximum b-value at Δ was 10,000s/mm2. Sagittal T1-MPRAGE and T2-SPACE-FLAIR images were also acquired. Total acquisition time was approximately 60min. Following resection, the tumor was processed with standard pathology and H&E staining.

LMM analysis. Following preprocessing to correct for gradient nonlinearity, motion and eddy currents[7], spherical harmonics expansion of order 6/8 with Laplace-Beltrami regularization[8] (λ=0.006) was used to interpolate the diffusion signal on each q-shell. To obtain the orientation distribution and corresponding volume fraction estimates, the linear multi-scale deconvolution inverse problem, as described in Fig.1, was solved by standard least-squares estimation with Tikhonov regularization. Profiles of restricted, hindered and free volume fractions for normal white, gray matter were derived by averaging volume fraction estimates over all white and cortical gray matter voxels in the normal right hemisphere(Freesurfer-segmentation). The tumor region was segmented manually by an experienced neuroradiologist using T1/T2 anatomic images. A microstructural signature specific for tumor was defined by calculating the difference between pathologic white/gray matter voxels within the tumor and normal white/gray matter profiles. Using the derived profiles as predictors, voxel wise linear least-squares regression was performed in order to decompose the estimated volume fractions into a white, gray matter and tumor component (Fig.4).

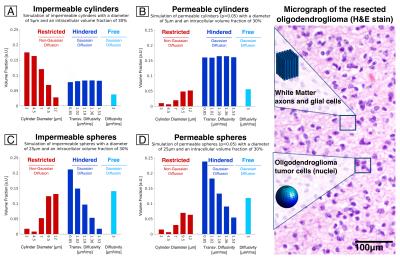
Simulation. To understand the biophysical basis underlying the estimated volume fraction profiles, synthetic MRI data was generated using the Camino Monte Carlo diffusion simulator[9] for diffusion within permeable/impermeable cylinders and spheres of different sizes and packing densities. Simulation results were compared to the experimental LMM tumor profiles as well as to histology.

Results

The tumor region demonstrated increased hindered and free water and decreased restricted water compared to normal white and gray matter (Fig.2/3). Fig.4 illustrates the decomposition of the estimated volume fractions into white matter, gray matter and tumor components. Simulation results indicated that while increasing the compartment size and decreasing the intra-cellular volume fraction could increase the proportion of hindered water, the uniformly increased hindered water observed experimentally in the tumor was most closely captured by increasing the permeability of the cylinders (Fig.5).

Discussion

Using the LMM analysis, we developed a microstructural signature for the low-grade glioma studied in this patient, which showed uniformly increased hindered water and decreased restricted water within the tumor. We then applied this signature to improve our understanding of the tumor microenvironment. Simulation results showed that increased permeability in the cylinder model most closely emulated the volume fraction profiles in the tumor, which suggests that low-grade gliomas infiltrate and possibly alter the permeability of normal-appearing white matter. Future work will focus on validating these assumptions through systematic correlation with histology and mapping the rate of water exchange within tumors through filter exchange imaging[10].

Conclusion

The LMM analysis was used to derive a tumor-specific microstructural signature in a low-grade glioma, characterized by decreased restricted water and increased hindered water. The presence of increased permeability in normal-appearing white matter may account in part for these changes in tumor microstructure.

Acknowledgements

Research reported in this publication was supported by the National Institutes of Health under NIBIB award number P41EB015896, U01MH093765 (Human Connectome Project), R00EB015445, 1U01CA154601, K23CA169021-01, K23NS096056, and P41EB015898-12.

References

[1] Wen PY et al. J Clin Oncol. 28(11): 1963-72 (2010).

[2] Padhani AR et al. Neoplasia 11.2: 102-125 (2009).

[3] Wichtmann B et al. ISMRM 24: 5142 (2016).

[4] Keil B et al. MRM 70(1): 248-258 (2013).

[5] Setsompop K et al. NI 80:220 (2013).

[6] Eichner C et al. MRM 71: 1518-1525 (2014).

[7] Fan Q. et al. Brain Connect 4: 718-726 (2014).

[8] Descoteaux M et al. MRM 58: 497-510 (2007).

[9] Cook PA et al. ISMRM 14: 2759 (2006).

[10] Nilsson M et al. Magn Reson Med 69:1572-1580 (2013).

[11] van Gelderen P et al. Journal of magnetic resonance 103: 255-260 (1994)

[12] White NS et al. Hum. Brain Mapp. 34: 327-346 (2013).

Figures

Fig.1 LMM Methodology: The linear multi-scale forward model of different sized restricted and hindered diffusion compartments is obtained by concatenating two spectra of response functions: 1) a non-Gaussian diffusion response function [11] for water restricted inside cylindrical structures and 2) a Gaussian diffusion response function [12] for hindered water and free water diffusion. The diffusion-weighted signal equals the sum of each water compartment’s orientation distribution convoluted with its corresponding response function R. Each compartment’s orientation distribution is parameterized with spherical harmonics.

Fig. 2 Representative maps showing restricted and hindered volume fractions in a patient with a left frontal oligodendroglioma. The maps comprise volume fractions averaged over (A) all restricted length scales and (B) all hindered length scales. The tumor in the left frontal lobe shows a high fraction of hindered water and less restricted water compared to normal gray and white matter.

Fig. 3 Profiles demonstrating restricted, hindered and free diffusion volume fraction estimates, averaged over (A) all white matter voxels and (B) all cortical gray matter voxels within the normal right hemisphere. (C) and (D) depict average volume fraction estimates for white and gray matter voxels within the tumor, illustrating decreased restricted water and increased hindered and free water within the tumor.

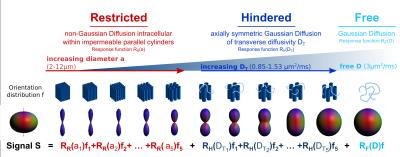
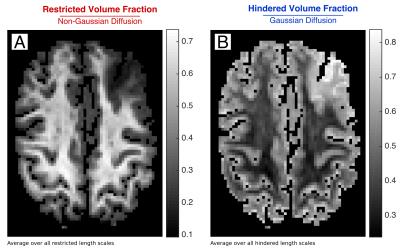
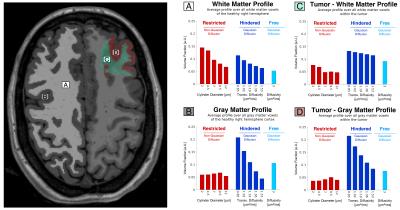
Fig. 4 Using the derived profiles for (A) white matter, (B) gray matter and (C) tumor as predictors, voxel wise constrained linear least-squares regression allows for decomposing the estimated volume fractions into a white matter, gray matter and tumor components.

The maps show linear regression coefficients for white matter, gray matter and tumor in solving the linear least-squares equation:

A · White Matter Profile + B · Gray Matter Profile + C · Tumor Profile = Volume fraction estimate in voxel, subject to A,B,C≥0.


Fig. 5 To imitate diffusion within the tumor environment, we independently simulated cylindrical and spherical compartments based on the H&E image of the resected oligodendroglioma over a range of diameters, intracellular volume fractions and different permeabilities. Especially with an increased permeability we observe a shift from restricted to hindered diffusion similarly to the tumor profile (Fig. 3(C)).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3362