3347
A new method for the image reconstruction of multi-shot navigator-free DWI1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, People's Republic of China, 2Department of Radiology, University of Washington, 1959 NE Pacific Street, SS-202, Seattle, WA 98195-7117, USA, WA, United States
Synopsis
Multi-shot techniques can help to achieve high spatial resolution in diffusion imaging. Due to the application of diffusion gradients, phase errors are induced by shot-to-shot motions, which need to be corrected during image reconstruction. Some phase correction approaches have been proposed, such as SENSE+CG, POCS-ICE, and PR-SENSE. Compressed sensing (CS) method has been used in image reconstruction and shows great insensitivity to noise, and can be effectively solved by the Alternating Direction Method of Multipliers (ADMM) algorithm. In this work, the ADMM method of CS reconstruction is used in multi-shot diffusion imaging and proved that it can provide higher reconstruction quality.
Purpose
Multi-shot techniques can help to achieve high
spatial resolution in diffusion imaging. However, due to the application of
diffusion gradients, phase errors are induced by shot-to-shot motions, which
need to be corrected during the reconstruction process. Some phase correction
approaches have been proposed, such as SENSE+CG [1], POCS-ICE [2],
and PR-SENSE [3]. To summarize, SENSE+CG and POCS-ICE try to solve
the optimization problem, $$$\min||Ax-b||_2^2$$$ , using traditional numerical method conjugate gradient (CG)
or POCS. In SENSE+CG, due to the inaccurate estimation of the phase errors,
which aggravate the ill-condition of the inverse problem, the convergence
behavior is unstable [4]. And for PR-SENSE, it adds total variation
(TV) penalty to weaken the
influence of the ill-condition and solves the inverse problem using a method
based on quasi-Newton form. For PR-SENSE and POCS-ICE, the phase errors are
both estimated from the low resolution images of different shots, thus the choices
of the thresholds of the frequency can affect the reconstruction results and may
induce the problem of blurring. This study evaluates the influence of different
thresholds to image quality and proposes a new method based on the ADMM
algorithm [5] used in CS to relieve the blurring problem and achieve
higher image quality.
Methods
(1) ADMM+TV: In multi-shot DWI, the acquired k-space data $$$D$$$ can be expressed as $$$D=FSPf=Kf$$$, in which $$$f$$$ is the diffusion-weighted image to be reconstructed, $$$P$$$ is the exponential of the motion-induced phase errors, $$$S$$$ is the coil sensitivity map and $$$F$$$ is the Fourier transform[3]. The optimization problem of CS with TV-norm can be expressed as: $$$\min||\overrightarrow{\triangledown}f||_{1} s.t. Kf=D$$$, thus the objective function can be expressed as: $$$\min||\overrightarrow{\triangledown}f||_{1}+\lambda/2||Kf-D||_2^2$$$ (λ is the regularization parameter). This objective function can be solved using the ADMM algorithm [5], which is effective and easy to be adopted to solve $$$l_{1}-norm$$$ problem. The unknown operator $$$P$$$ is obtained using the same method in PR-SENSE, which is computed from the phase of the low-resolution image of each shot. (2) SMD: The Sum Modulus Difference (SMD) method [6] is used to define the sharpness of an image or a region of an image, which is defined as $$$SMD=\sum|f(x,y)-f(x,y-1)|+\sum|f(x,y)-f(x-1,y)|$$$ and $$$f(x,y)$$$ denotes the intensity of the image at position $$$(x,y)$$$. The larger the value of SMD, the sharper the image, thus the less of the blur. This method is used to characterize the blurring degree of the images reconstructed in in-vivo experiments. (3) Numerical simulation: A noise-free T1 weighted digital phantom with matrix size of 256×256 downloaded from BrainWeb (http://www.bic.mni.mcgill.ca/brainweb/) was used to generate the simulation data (see Ref. 3 for details of the simulation). (4) In vivo experiment: Brain DTI data were acquired on a Philips 3T scanner (Philips Healthcare, Best, The Netherlands) using an 8-channel RF coil. A spin-echo diffusion weighted spiral sequence without navigator was used. The imaging parameters were: the number of spiral shots= 6, readout duration= 24ms, b= 800s/mm2, FOV= 212×212mm2, slice thickness= 4mm, TR/TE= 2680/54ms, in-plane resolution= 0.95×0.95 mm2. (5) Reconstruction parameters: Different thresholds of frequency were used for ADMM+TV, PR-SENSE and POCS-ICE, and were defined as ratios, such as 1/2 or 2/3 of the maximum frequency. For PR-SENSE and ADMM+TV, the same regularization parameters (0.01) were used to minimize the influence of λ and the detailed determination of λ can be found from Ref. 3.Results and Discussion
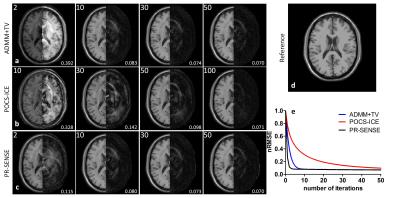
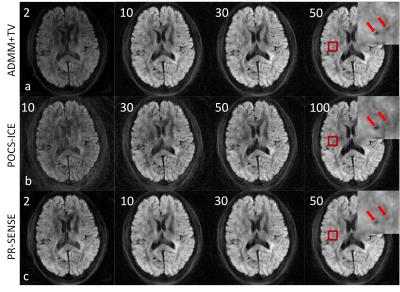
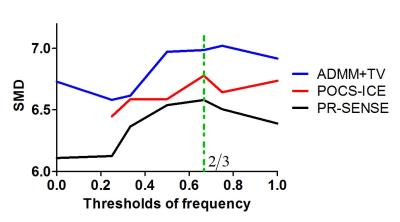
(1) Numerical Simulation: One set of the simulation results are shown in Fig.1, which shows that the proposed method can correct the artificially introduced phase errors effectively and converges faster than POCS-ICE. (2) In vivo experiments: One set of the typical diffusion weighted images reconstructed by the three methods with a frequency threshold of 2/3 are shown in Fig. 2. The image at the right-upper corner of each row shows the magnified result of the region in the red square, in which the black holes indicate the sharpness of the image. Fig. 3 shows the SMD values in the red regions by these three methods using different frequency thresholds. The values from the ADMM+TV method are always bigger than by the other two methods, which means that it can alleviate the blurring problem more effectively. For all the three methods, 2/3 can be a good choice for the threshold. These results indicate that ADMM+TV can preserve more detailed information and is more accurate than POCS-ICE and PR-SENSE.Conclusion
In this study, a method based on the scheme of CS reconstruction called ADMM+TV is proposed for the multi-shot navigator-free DWI and shows a fast convergence speed and better image quality than the existing POCS-ICE and PR-SENSE.Acknowledgements
No acknowledgement found.References
[1] Truong TK et al., MRM 2014; 71(2): 790.
[2] Guo H et al., MRM 2016; 75(1): 169.
[3] Hu Z et al., MRM, 2016.
[4] Qu P et al., MRM 2005; 54(4):1040.
[5] Boyd et al., Foundations and Trends in Machine Learning, 2011, 3(1): 1.
[6] Jarvis R A, Microscope, 1976, 24(2): 163.
Figures