3345
A measurement weighting scheme for optimal powder average estimation1Medical Radiation Physics, Lund University, Lund, Sweden, 2Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States, 3Department of Biomedical Engineering, Linköping University, Linköping, Sweden, 4Center for Medical Image Science and Visualization, Linköping University, Linköping, Sweden
Synopsis
The powder-averaged signal is used in several analysis techniques in diffusion MRI. Assuming uniformly distributed diffusion encoding directions, it is calculated simply as the arithmetic signal average. However, perfectly uniform sampling is generally unattainable.
We demonstrate how non-uniformity can be accounted for by using weighted signal averaging, and we describe how optimal weights can be calculated for existing diffusion encoding schemes to yield improved accuracy of the powder average estimate.
Purpose
Several diffusion MRI methods use “powder averaging” [1] to estimate the rotation invariant signal that would be observed if the compartments of the sample were randomly oriented [2-6]. A natural requirement of a powder average is that it is rotation invariant.
Here, we propose a method for optimizing weights for existing sets of directions, and show that such weights yield improved rotation invariance which is beneficial for the accuracy of the estimated powder average.
Methods
The simplest strategy is to measure in as many ‘uniformly’ distributed orientations as can be afforded, and compute the average of these measurements. However, perfectly uniform sets of directions are rare. Instead, a weighted average can be used to account for the non-uniformity in most directional schemes. For a given diffusion encoding strength the powder averaged signal $$$(\overline{S})$$$ is $$\overline{S} = 1/n_{dir} \cdot \sum_{i=1}^{n_{dir}} {w_i \cdot S_i },$$ where $$$n_{dir}$$$ is the number of directions and $$$w_i$$$ are the weights corresponding to the signal along the $$$i$$$:th direction $$$S_i$$$. To find an optimal set of weights, we define a measure of the rotation variance. A natural approach is to express the true continuous signal, $$$c(\mathbf{\hat x})$$$, in a spherical harmonics basis, $$$a_{nk}$$$, acccording to
$$f_{nk} = \int{a_{nk}(\mathbf{\hat x}) c(\mathbf{\hat x})}\text{d}\mathbf{\hat x},$$
where $$$n$$$ is the harmonics order and $$$k$$$ indicates a specific function of that order. The rotational variance of a set of unit vectors that specify the measured directions ($$$\mathbf{y}_i$$$) can be analyzed in a similar way. The spherical harmonics components, $$$g_{nk}$$$, of $$$\mathbf{y}_i$$$ is
$$g_{nk}=\sum_i^{n_{dir}}{w_i b_{nk}(\mathbf{y}_i)}.$$
Comparing this to Fourier analysis of a 1-dimensional signal using equidistant sampling, the projections of the iso-weighted sampling on the Fourier basis will be non-zero for frequencies outside the interval 0 to twice the Nyquist frequency, hence no weighting is necessary. Since perfectly uniform samples on the sphere are not know, introducing weights may improve rotation invariance. An optimal set of weights $$$(\mathbf{w}_0)$$$ is readily found by solving the following least squares problem [11]
$$\mathbf{w}_0=\text{argmin}[(\mathbf{B}\mathbf{w}-\mathbf{g}_0)^\text{T}\mathbf{V}(\mathbf{B}\mathbf{w}-\mathbf{g}_0)]=(\mathbf{B}^\text{T}\mathbf{V}\mathbf{B})^{-1}(\mathbf{V}\mathbf{B})^\text{T}\mathbf{g}_0,$$
where $$$\mathbf{B}$$$ is a matrix of the spherical harmonics basis sampled at the orientations $$$\mathbf{y}_i$$$; $$$\mathbf{V}$$$ is a diagonal matrix that contains the weight attached to a goodness-of-fit for each spherical component; and $$$\mathbf{g}_0$$$ holds the desired projection value for each spherical component. For the powder average case $$$\mathbf{g}_0$$$ is non-zero only for $$$b_{01}$$$ (constant zero order basis function). The rotation invariance of $$$\mathbf{y}_i$$$ was also gauged in terms of the coefficient of variation (CV) of $$$\overline{S}$$$ over $$$10^6$$$ random rotations of the object according to ref. 7 (rotational invariance is when the CV is negligible compared to other sources of variance, such as signal noise). The signal from a single diffusion tensor at $$$b=$$$1000 s/mm2 with axial and radial diffusivities of 2.0 and 0.2 µm2/ms was simulated along $$$n_{dir}\in[4, 64]$$$ directions (optimized on the half-sphere [8] $$$10^3$$$ times in ExploreDTI [9] to avoid local minima).
Results
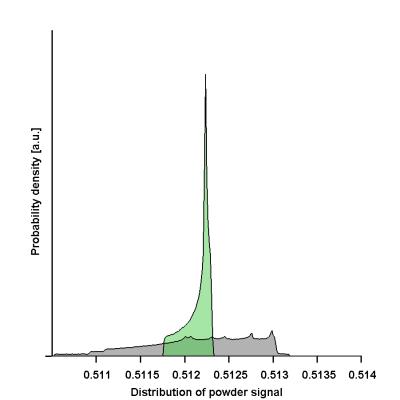
Fig.1 shows the impact of using a weighted powder average on the rotation variance of the signal. It clearly demonstrates that an optimal weighting yields an improved rotational invariance (CV decreases and the distribution of estimated $$$\overline{S}$$$ has lower variance). Fig.2 shows how the difference between the sampling scheme and harmonic order is affected by weighting, which indicates that there is an upper bound where the weighting no longer improves the result. Fig.3 demonstrates a case where using more directions reduces the precision of the powder averaged signal. Fig.4 shows the direction schemes that yield superior rotation invariance in the investigated interval ($$$n_{dir}=$$$ 16 and 61) along with color coded weights.Discussion and conclusions
In conclusion, we have provided a method for optimal weighting of signal for the calculation of the powder average, and demonstrated that it is beneficial in a simulated example. We have also demonstrated that more directions do not guarantee an improved accuracy. This is especially true around $$$n_{dir}=$$$ 6, 16 and 61 [10], since these exhibit low rotational variance compared to neighboring sets. Notably, the present methods can be modified to optimize higher order terms, e.g., the 2:nd order to optimize directions for DTI, however, this was outside the scope of this study. A limitation of this study is that the effect of weighting has not been evaluated in actual data where the benefit may be small compared to other sources of variance and bias, such as signal noise. On the other hand the cost of using a weighted average is negligible, and renders higher accuracy.
Acknowledgements
The authors acknowledge funding by Swedish Foundation for Strategic Research project number AM13-0090.References
[1] Edén, Concepts in Magnetic Resonance Part A 18A (1), 24-55 (2003); [2] S. Lasic et al., Frontiers in Physics 2, 11 (2014); [3] Szczepankiewicz et al., Neuroimage 104, 241-252 (2015); [4] Lawrenz and J. Finsterbusch, Magn. Reson. Med. 73 (2), 773-783 (2015); [5] Jespersen et al., NMR Biomed. 26 (12), 1647-1662 (2013); [6] McKinnon et al., Magn. Reson. Imaging (2016); [7] Szczepankiewicz et al., Proc. Intl. Soc. Mag. Reson. Med. 24, 2065 (2016). [8] Jones et al., Magn. Reson. Med. 42 (3), 515-525 (1999). [9] Leemans, Proc. Intl. Soc. Mag. Reson. Med., 2009 [10] E. L. Altschuler et al., Phys. Rev. Lett. 78 (1997). [11] Knutsson et al., Proc. of the 11th Scand. Conf. on Image Analysis: Greenland, SCIA , 1999, p185-193.Figures
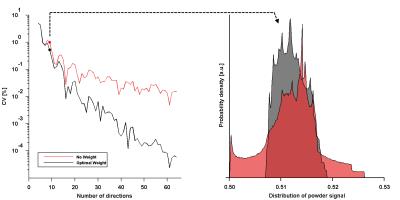
Fig. 2 | The plot shows the root-mean-square (RMS) of the projection of the sampling pattern onto different spherical harmonics orders (lower RMS value is better). Graphs are shown for $$$n_{dir}=16$$$ (original in blue, optimized in red) and $$$n_{dir}=61$$$ (original in yellow, optimized in purple). Note that the benefit of weight optimization is most prominent in the intermediate range of spherical harmonic orders, i.e. weighting accounts for the rotation variance of intermediate order harmonics, but at sufficiently high orders, the system is irrecoverably under-sampled, and the weighting has no effect.