3342
Towards Achieving the Optimal SNR Efficiency for 3D Multi-shot Diffusion-Weighted Echo-Planar Imaging1Department of Diagnostic Radiology, The University of Hong Kong, Hong Kong, Hong Kong, 2The State Key Laboratory of Brain and Cognitive Sciences, The University of Hong Kong, Hong Kong, Hong Kong, 3Department of Biomedical Engineering, University of Arizona, Tucson, AZ, United States, 4Brain Imaging and Analysis Center, Duke University Medical Center, Durham, NC, United States
Synopsis
Due to the assumption of 2D phase variations, the feasible maximum slab thickness is relatively thin (e.g. < 25 mm) for 3D multi-shot diffusion-weighted echo-planar imaging. We have thus proposed a new method in another study to correct for 3D inter-shot phase variations, thereby significantly increasing the feasible maximum slab thickness. In this study, we have demonstrated by simulations and experiments that slab thickness can be significantly increased to allow whole brain coverage with a TR that achieves optimal SNR efficiency.
Purpose
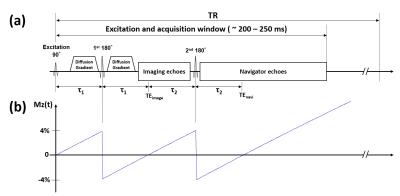
3D multi-slab multi-shot diffusion-weighted echo-planar imaging (msDW-EPI) has been demonstrated to be useful for achieving high-resolution DWI with isotropic voxel1-4. Similar to 2D msDW-EPI acquisition, phase variation along the z direction is typically assumed to be negligible. However, 2D phase correction method using navigator echo can eliminate aliasing artifacts1-4 only when the slab thickness is relatively thin (e.g. < 25 mm), thus substantially limiting the feasible maximum slab thickness. Together with the fact that the TR for optimal SNR efficiency of 3D msDW-EPI was ranged between 1 to 2 sec5 and that acquisition window is usually long (see Figure 1a), the brain coverage will be limited, rendering the technique not clinically applicable. We have thus proposed a new 3D phase correction method, termed 3D-MUSER, in another study to account for the 3D inter-shot phase variations in order to significantly improve the feasible maximum slab thickness6. The aim of this study is therefore to demonstrate that our 3D-MUSER would allow whole brain coverage with optimal SNR efficiency for 3D msDW-EPI. First, we investigate 1) the optimal flip angle (FA) for different TR, and simulate 2) the SNR efficiency (SNReff-3D) for any slab thickness. Second, we demonstrate that the substantial increase in maximum slab thickness achieved by 3D-MUSER can enable whole brain coverage with optimal SNReff-3D for arbitrary slab number.Methods
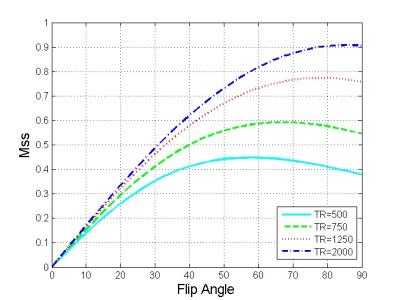
Simulation of T1-saturation effect: To investigate the effect of the dual refocusing RF pulses in our 3D msDW-EPI sequence (see Figure 1b) on the steady-state signal (Mss), the T1-recovery of the longitudinal magnetization (Mz) was simulated with the following parameters: τ1 = τ2 = 30 ms, T1 of white-matter = 800 ms, TR = [500, 5000] ms, and FA = [0, 90]°.
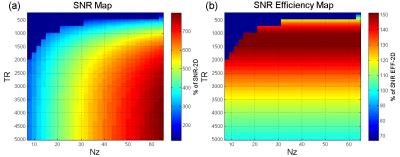
Simulation of SNR efficiency: The SNR3D and SNReff-3D for various TRs and numbers of kz encoding steps were simulated using the Mss from previous simulation. The SNR2D of 2D msDW-EPI (with same number of ky segments and TR of 5000 ms) was used as a standard for normalizing the SNR3D. The desired slice coverage along was assumed to be 64 slices, and the whole acquisition window was 200 ms.
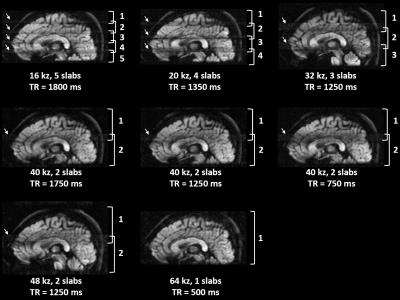
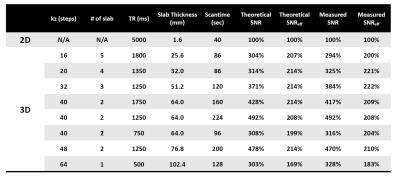
Imaging experiments: All data were acquired from a healthy subject at 1.5T GE HDxt MRI scanner using an 8-channel head coil. Eight sets of 3D msDW-EPI data were acquired with different TR, number of slabs per TR, and kz encoding steps with 20% oversampling (see table in Figure 5). The desired converge of brain along z was 64 slices with 1.6 mm isotropic voxel size. Other imaging parameters included: FOV = 20.4 cm, ky segment = 4, TE = 62 ms, and b-value = 1000 s/mm2 along z. One set of 2D msDW-EPI data with same voxel size and NEX = 2 was also acquired for SNR comparison.
Data reconstruction and analysis: All 3D multi-slab data were reconstructed by using our newly proposed 3D-MUSER algorithm6 and combined using weighted averaging. All measured SNRs were calculated from an ROI placed in white matter. The SNR efficiencies were subsequently calculated by considering the scan time for each volume.
Results
Figure 2 shows the Mss of 3D msDW-EPI for different TRs and FAs. Figure 3 shows the theoretical SNR3D and SNReff-3D for different TRs and number of kz encoding steps. The blue area in each map represents imaging parameters that failed to achieve whole brain coverage. Figure 4 shows DWI images in sagittal plane reformatted from different data sets. Figure 5 shows the SNR3D and SNReff-3D measured from experiment data.Discussion & Conclusion
Here we demonstrate that the improved maximum slab thickness of 3D msDW-EPI can enable whole brain coverage with small number of thick slabs, thereby achieving higher SNReff-3D with optimal TR (i.e., 1250 ms at 1.5T). The derived optimal FA for 3D msDW-EPI sequence shows a subtle influence on Mss (less than 10% for TR>500ms), which is not critical for optimizing SNReff-3D, especially for TR > 1000 ms. The experimental SNR3D and SNReff-3D are in good agreement with theoretical prediction, thus supporting the notion that optimal SNReff-3D can be achieved with flexible number of slabs with larger thickness. In addition, the maximum number of multiple slabs for a given TR also depends on hardware configurations. In an extreme case without optimization of SNReff-3D, 3D-MUSER can enable single-slab acquisition with shorter TR (i.e., 500ms) to avoid slab boundary artifact (Figure 4). In conclusion, the significantly improved maximum slab thickness can offer a wide range of choices for imaging parameters for different MRI scanners, thereby improving SNReff-3D and benefiting artifact reduction in 3D msDW-EPI acquisition.Acknowledgements
No acknowledgement found.References
1. Chang HC, Sundman M, Petit L, Guhaniyogi S, Chu ML, Petty C, Song AW, Chen NK. Human brain diffusion tensor imaging at submillimeter isotropic resolution on a 3Tesla clinical MRI scanner. Neuroimage 2015;118:667-675.
2. Engstrom M, Skare S. Diffusion-weighted 3D multislab echo planar imaging for high signal-to-noise ratio efficiency and isotropic image resolution. Magn Reson Med 2013;70(6):1507-1514.
3. Frost R, Miller KL, Tijssen RH, Porter DA, Jezzard P. 3D multi-slab diffusion-weighted readout-segmented EPI with real-time cardiac-reordered K-space acquisition. Magn Reson Med 2014;72(6):1565-1579.
4. Van AT, Hernando D, Sutton BP. Motion-induced phase error estimation and correction in 3D diffusion tensor imaging. IEEE Trans Med Imaging 2011;30(11):1933-1940.
5. Engstrom M, Martensson M, Avventi E, Skare S. On the signal-to-noise ratio efficiency and slab-banding artifacts in three-dimensional multislab diffusion-weighted echo-planar imaging. Magn Reson Med 2015;73(2):718-725.
6. “Three-Dimensional Multiplexed Sensitivity Encoding and Reconstruction (3D-MUSER): 3D Phase Correction for 3D Multi-shot DWI”, submitted to ISMRM 2017.
Figures