3341
Determination of the optimal set of b-values for ADC mapping under a Rician noise assumption1Laboratorio de Procesado de Imagen, Universidad de Valladolid, Valladolid, Spain, 2Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3Medical Physics, University of Wisconsin-Madison, Madison, WI, United States
Synopsis
Mapping of the apparent diffusion coefficient (ADC), estimated from a set of diffusion-weighted (DW) images acquired with different b-values, often suffers from low SNR, which can introduce large variance in ADC maps. Unfortunately, there is no consensus on the optimal b-values to maximize the noise performance of ADC map. In this work, we determine the optimal b-values to maximize the noise performance of ADC mapping by using a Cramér-Rao Lower Bound (CRLB) approach under realistic noise assumptions. The strong agreement between the CRLB-based analysis, Monte-Carlo simulations, and ADC phantom experiment, suggests the utility of this approach to optimize DW-MRI acquisitions.
Purpose
Mapping of the apparent diffusion coefficient (ADC) from a set of diffusion-weighted (DW) images acquired with different b-values, often suffers from low SNR, which can introduce large variance in ADC maps. Unfortunately, there is currently no consensus on the optimal set of b-values to maximize the noise performance (ie: minimize the variance) of ADC mapping. The purpose of this work is to optimize the set of b-values for ADC mapping, using Cramér-Rao Lower Bound1 (CRLB) analysis under the assumption of realistic Rician distributed data, noise distribution commonly present in MRI2.Methods
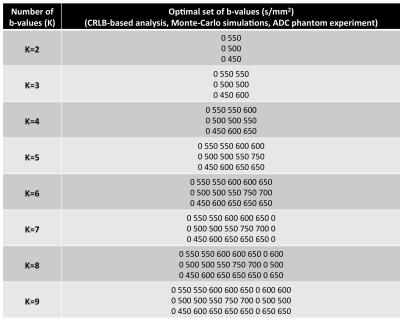
Determination of optimal b-values: The ADC mapping signal model is described by $$$S(b)=S_0e^{-bADC}$$$. In order to maximize the noise performance of ADC estimation we optimize the set of b-values via the CRLB approach. Such an approach was previously employed, in related contexts, in Refs3,4 under Gaussian noise assumptions, and by Ref5 for the Kurtosis model under a Rician assumption. Given a set of independent Rician distributed observations of the ADC signal model, Sk where k∈[1,...,K], with the same noise level, the CRLB of the ADC (CRLBADC) is given by the element (2,2) of the inverse of the Fisher Information Matrix1 (Eq. 1), where In is described in Ref5. Therefore, for a given target ADC, noise level, and number of b-values (K), the determination of the set of K b-values that maximizes the noise performance of the ADC estimation is performed by an iterative brute force algorithm. The iterative algorithm starts from a set of b-values composed only of b-value=0 s/mm2 and iteratively adds to the set the b-value that achieves minimum CRLBADC among a large set of b-value candidates. The proposed algorithm iterates until a set of K b-values is completed. Table 1 shows the pool of candidate b-values and other parameters employed.
Eq. 1: $$FIM=\begin{bmatrix}\sum_{k=0}^Ke^{-2b_kADC}I_n(S_k,\sigma)&-\sum_{k=0}^KS_0b_ke^{-2b_kADC}I_n(S_k,\sigma)\\-\sum_{k=0}^KS_0b_ke^{-2b_kADC}I_n(S_k,\sigma)&\sum_{k=0}^KS_0^2b_k^2e^{-2b_kADC}I_n(S_k,\sigma)\end{bmatrix}$$
Validation of optimal b-values: The sets of b-values obtained theoretically with the proposed method are compared to those obtained experimentally from:
1) Monte-Carlo simulations, which included 13 different true ADCs (400 simulated pixels each) with a Rician distribution and parameters from Table 1.
2) An ADC phantom6 experiment consisting of 13 vials with different ADCs at room temperature. The DW-MRI acquisition was performed at 1.5T (GE Healthcare, Waukesha, WI) using a standard single shot EPI sequence with the following parameters: slice thickness of 5 mm, FOV=24cm x 24cm, matrix size of 144x144, TE=111 ms, and 41 b-values uniformily distributed between 0-2000 s/mm2. Further, this acquisition was repeated 16 consecutive times (discarding the first three repetitions to avoid steady-state effects) to enable voxel-wise determination of ADC estimation statistics.
The optimal sets of b-values for the Monte-Carlo simulations and the ADC phantom experiment were obtained iteratively. At each iteration, the b-value that minimizes the variance of the ADC estimation among all candidate b-values is added to the selected set. The procedure is analogous to the one employed in the theoretical optimization, but using the experimental variance instead of the CRLBADC (note that 13 repetitions are available for both, the Monte-Carlo simulations and the ADC phantom experiment). Each ADC estimation was performed pixel-wise via a Maximum Likelihood7 estimator (ML).
Results
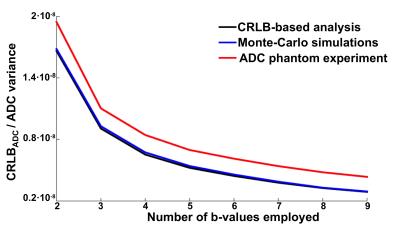
Table 2 shows the optimal sets of b-values obtained from the CRLB-based theoretical analysis, Monte-Carlo simulations, and ADC phantom experiment for one of the vials (ADC=2.1·10-3mm2/s). Further, Figure 1 shows, for the same vial, the evolution of the CRLBADC and experimental variances with respect to the number of b-values employed. Figure 2 shows a color-coded comparison of the optimal sets of b-values for all the vials in Table 1.Discussion
Results indicate a strong agreement between optimal the sets of b-values obtained using the proposed CRLB-based theoretical analysis and those found experimentally both by the Monte-Carlo simulations and by the ADC phantom experiment. This illustrates the potential of the proposed CRLB-based approach to maximize the noise performance (minimize the variance) of ADC mapping by optimizing the choice of acquired b-values. In order to achieve a procedure that is suitable for the selection of the set of b-values in clinical settings, further validation is still required, considering realistic distributions of target ADCs, the effect of T2 relaxation, and in-vivo results.Conclusion
The optimization of the b-values is critical to maximize the noise performance (ie: minimize variance) of the ADC estimation in DW-MRI. The proposed approach may help optimize and standardize DW-MRI acquisitions by computing the optimal set of b-values for a target ADC.Acknowledgements
The authors acknowledge grant TEC2013-44194-P from the Ministerio de Economía y Competitividad of Spain.References
1. Karlsen OT, et al. Parameter Estimation From Rician-Distributed Data Sets Using a Maximum Likelihood Estimator: Application to T1 and Perfusion Measurements. Magn Reson Med. 1999;41(3):614-623.
2. Aja-Fernández, et al. Statistical Analysis of Noise in MRI. Springer, 2016.
3. Brihuega-Moreno O, et al. Optimization of Diffusion Measurements Using Cramer-Rao Lower Bound Theory and Its Application to Articular Cartilage. Magn Reson Med. 2003;50(5):1069-1076.
4. Leporq B, et al. Optimization of the Intra-voxel Incoherent Motion Imaging at 3.0 Tesla for Fast Liver Examination. J Magn Reson Imaging. 2015;41(5):1209-1217.
5. Poot DH, et al. Optimal Experimental Design for Diffusion Kurtosis Imaging. IEEE Trans Med Imaging. 2010;29(3):819-29.
6. High Precision Devices, Inc. Quantitative (qMRI) QIBA DWI Diffusion Phantom. http://www.hpd-online.com/diffusion-phantom.php. Accessed October 26,2016.
7. Sijbers J, et al. Maximum-Likelihood Estimation of Rician Distribution Parameters. IEEE Trans Med Imaging. 1998; 17(3):357-361.
Figures
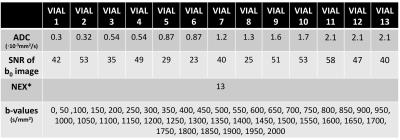
Table 1: Parameters of interest obtained from the ADC phantom experiment. These values were also applied for CRLB-based optimization as well as in the Monte-Carlo simulations.
*The CRLB-based optimization is under the assumption of NEX=1.