3340
Optimal design of motion-compensated diffusion gradient waveforms1Laboratorio de Procesado de Imagen, Universidad de Valladolid, Valladolid, Spain, 2Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3Medical Physics, University of Wisconsin-Madison, Madison, WI, United States
Synopsis
Diffusion-Weighted MRI (DW-MRI) often suffers from motion-related artifacts in organs that experience physiological motion. Importantly, organ motion during the application of diffusion gradients results in signal losses, which complicate image interpretation and bias quantitative measures. Motion-compensated gradient designs have been proposed, however they typically result in substantially lower b-values or severe concomitant gradient effects. In this work, we develop an approach for design of first- and second-order motion-compensated gradient waveforms based on a b-value maximization formulation including concomitant gradient nulling, and we compare it to existing techniques. The proposed design provides optimized b-values with motion compensation and concomitant gradient nulling.
Introduction
Diffusion-Weighted MRI (DW-MRI) is widely used in brain and body imaging. However, DW-MRI often suffers from motion-related artifacts, particularly in organs that experience substantial physiological motion1 (eg: heart and liver). In these organs, the presence of macroscopic tissue motion during the application of diffusion gradients can result in signal voids, which complicate the interpretation of DW images and introduce bias and variability in the quantification of diffusion parameters2. For these reasons, there is significant interest in the development of motion-compensated (eg: nth order moment nulled) diffusion gradient waveforms. A recent method for the design of first and second order moment nulled diffusion gradient waveforms based on a constrained optimization formulation, termed Convex Optimized Diffusion Encoding3 (CODE), has demonstrated excellent promise for DW-MRI in heart and liver. However, it is unclear whether CODE results in optimal waveforms (ie: maximum b-value for a given echo time). Furthermore, due to the asymmetry of CODE waveforms, they strongly suffer from concomitant gradient4 (CG) effects, which may introduce severe artifacts. Therefore, the purpose of this work is to formulate a technique for direct b-value maximization for the design of optimal diffusion gradient waveforms. Further, the proposed formulation also includes correction for CG effects.Methods
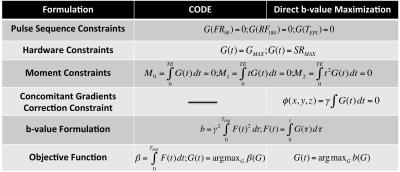
Several motion-compensated symmetric diffusion gradient waveforms have been designed to null the first (M1) or second order (M2) gradient moments3,5,6. However, these traditional designs do not maximize the b-value for a given TE, and therefore result in severely reduced b-values if motion compensation is desired. Recently, a formulation of the gradient waveform design as a constrained optimization (CODE) was introduced. CODE seeks to provide the shortest waveform that achieves a given b-value by formulating the diffusion gradient waveform design as a constrained maximization problem. In principle, CODE seeks to maximize the b-value, defined as $$$b=\int_{0}^{T_{Diff}}F(t)^2 dt$$$, where $$$F(t)=\int_{0}^{t}G(\tau) d\tau$$$, and G(t) is the gradient waveform. However, in order to facilitate the constrained optimization problem CODE reformulates the problem to maximize an alternative function, which may lead to suboptimal gradient waveforms. In order to overcome this limitation, we propose a new approach ('Direct b-value Maximization') that directly optimizes the b-value based on the same formulation and constraints as CODE, as shown in Table 1.
Further, we also consider the effect of CGs on the gradient waveform. CGs appear every time we generate a magnetic field gradient as described by Maxwell's equations4, and result in a spatially-varying dephasing along the three axes which depends on the applied gradients, $$$\Phi(x,y,z)=\gamma\int{B_c(x,y,z,t) dt}$$$, where Bc is described in Ref2. To correct for the presence of CGs, we incorporate Φ(x,y,z)=0 as a constraint in the proposed formulation.
In this work, the b-values achievable over a range of TEs with the proposed Direct b-value Maximization (with and without CG correction) are compared to previously proposed gradient waveform designs for three different types of constraints: zero moment nulling (M0=0, as required for any diffusion encoding waveform), first order moment nulling (M0=M1=0), and second order moment nulling (M0=M1=M2=0).
Results
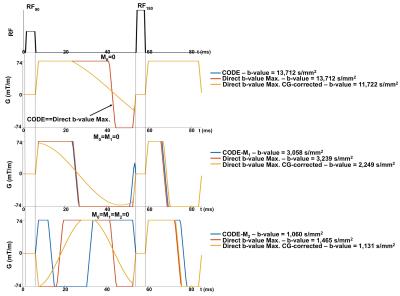
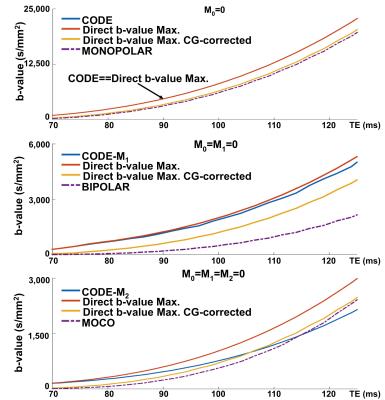
Figure 1 shows waveforms generated by the proposed Direct b-value Maximization method (with and without CG nulling), as well as CODE waveforms. These examples illustrate the higher b-value achievable with Direct b-value Maximization compared to CODE. Figure 2 demonstrates higher b-values with the proposed method for M0=M1=0 and M0=M1=M2=0, while the waveforms are identical to CODE designed waveforms for M0=0. Although CG correction results in a b-value reduction, the proposed CG-corrected method still provides higher b-values than traditional designs, like MONO, BIPOLAR, and motion-compensated (MOCO6).Discussion
These preliminary results illustrate the potential of the proposed formulation to maximize the b-value achievable with motion-compensated diffusion gradient waveforms subject to hardware and timing constraints. Further, inclusion of CG correction also improves the traditional designs, likely by eliminating the dead time between radio frequency pulses. This formulation provides optimized motion-compensated gradient waveforms, with potential application of DW-MRI in organs that experience substantial physiological motion2,3. However, validation of these results in phantom and in-vivo studies is still required.Conclusion
We have developed an optimized approach for the design of motion-compensated diffusion gradient waveforms. The proposed method maximizes the achievable b-value while nulling the first and second order moments, as well as nulling the effects of CGs. This approach may have application for motion-compensated DW-MRI in the heart, liver, and other organs that experience substantial physiological motion.Acknowledgements
The authors acknowledge grant TEC2013-44194-P from the Ministerio de Economía y Competitividad of Spain.References
1. Taouli B, et al. Diffusion-weighted MR Imaging of the Liver1. Radiology. 2009;254(1):47-66.
2. Murphy P, et al. Error Model for reduction of cardiac and respiratory motion effects in quantitative liver DW-MRI. Magn Reson. Med. 2013;70(5):1460-1469.
3. Aliotta E, et al. Convex Optimized Diffusion Encoding (CODE) Gradient Waveforms for Minimum Echo Time and Bulk Motion-Compensated Diffusion Weighted MRI. Magn Reson Med. 2016;00:00-00.
4. Bernstein MA, et al. Concomitant Gradient Terms in Phase Contrast MR: Analysis and Correction. Magn Reson Med. 1998;39(2):300-308.
5. Simonetti OP, et al. Significance of the Point of Expansion in the Interpretation of Gradient Moments and Motion Sensitivity. J Magn Reson Imaging. 1991;1(5):569-577.
6. Stoeck CT, et al. Second-Order Motion-Compensated Spin Echo Diffusion Tensor Imaging of the Human Heart. Magn Reson Med. 2016;75:1669-1676.
Figures