3339
Randomizing simultaneously excited slice groups in SMS to reduce slice leakage artifacts in diffusion MRI1Biophysics, Medical College of Wisconsin, Milwaukee, WI, United States, 2Radiology, Medical College of Wisconsin, Milwaukee, WI, United States, 3Neurosurgery, Medical College of Wisconsin, Milwaukee, WI, United States
Synopsis
Simultaneous Multi-slice (SMS) techniques excite multiple slices simultaneously to accelerate MRI data acquisition. However, slice separation during image reconstruction is not exact and results in coupling between separated voxels. While this may not be critical for most anatomic imaging methods, small but consistent leakage of information from another slice in a DTI dataset will cause bias in diffusion parameter estimates. Here, we propose a randomized-slice pairing technique to alleviate this problem in diffusion MRI acquisitions.
Purpose
Simultaneous Multi-slice (SMS) techniques excite multiple slices simultaneously and separate the overlapping slices using a mathematical model. However, this slice separation is not exact and leads to information leakage between simultaneously excited slices1,2. Thus, measurements in a voxel will be affected by the residues from the overlapped slices. In diffusion MRI techniques, such as DTI or Diffusion Kurtosis Tensor Imaging (DKTI), this introduces a significant problem. If the same group of slices are excited simultaneously across all diffusion weighted images, the same voxels are mixed every time, and the diffusion estimates in each voxel are biased by the slice leakage.
Here,
we propose a novel adaptation of SMS to mitigate the effects of slice leakage
in diffusion metrics. We randomize which slices are simultaneously excited
across different diffusion weighted images. Since overlapping slices will be
different for each diffusion weighted image, residual effects from imperfect
slice separation will appear as random noise. With enough diffusion directions
and weightings, the model parameter estimation should be robust against this
random noise. We refer to this method as
randomized-slice (rs-)SMS. The method can be used in conjunction with various SMS
techniques. This will allow SMS to be employed to reduce acquisition time in diffusion
MRI experiments, while minimizing the notorious slice leakage problem.
Methods
With a pre-processed diffusion MRI data set from the HCP database3, a whole-brain simulation of SMS and rs-SMS acquisitions quantified the effect of slice leakage on diffusion metrics. A sagittal slice was selected for analysis. To simulate SMS data, chosen slices were overlapped in a blipped-CAIPIRINHA-like fashion with a FOV/2 shift in the phase encode direction between the slices. For conventional SMS, the overlapped slices are the same for each diffusion weighted image volume with a separation of 5.6 cm. For rs-SMS, the primary slice was fixed and a random number generator determined the overlapping slice for each diffusion weighted image from a range of slices satisfying the minimum slice separation of 4cm.
Slice leakage was simulated by adding the signal from the overlapped slice scaled by a leakage factor. Leakage factor was adjusted between 0% to 20%. The slice that was contaminated by the leakage was processed with a diffusion kurtosis tensor algorithm developed in-house based on the method published by Jensen et al.4. Diffusion metrics of interest were mean diffusivity (MD), fractional anisotropy (FA), and mean kurtosis (MK).
Results
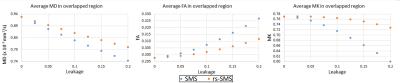
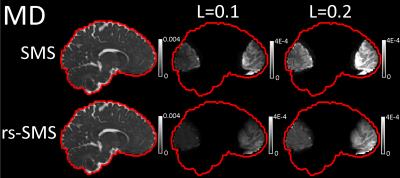
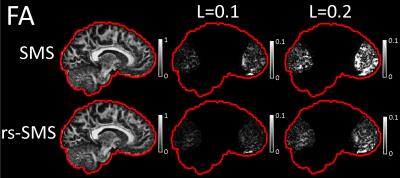
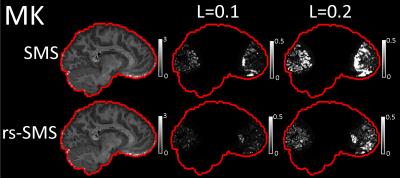
Mean metric values as a function of leakage factor in the overlapped regions are presented in Figure 1. Estimation errors occurred where the slices overlapped in the blipped-CAIPI simulation. For each metric, rs-SMS generated smaller errors caused by slice leakage compared to conventional SMS. The relation between the amount of slice leakage and the magnitude of errors was nonlinear. At a leakage factor of 0.1, SMS had percent errors of 10.6%, 3.2%, and 7.1% for MD, FA, and MK, respectively. In contrast, rs-SMS had errors of 7.2%, 1.5%, and 0.7% for the respective metrics. At 0.2 leakage factor, the MK for rs-SMS had 5.4% error compared to 22% error for SMS. Metric maps for SMS and rs-SMS without leakage as well as difference maps for 0.1 and 0.2 leakage factors are presented for MD (Figure 2), FA (Figure 3), and MK (Figure 4).Discussion
We introduced a novel approach that improved the accuracy of DKTI parameter estimation when SMS acceleration was employed. It is important to note that this method does not reduce the slice leakage. Instead, it reduces the bias in model parameter estimates by making the leakage behave like a random noise. This way, a first or second order diffusion model estimation would treat the leakage as residual fitting errors rather than a consistent measurement.
Here we simulated blipped-CAIPI due to its widespread use in diffusion SMS, but this technique could also be applied to other SMS methods. We did not focus on improving reconstruction to reduce leakage. Our goal was to address the problem in the acquisition stage. It should be noted that any reconstruction improvements to reduce this leakage will still benefit from rs-SMS diffusion acquisition.
In summary, rs-SMS was more robust to slice leakage than conventional SMS for each of the diffusion kurtosis metrics. Slice leakage appears to have a nonlinear relationship with error in the metric estimates. Although we only investigated multiband factor of 2, higher acceleration rates may see an even greater improvement with rs-SMS. Optimal slice combinations and higher multi-band factors will be explored in future studies.
Acknowledgements
No acknowledgement found.References
1. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K (2014) Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magnetic Resonance in Medicine 72:93-102.
2. Setsompop K et al. (2013) Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. NeuroImage 80:220-233.
3. Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K (2013) The WU-Minn Connectome Project: An overview. NeuroImage 80:62-79.
4. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K (2005) Diffusional kurtosis imaging: The quantification of non-Gaussian water diffusion by mean of magnetic resonance imaging. Magnetic Resonance in Medicine 53:1432-1440.
Figures