3336
Improved Navigator-free Multi-shot DTI Reconstruction with Inter-image Correlation Constraint1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, China, Beijing, People's Republic of China, 2Vascular Imaging Laboratory, Department of Radiology, University of Washington, Seattle, WA, United States
Synopsis
To improve the image quality for navigator-free multi-shot DTI reconstruction, the inter-image correlation constraint is introduced. Group sparsity and anisotropic sparsity are proposed as two specific implementations, using the POCS-ICE algorithm. Results show that both constraints can improve the image quality with increased SNR. In addition, anisotropy sparsity has less blurring and can better maintain the detailed structures.
Purpose
Multi-shot techniques have been used to achieve high resolution diffusion imaging, using either navigated methods or navigator-free methods. The navigator-free methods, including MUSE [1] and SENSE+CG [2], estimate the phase variations from each shot using parallel imaging, and have higher scan efficiency because no extra navigator is acquired. Recently, POCS-enhanced Inherent Correction of motion-induced phase Errors (POCS-ICE) [3] was proposed to improve the image quality for navigator-free methods, through simultaneous updating of image and phase variations iteratively. Because POCS-ICE has the flexibility to incorporate different types of a priori knowledge, additional constraints can be added to further improve navigator-free multi-shot diffusion imaging. In this study, we propose to use inter-image correlation among different diffusion directions as the constraint, which has been used for DTI acceleration and denoising in previous studies [4, 5].Theory
Using POCS-ICE, the diffusion-weighted image $$$\bf f$$$ and the phase variations $$$\bf P$$$ are simultaneously reconstructed as described in the following equation.
$$$\bf f_\it n, \bf P_ {\it n,m=\rm 1,...\it M}=\rm argmin\sum_{\it m=\rm 1}^{\it M}\sum_{\it c=\rm 1}^{\it Nc}\|\bf F_\it m \bf S_\it c\bf P_\it {m,n} \bf f_\it n-\bf d_{\it m,c,n}\|_\rm 2^2+\lambda\bf\it R\rm(\bf f_\it n\rm )$$$, (1)
where $$$\it n$$$, $$$\it m$$$ and $$$\it c$$$ denote the index of each diffusion direction, shot and channel, respectively. $$$\it M$$$ and $$$\it Nc$$$ denote the total number of shots and channels, respectively. $$$\bf d$$$ is the acquired k-space data. $$$\bf S$$$ is the coil sensitivity. $$$\bf F$$$ is the Fourier encoding. $$$\bf \it R$$$ is the constraint part, with a regularization factor $$$\lambda$$$.
Since the diffusion-weighted images in different directions are highly correlated, e.g., sharing similar image boundaries, they can be jointly reconstructed by incorporating inter-image correlation constraint. Here we propose two specific constraints, group sparsity (GS) and anisotropic sparsity (AS) [4], demonstrated by Equation (2) and (3), respectively.
$$$\bf\it R=\sum_{\it n=\rm 1}^\it N\|\bf Wf_\it n\|_\rm1$$$. (2)
$$$\bf\it R=\sum_{\it n=\rm 1}^\it N\|\bf W(f_\it n- \rm \bf \overline f \rm)\|_\rm1$$$. (3)
Here $$$\it N$$$ denotes the number of directions, and $$$\bf W$$$ denotes the sparsity transform. In Equation (3), $$$\bf \overline f$$$ is the averaged image of all directions, which is considered as the isotropic part in DTI.
Methods
Navigator-free interleaved EPI DTI data were acquired on a Philips 3.0T Achieva TX scanner (Philips, Best, The Netherlands) with an eight-channel head coil. b-value of 1000 s/mm2 and 24 directions were used. FOV=236×236mm2, voxel size=0.80×8×4mm3, TE/TR=113/2500ms. 6 shots were acquired, with a partial Fourier factor of 0.65. In addition, low-resolution DTI data were acquired using single-shot EPI (SS-EPI), with voxel size of 2×2×4mm3, TE/TR of 84/2400ms and SENSE factor of 2. Other parameters were the same as the multi-shot acquisition.
The multi-shot diffusion-weighted images were reconstructed using POCS-ICE without constraints, with GS and AS constraints, respectively, following the flow-chart shown in Fig. 1. The wavelet transform was chosen as the sparsity operator. A soft threshold was used to apply L1-norm minimization, with the threshold of 1x10-4 for both GS and AS.
After the reconstruction, color-coded FA maps (cFA) were calculated using DTI-studio [6]. The reconstructed images from different reconstruction methods and the corresponding FA maps were then compared.
Results and Discussion
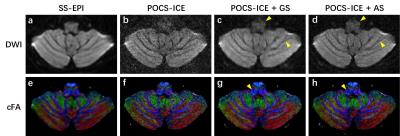
The diffusion-weighted images and cFA from the 6-shot EPI, which were reconstructed using POCS-ICE without constraint, with GS and with AS constraints are shown in Fig. 2. It can be observed that using either GS or AS constraint can improve the image quality, especially increasing the SNR. In addition, using AS constraint shows less blurring and finer structures than GS, which is highlighted with yellow arrowheads. The better performance of AS constraint is probably due to that removing isotropic signals in DTI can boost the sparsity, which has been shown in the previous study [4].Conclusion
In this study, the inter-image correlation constraint was introduced to improve the reconstruction for navigator-free multi-shot DTI. Group sparsity and anisotropic sparsity were proposed as two specific implementations, using the POCS-ICE algorithm. While both constraints can improve the image quality with increased SNR, anisotropy sparsity has less blurring and can better maintain the detailed structures.Acknowledgements
No acknowledgement found.References
[1] Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 2013;72:41–47.
[2] Truong TK, Guidon A. High-resolution multishot spiral diffusion tensor imaging with inherent correction of motion-induced phase errors. Magn Reson Med 2014;71:790–796.
[3] Guo H, Ma X, Zhang Z, Zhang B, Yuan C, Huang F. POCS-enhanced inherent correction of motion-induced phase errors (POCS-ICE) for high-resolution multishot diffusion MRI. Magn Reson Med 2016;75:169–180.
[4] Shi X, Ma X, Wu W, Huang F, Yuan C, Guo H. Parallel imaging and compressed sensing combined framework for accelerating high- resolution diffusion tensor imaging using inter-image correlation. Magn Reson Med 2015;73:1775–1785.
[5] Haldar JP, Wedeen VJ., Nezamzadeh M, Dai G, Weiner MW, Schuff N, Liang ZP. Improved diffusion imaging through SNR-enhancing joint reconstruction. Magn Reson Med 2013;69:277–289.
[6] Jiang H, van Zijl PC, Kim J, Pearlson GD, Mori S. DtiStudio: resource program for diffusion tensor computation and fiber bundle tracking. Comput Methods Programs Biomed 2006;81:106–116.
Figures