3332
Joint Non-local Means Reconstruction for Correction of Phase-Induced Errors in Diffusion Tensor Imaging1Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Ankara, Turkey
Synopsis
Multiple acquisitions have to be averaged to achieve reasonable signal-to-noise ratio (SNR) in high-resolution diffusion tensor imaging (DTI). However, involuntary global/local motions during diffusion-sensitizing gradients create k-space shifts, and global/local phase differences between different acquisitions, complicating image reconstruction. In this work, we propose a phase-correcting joint non-local means reconstruction that effectively prevents phase cancellations and reduces noise. This technique jointly utilizes the images from different diffusion-encoding directions to preserve the fractional anisotropy (FA) map. Results are demonstrated for in vivo spinal cord DTI and on a simulated DTI dataset.
Introduction
Diffusion tensor imaging (DTI) has a relatively low signal-to-noise ratio (SNR) due to diffusion-induced signal decay. Thus, multiple acquisitions have to be averaged to obtain a reasonable SNR, especially for high-resolution imaging. However, involuntary motion during diffusion-sensitizing gradients creates k-space shifts, and global/local phase differences between image averages 1. Here, we propose a phase-correcting joint non-local means reconstruction that effectively prevents phase cancellations and reduces noise. This technique jointly utilizes the images from different diffusion-encoding directions to preserve the fractional anisotropy (FA) map.Methods
In vivo DTI Experiments: In vivo DTI images of the cervical spinal cord were acquired in the sagittal plane, on a 3T GE MR 750 scanner using 8-channel CTL coil. The field-of-view (FOV) in the phase-encode direction was reduced using a 2D RF excitation 2-5. DTI images with 12 directions at b = 500 s/mm2 were acquired, with two T2-weighted images. Other parameters were: 1x1 mm2 in-plane resolution, FOV = 20x5 cm2, 3 mm slice thickness, TE = 52 ms, TR = 4600 ms, 17-minute total scan time, 16 image averages (NEX), 62.5% partial k-space coverage. The phase issues were present near nerve roots, particularly when the diffusion-encoding direction was in the A/P direction. This indicates a motion of the cord in the A/P direction, which is consistent with the literature on nerve root pulsations synchronized to heart and CSF pulsations 6-8.
DTI Simulations: For quantitative assessment, a simulated DTI set for spinal cord was generated. First, a T2-weighted spinal cord image was segmented using PropSeg Spinal Cord Segmentation Toolbox 9, 10. DTI images were generated with 12 directions at b = 500 s/mm2 using the diffusion coefficients in 11, with NEX = 16. To model the rigid body motion, random global linear phases were added to each NEX. A small region was selected on the spinal cord to add Gaussian-shaped local phase, assuming a random motion level in the A/P direction 1, 8. Finally, complex noise was added in k-space.
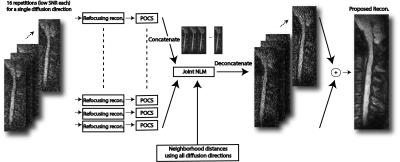
Proposed Reconstruction: The overall image reconstruction is summarized in Fig. 1. Global phase of each diffusion-weighted image was corrected via refocusing reconstruction 12, followed by a POCS partial k-space reconstruction. The resultant images were then processed with a Non-Local-Means (NLM) filter 13,14, which we modified and named “joint NLM” here. Accordingly, all complex-valued NEXs were concatenated in 2D. The images from different diffusion-encoding directions were then concatenated along the third dimension. The joint NLM filter searched for similar neighborhoods, in the resultant 3D matrix. The pixel intensity after filtering was determined by averaging central pixels of similar neighborhoods:
$$m_{NL} (x_i,y_i )=∑_jw(x_i,y_i ; x_j,y_j )m(x_j,y_j ) \quad (1)$$ To find the weight $$$ w(x_i,y_i ; x_j,y_j ) $$$, the joint Euclidean distance between the neighborhoods were calculated by considering all 12 diffusion-encoding directions. This important step helps preserve the integrity of the FA map.
$$w(x_i,y_i ; x_j,y_j )=\frac{1}{Z_i} e^{\frac{-|m(N(x_i,y_i,z))-m(N(x_j,y_j,z)|^2}{h^2} } \quad (2)$$ Here, $$${Z_i}$$$ is a normalization constant, and the smoothing parameter $$${h}$$$ was determined by:
$$h^2=2β|N_i | \sum_{k=1}^{N_\text{diff dir}} \sigma_k \quad (3)$$ The standard deviations $$$ \sigma_k $$$ were computed directly from the images, and $$$\beta$$$ was set to 0.5 14. This entire procedure was repeated for each direction, using the joint Euclidian distance. For comparison, two additional image reconstructions were implemented. For both cases, refocusing reconstruction and partial k-space reconstruction were first performed, as in the proposed reconstruction. Then, (1) the absolute value average and (2) complex value average of NEXs were computed.
Results and Discussion
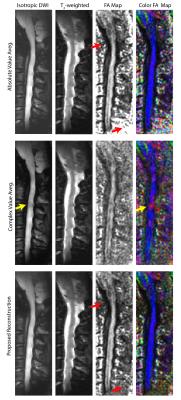
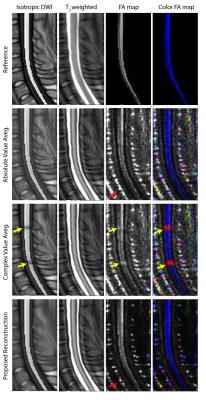
Figure 2 displays the in vivo imaging results in the spinal cord. Absolute value averaging causes a noise accumulation in the background. Complex averaging results in local phase problems that are especially prominent in the FA map, as diffusion-direction dependent phase cancellations lead to incorrect estimation of the principle diffusion direction. Proposed reconstruction not only suppresses the noise in the background (red arrows), but also overcomes the local phase issues. DTI simulation results with reference (ground-truth) images are displayed in Fig. 3. Again, the proposed reconstruction overcomes the local phase problems while reducing the noise in the background of the FA maps. For a quantitative assessment, the Euclidean distance between the principle eigenvectors of the reference data and each method were computed. The histograms of these differences (Fig. 4) reveal that the proposed reconstruction yields the closest match to the reference FA map.Conclusion
We proposed a phase-correcting non-local means image reconstruction that overcomes local phase-cancellation problems, while preserving the integrity of the FA maps. The results are demonstrated with in vivo and simulated spinal cord DTI, with improvements in both image quality and FA metrics.Acknowledgements
This work was supported by the European Commission through an FP7 Marie Curie Career Integration Grant (PCIG13-GA-2013-618834), by the Turkish Academy of Sciences through TUBA-GEBIP 2015 program, and by the BAGEP Award of the Science Academy.References
1. A. Anderson and J. Gore, "Analysis and correction of motion artifacts in diffusion weighted imaging," Magnetic Resonance in Medicine, no. 32, p. 379–387, 1994
2. EU. Saritas, C. Cunningham, J. Lee, E. Han and D. Nishimura, "DWI of the spinal cord with reduced FOV single-shot EPI," Magnetic Resonance in Medicine, no. 60, p. 468–473, 2008.
3. G. Zaharchuk, EU. Saritas, J. Andre, C. Chin, J. Rosenberg, T. Brosnan, A. Shankaranarayanan, D. Nishimura and N. Fischbein, "Reduced field-of-view diffusion imaging of the human spinal cord: comparison with conventional single-shot echo-planar imaging," Am J Neuroradiol, no. 32, p. 813–820, 2011
4. J. Andre, EU. Saritas, G. Zaharchuk, J. Rosenberg, S. Komakula, S. Banerjee, A. Shankaranarayanan, D. Nishimura and N. Fischbein, "Clinical evaluation of reduced field-of-view diffusion-weighted imaging of the cervical and thoracic spine and spinal cord," Am J Neuroradiol, no. 33, p. 1860–1866, 2012.
5. EU. Saritas, D. Lee, T. Cukur, A. Shankaranarayanan and D. Nishimura, "Hadamard Slice Encoding for Reduced-FOV Diffusion-Weighted Imaging," Magnetic Resonance in Medicine, no. 72, pp. 1277-1290, 2014
6. Figley, C. R., and P. W. Stroman. "Investigation of human cervical and upper thoracic spinal cord motion: implications for imaging spinal cord structure and function." Magnetic resonance in medicine 58.1 (2007): 185-189.
7. Matsuzaki, H., et al. "The origin and significance of spinal cord pulsation." Spinal Cord 34.7 (1996): 422-426.
8. Winklhofer, S., et al. "Spinal cord motion: influence of respiration and cardiac cycle." RöFo-Fortschritte auf dem Gebiet der Röntgenstrahlen und der bildgebenden Verfahren. Vol. 186. No. 11. © Georg Thieme Verlag KG, 2014.
9. Fonov, V. S., et al. "Framework for integrated MRI average of the spinal cord white and gray matter: The MNI–Poly–AMU template." Neuroimage 102 (2014): 817-827
10. De Leener, Benjamin, Julien Cohen-Adad, and Samuel Kadoury. "Automatic segmentation of the spinal cord and spinal canal coupled with vertebral labeling." IEEE transactions on medical imaging 34.8 (2015): 1705-1718.
11. Helenius, Johanna, et al. "Diffusion-weighted MR imaging in normal human brains in various age groups." American journal of neuroradiology 23.2 (2002): 194-199.
12. Miller, Karla L., and John M. Pauly. "Nonlinear phase correction for navigated diffusion imaging." Magnetic resonance in medicine 50.2 (2003): 343-353.
13. A. Buades, B. Coll and J. M. Morel, "A review of image denoising algorithms, with a new one," Multiscale Modeling & Simulation, vol. 4, no. 2, pp. 490-530, 2005.
14. P. Coupe, P. Yger, S. Prima, P. Hellier and C. Kervrann, "An optimized blockwise nonlocal means denoising Filter for 3-D magnetic resonance images," IEEE Transactions on Medical Imaging, vol. 4, no. 27, pp. 425-41, 2008.
Figures