3226
On Partial Fourier Acquisition in 4D Flow MRI of Mean Velocities and Turbulent Kinetic Energy1ETH Zurich, Zurich, Switzerland
Synopsis
Scan time reduction with partial Fourier was investigated for 4D flow MRI of mean velocity and turbulent kinetic energy. It was shown analytically, that PF leads to a loss in resolution for phase images. According to experiments with in-vivo data, the precondition of slowly varying phases is not met for PF reconstructions of 4D flow MRI, making homodyne reconstruction and POCS fail. Therefore, it is concluded, that PF cannot recover missing k-space samples in 4D flow MRI and does not offer a benefit over symmetric k-space sampling with the same number of phase encodes.
Purpose
4D Flow MRI is associated with long scan times. Partial Fourier (PF) acquisition [1] is a standard method to shorten scan times in MR imaging. It is listed as an option to reduce scan durations in 4D Flow MRI [2]. Various reconstruction approaches exist to repopulate missing data in k-space [3], [4], [5]. However, all these approaches assume or approximate Hermitian symmetry, a condition not met in phase-contrast flow imaging. The objective of the present work is to revisit Partial Fourier acquisition for flow-sensitized imaging approaches and assess its limitations for 4D Flow MRI of mean velocity [6] and Turbulent Kinetic Energy (TKE) [7].Theory
The Fourier transform of a real-valued object signal exhibits Hermitian symmetry, i.e. $$$ S(k) = S^*(-k)$$$. Theoretically, one half of k-space would be sufficient to reconstruct the image. Although MR object signals are not real-valued, the low-frequency object phase $$$\phi_l(x)$$$ can serve as an estimate of the phase of the image. This allows to unwind the phase and to enforce Hermitian symmetry for $$$I(x)e^{i\phi_l(x)}$$$. To obtain $$$\phi_l(x)$$$, the lower frequencies must be acquired symmetrically. The ratio of acquired data to total k-space data is referred to as PF fraction [8].
Given a real-valued image, in homodyne reconstruction (HR) [3] the inverse Fourier is formulated as
$$I(x)=\int_{-k_{max}}^{-k_{0}} s(k) e^{ikx} dk+\int_{-k_0}^{k_0} s(k) e^{ikx} dk+\int_{k_0}^{{k_{max}}} s(k) e^{ikx} dk = \int_{-k_0}^{k_0} s(k) e^{ikx} dk+2 \int_{k_0}^{k_{max}} s(k) e^{ikx} dk$$
where Hermitian symmetry is exploited in order to write $$$\int_{-k_{max}}^{-k_{0}} s(k) e^{ikx} dk = \left[\int_{k_{max}}^{k_{0}} s(k') e^{ik'x} dk'\right ]^*$$$.
Hermitian symmetry is exploited in iterative algorithms. A projection onto convex sets (POCS) [4] algorithm alternates between projections onto the set of real-valued images and projections onto the set of data which match the acquired k-space data and converges to a solution which lies in both sets.
Methods
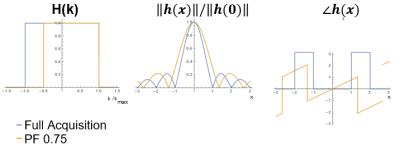
PF sampling is modeled as a multiplication of k-space with a shifted rectangular window. For a given PF fraction, the corresponding point spread function becomes a sinc-function with a phase modulation which depends on the PF fraction.
$$H(k) = \Pi_{2k_{max}PF}(k-(1-PF)k_{max}) \xrightarrow{\mathscr{F}^{-1}} e^{i2\pi(1-PF)k_{max}x}k_{max}\frac{sin(2\pi k_{max}PFx)}{2\pi k_{max}PFx}$$
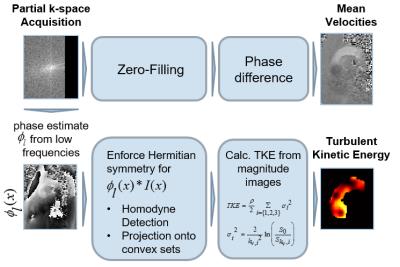
4D Flow data in the aortic arch of a healthy volunteer were acquired on a 3T Philips Ingenia system (Philips Healthcare, Best, the Netherlands) using a navigated Cartesian four-point phase-contrast gradient-echo sequence with uniform venc of 200 cm/s and spatial resolution of 1.83x1.83x1.83 mm3. The data were retrospectively undersampled to simulate PF acquisition with a PF fraction of 0.75 along the in-plane phase encode dimension. Data were reconstructed using HR, POCS, and zero-filling. The reconstruction procedure is outlined in Figure 2. Pixel velocities and pixel TKE were derived [7] and root mean square errors relative to the fully sampled reference computed. To assess the effect which the varying image phase has on magnitude reconstruction, the phase of the image was set to zero before reconstructing k-space and compared to the reconstruction of the velocity-encoded image.
Results
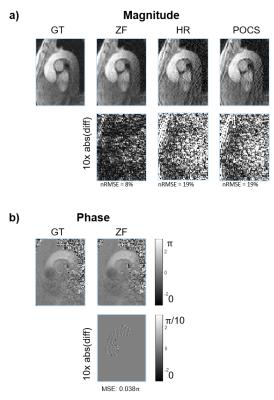
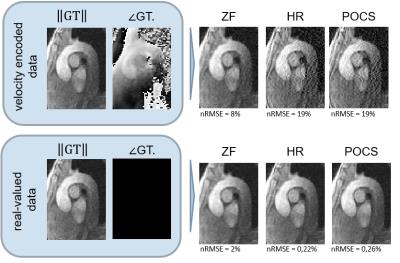
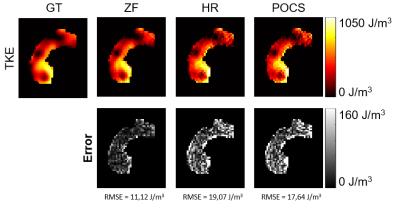
HR and POCS reconstruction of magnitude images show increased noise levels. ZF does not increase noise, but blurs the image (Figure 3). The effects of PF on complex-valued images are shown in Figure 4. While for real-valued data, POCS and homodyne detection work well, they increase noise for the complex-valued images and the best result in the latter case is obtained with zero-filling. The calculated TKE values are least noisy for ZF (Figure 5).Discussion
Without further processing PF acquisitions reduce spatial resolution corresponding to the inverse of the bandwidth covered in k-space. The asymmetric k-space sampling causes a linear phase in the image which is removed by the phase-difference operation. Reconstruction algorithms to “recover” spatial resolution in the magnitude images are compromised by the spatial distribution in the image phase. To this end, the assumption of low frequency phase changes as required by Partial Fourier reconstruction algorithms is no longer valid and introduces distortions in the magnitude images and TKE data. Accordingly, it is concluded that PF acquisition in 4D Flow MRI does not offer a benefit over symmetric k-space sampling with the same number of phase encodes. Potential paths to address the resolution loss due to PF acquisition include the incorporation of prior knowledge on velocity field properties in constrained iterative image reconstruction [5], [9], [10].Acknowledgements
No acknowledgement found.References
[1] G. McGibney, M. R. Smith, S. T. Nichols, and a Crawley, “Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI.,” Magn. Reson. Med., vol. 30, no. 1, pp. 51–59, 1993.
[2] P. Dyverfeldt, M. Bissell, A. J. Barker, A. F. Bolger, C.-J. Carlhäll, T. Ebbers, C. J. Francios, A. Frydrychowicz, J. Geiger, D. Giese, and others, “4D flow cardiovascular magnetic resonance consensus statement,” J. Cardiovasc. Magn. Reson., vol. 17, no. 1, p. 1, 2015.
[3] D. C. Noll, D. G. Nishimura, and A. Macovski, “Homodyne Detection in Magnetic Resonance Imaging,” IEEE Trans. Med. Imaging, vol. 10, no. 2, pp. 154–163, 1991.
[4] J. Cuppen and A. van Est, “Reducing MR imaging time by one-sided reconstruction,” Magn. Reson. Imaging, vol. 5, no. 6, pp. 526–527, Nov. 1987.
[5] T. Kuestner, C. Wurslin, S. Gatidis, P. Martirosian, K. Nikolaou, N. Schwenzer, F. Schick, B. Yang, and H. Schmidt, “MR image reconstruction using a combination of Compressed Sensing and partial Fourier acquisition: ESPReSSo,” IEEE Trans. Med. Imaging, vol. 62, no. c, pp. 1–1, 2016. [6] M. Markl, A. Frydrychowicz, S. Kozerke, M. Hope, and O. Wieben, “4D flow MRI,” J. Magn. Reson. Imaging, vol. 36, no. 5, pp. 1015–1036, 2012.
[7] P. Dyverfeldt, J. P. E. Kvitting, A. Sigfridsson, J. Engvall, A. F. Bolger, and T. Ebbers, “Assessment of fluctuating velocities in disturbed cardiovascular blood flow: In vivo feasibility of generalized phase-contrast MRI,” J. Magn. Reson. Imaging, vol. 28, no. 3, pp. 655–663, 2008.
[8] M. A. Bernstein, K. F. King, and X. J. Zhou, Handbook of MRI pulse sequences. Elsevier, 2004.
[9] G. Li, J. Hennig, E. Raithel, M. Büchert, D. Paul, J. G. Korvink, and M. Zaitsev, “An L1-norm phase constraint for half-Fourier compressed sensing in 3D MR imaging,” MAGMA, vol. 28, no. 5, pp. 459–472, 2015.
[10] C. Santelli, M. Loecher, J. Busch, O. Wieben, T. Schaeffter, and S. Kozerke, “Accelerating 4D Flow MRI by Exploiting Vector Field Divergence Regularization.”
Figures