3221
Bootstrapped Estimates of Velocity Uncertainty for 4D Flow PC-MRI1Department of Radiological Sciences, University of California, Los Angeles, CA, United States
Synopsis
We implement and analyze a bootstrapping method to estimate VNR measurements with a limited number of 4D Flow acquisitions. Bootstrapped estimates were created from sets of 2 acquisitions and sets of 5 acquisitions. The VNR maps were compared to a ground truth VNR measurement generated from 50 acquisitions in a flow phantom. The method was also demonstrated in vivo to generate VNR maps of the carotid arteries.
Introduction
Determining the accuracy and precision of 4D Flow images is not straightforward, but is very important for improving the clinical acceptance of this technique. Characterizing the uncertainty of these measurements can also help in developing and comparing acquisition and reconstruction strategies, as well as improve post-processing and visualization techniques such as probabilistic streamlines [1]. Velocity to noise ratios (VNR) are an important measurement of precision. VNR measurements may be acquired with ROI based methods, however this averages and therefore obscures the distribution of VNR within any given vessel. To capture the spatial dynamics of uncertainty, a voxel-wise method would be preferable, but this usually requires many measurements that could take prohibitively long with standard 4D Flow acquisitions.
Bootstrapping is a method of quantifying measurement uncertainty that is used extensively by the diffusion tensor imaging (DTI) community [2,3] that allows for the quantification of uncertainty with far fewer measurements. These error estimation methods can easily be applied to 4D Flow acquisitions that employ multi-directional balanced encoding, but currently they have not been reported in the literature. The objective of this work was to implement and analyze a bootstrapping method to estimate VNR measurements with a limited number of 4D Flow acquisitions.
Methods
For phantom experiments, a flow pump (CardioFlow 5000 MR, Shelly Medical) pumped blood-mimicking fluid at a constant flow rate of 70 mL/s for the duration of the scanning (1.5 hours). 50 back-to-back 3D PC-MRI scans were acquired using a stack-of-stars trajectory, 1mmx1mmx2mm resolution, 256x256x32mm FOV, 1:40 minutes scan time per volume. The data was acquired with a 5pt balanced encoding scheme [4] with Venc=120 cm/s. For in vivo data, a similar sequence was repeated three times in the neck of healthy volunteer with Venc=80 cm/s.
To account for possible phase drift in the data, eddy current corrections were applied individually to all data using 2nd order polynomial fitting to stationary tissue, as well as correcting for intensity drifts in the data.
Phantoms: The baseline VNR measure was calculated as the voxel-wise mean divided by the standard deviation over all 50 samples and was designated $$$VNR_{mult50}$$$. Similarly, VNR was calculated as mean over standard deviation using only 5 subsequent acquisitions and is designated $$$VNR_{mult5}$$$. Bootstrapped VNR measurements were calculated by selecting all combinations of velocity encodes with replacement from two or five subsequent scans (for a total of 32 or 3125 bootstrapped datasets) and were designated $$$VNR_{boot2}$$$ and $$$VNR_{boot5}$$$. Vessel-wide ROI based measures of VNR were also estimated from the subtraction of two subsequent datasets designated as $$$VNR_{diff}$$$ [5] for comparison. Vessel-wide ROI VNR measurements were repeated 30 times by resampling from the group of 50.
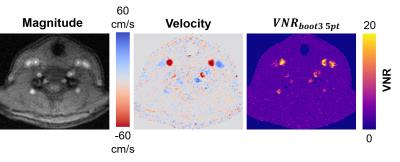
Human Subject: VNR maps were calculated using the bootstrapping method from 3 acquisitions.
Results
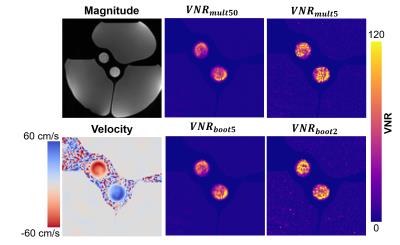
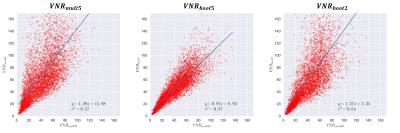
Figure 1 shows the voxel-wise bootstrapped VNR maps. The VNR is higher in the bootstrapped estimates, but the spatial pattern of VNR within the vessel matches up well, especially for the $$$VNR_{boot5}$$$ method. Figure 2 shows the voxel-wise comparison between $$$VNR_{mult50}$$$ and the other VNR estimates. Figure 3 shows vessel-wide VNR ROI measurements across the two separate phantom vessels. Figure 4 shows an in vivo example of the technique in the carotid arteries.Discussion
This study introduces the use of bootstrapping methods for estimating VNR on a voxel-wise basis. Good depictions of VNR and spatial distributions are seen within vessels, demonstrating that this technique could be a useful tool for characterizing error in 4D-Flow. When compared to a conventional calculation of VNR over 5 acquisitions, bootstrapping gave estimates that were much closer to the 50 acquisition ‘truth’ estimate. The bootstrapping method could be particularly useful for testing and comparing the effectiveness of acquisition, reconstruction, or postprocessing methods.
When spatial maps of VNR are not required, the ROI based subtraction technique is superior to bootstrapping as it requires only two acquisitions and provides reliable results comparable to bootstrapping with 5 acquisitions.
Acquiring five acquisitions in vivo is generally impractical, so the effectiveness of bootstrapping with only two back-to-back measurements is important. Bootstrapping with a low number of samples is known to underestimate the standard error [3], which was clearly seen in this study. This problem has been addressed in the DTI field using more advanced model-based bootstrap methods [3,6] that could help give more accurate measure with only two scans.
Ultimately, this study shows that bootstrapped estimates of VNR are a potentially useful tool for making voxel-wise VNR maps with a small number of extra acquisitions to better understand the errors in 4D Flow imaging.
Acknowledgements
Funding support from the Department of Radiological Sciences and Siemens Medical Solutions.References
[1] Friman, O., Hennemuth, A., Harloff, A., Bock, J., Markl, M. and Peitgen, H.O., 2011. Probabilistic 4D blood flow tracking and uncertainty estimation. Medical image analysis, 15(5), pp.720-728.
[2] Heim, S., Hahn, K., Sämann, P.G., Fahrmeir, L. and Auer, D.P., 2004. Assessing DTI data quality using bootstrap analysis. Magnetic resonance in Medicine, 52(3), pp.582-589.
[3] Chung, S., Lu, Y. and Henry, R.G., 2006. Comparison of bootstrap approaches for estimation of uncertainties of DTI parameters. NeuroImage, 33(2), pp.531-541.
[4] Johnson, K.M. and Markl, M., 2010. Improved SNR in phase contrast velocimetry with five-point balanced flow encoding. Magnetic resonance in medicine, 63(2), pp.349-355.
[5] Dietrich, O., Raya, J.G., Reeder, S.B., Reiser, M.F. and Schoenberg, S.O., 2007. Measurement of signal-to-noise ratios in MR images: Influence of multichannel coils, parallel imaging, and reconstruction filters. Journal of Magnetic Resonance Imaging, 26(2), pp.375-385.
[6] Whitcher, B., Tuch, D.S., Wisco, J.J., Sorensen, A.G. and Wang, L., 2008. Using the wild bootstrap to quantify uncertainty in diffusion tensor imaging. Human brain mapping, 29(3), pp.346-362.
Figures