3137

Improved Golden-Angle Stack-of-Stars Non-Contrast Enhanced 4D Dynamic MR Angiography using Parallel Imaging and Compressed Sensing
Ziwu Zhou1, Fei Han1, Songlin Yu2, Dandan Yu2, Stanislas Rapacchi1, Danny J.J. Wang3, Lirong Yan3, and Peng Hu1

1Radiological Sciences, University of California, Los Angeles, Los Angeles, CA, United States, 2Neurology, University of California, Los Angeles, Los Angeles, CA, United States, 3Neurology, University of Southern California, Los Angeles, CA, United States

Synopsis

In this study, we investigated the feasibility of accelerating a recently proposed arterial spin labeling (ASL) based, time-resolved non-contrast enhanced dynamic MR angiography (NCE-dMRA) technique using parallel imaging and compressed sensing. By taking advantage of the inherent and unique “subtraction sparsity” in ASL type acquisition, we combined a recently developed CS technique, which uses a magnitude subtraction to enhance sparsity in MRA data, with the ESPIRiT method for SENSE type PI reconstruction. Proposed method was compared with the previously used KWIC reconstruction to demonstrate its advantage in reducing temporal blurring caused by view-sharing.

Introduction

The detailed characterization of flow hemodynamics is of great importance for clinical diagnosis and treatment of various cerebrovascular disorders. Recently, an arterial spin labeling (ASL) based, time-resolved, non-contrast enhanced dynamic MR angiography (NCE-dMRA) technique has been developed1 to capture the flow passage within cerebrovascular system. By using a golden-angle stack-of-stars (SOS) sampling scheme2 and k-space weighted image contrast (KWIC) reconstruction3, it offers an apparent temporal frame rate of 100ms and a spatial resolution of 1mm3. However, due to the view-sharing in KWIC reconstruction, mild temporal blurring sometimes potentially occurs in small vessels with fast flow, especially at the first and last few frames due to the asymmetry of KWIC filter. Parallel imaging (PI) and compressed sensing (CS) combined reconstruction has recently emerged as a promising approach to accelerate data acquisition in dynamic MRI4,5. The implementation of PI+CS, however, remains challenging in ASL imaging due to the intrinsic low SNR. In this work, we aimed to investigate the feasibility of applying PI+CS combined reconstruction in ASL-based NCE-dMRA, by taking advantage of the inherent and unique “subtraction sparsity” in ASL type acquisition.

Methods

Proposed Reconstruction: Figure 1a shows an example of the k-space of two temporal frames after KWIC filtering. To reduce the view-sharing introduced in the outer k-space region, we evaluated an alternative approach wherein the entire k-space only consists of radial spokes with number equal to that in the central k-space region of KWIC filtered k-space (Figure 1b). Resulting highly under-sampled k-space was reconstructed with following algorithm that combines a recently developed CS technique6,7 with the ESPIRiT method8 for SENSE type PI reconstruction (called PI+CS w/ Magnitude Subtraction): $$(m_1,m_2)=argmin\left(\begin{array}{c}\sum_{i=1}^N||NUFFT(S_im_1)-y^i_1||^2+\lambda||Wm_1||_1+\mu||MAG(m_1)-MAG(m_2)||_1\\ \sum_{i=1}^N||NUFFT(S_im_2)-y^i_2||^2+\lambda||Wm_2||_1+\mu||MAG(m_1)-MAG(m_2)||_1\end{array}\right),$$

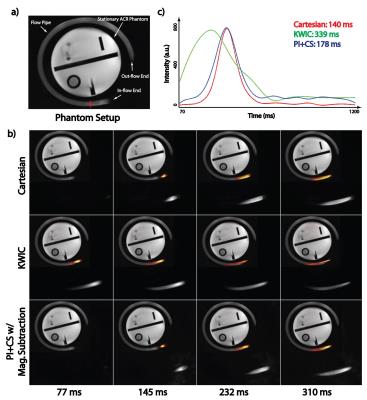
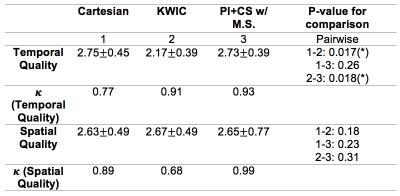
where $$$y^i_1$$$ and $$$y^i_2$$$ are under-sampled k-space data ($$$i^{th}$$$ coil) for label and control acquisitions; $$$m_1$$$ and $$$m_2$$$ are corresponding images to be recovered; $$$NUFFF(.)$$$ is the non-uniform fast Fourier transform (9); $$$S_i$$$ is the $$$i^{th}$$$ sensitivity map; $$$N$$$ is the total number of coils; $$$W$$$ is the Daubechies spatial wavelets; $$$MAG(.)$$$ is the magnitude operator, and $$$\lambda$$$ and $$$\mu$$$ are regularization parameters. Optimization problem was solved with ADMM algorithm (10) implemented in BART (11). Phantom Experiment: To demonstrate the effect of view-sharing on NCE-dMRA with fast flow, a phantom experiment was performed. A medium-sized flow pipe with constant flow waveform (50cm/s) was circled around a stationary phantom (Figure 2a). The 3D SOS NCE-dMRA sequence and a reference Cartesian NCE-dMRA sequence (12) were used to image the phantom. 16 frames were acquired in Cartesian sequence and 320 spokes/slice were acquired in 3D SOS sequence. The 3D SOS dataset was then retrospectively reconstructed with KWIC (20 spokes/slice at central region, 5 rings with a total of 160 spokes/slice for each frame) and proposed method (20 spokes/slice/frame), both generated 16 frames in total. Other imaging protocol includes: TR = 4.85 ms, TE = TR/2, FA = 25, BW = 849Hz/ pixel, spatial resolution: 1x1x1 mm3, TA = 156s for Cartesian sequence and 71s for 3D SOS sequence. In-vivo Experiment: 6 volunteers were scanned using the same sequences and similar protocols. Similar retrospective reconstructions were carried out for the 3D SOS data. Image Evaluation: The quality of three reconstructions were graded by two readers according to a 3-point scale (1-3, non-diagnostic to excellent) in terms of spatial and temporal quality. Weighted kappa coefficient was calculated to evaluate inter-observer agreement. Wilcoxon signed-rank test were conducted pairwise to compare the selected pairs of reconstructions in terms of subjective scores.

Results

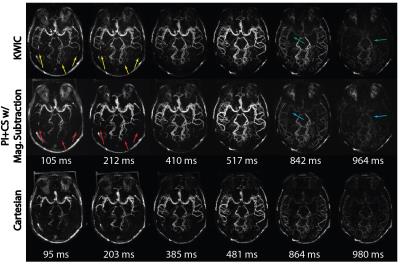
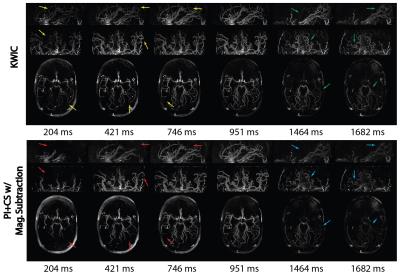
Figure 2 illustrates the impact of view-sharing in the phantom experiment. Improved visualization of flow dynamics at the first four frames can be seen in the proposed method. Figure 3 shows the reconstructed MIP images of a volunteer. Proposed method provides clearer delineation of signal evolution from medium- to small-size vessel branches. Figure 4 displays six frames of MIP images in sagittal, coronal, and axial views. One can also appreciate the temporal blurring effects in small vessels in KWIC images in the first and last few frames compared to the proposed method. Table 1 summarizes subjective scores and weighted kappa coefficient.

Conclusion

By taking advantage of “subtraction sparsity” of the ASL images, a combined CS and PI strategy has been proposed and successfully implemented in golden-angle stack-of-stars NCE-dMRA. Compared to the previous KWIC method, the proposed strategy allows better depiction of flow dynamics of small vessels at early and late frames.

Acknowledgements

This research was supported by AHA 16SDG29630013, NIH R01EB014922, UH2NS100614, and NIH R01HL127153.

References

1. Song HK, Yan L, Smith RX, Xue Y, Rapacchi S, Srinivasan S, Ennis DB, Hu P, Pouratian N, Wang DJJ. Noncontrast enhanced four dimensional dynamic MRA with golden angle radial acquisition and K-space weighted image contrast (KWIC) reconstruction. Magn Reson Med. 2014; 72: 1541–1551.

2. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging 2007;26:68–76.

3. Song HK, Dougherty L. Dynamic MRI with projection reconstruction and KWIC processing for simultaneous high spatial and temporal resolution. Magn Reson Med 2004;52:815–824.

4. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58: 1182–1195.

5. Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magn Reson Med 2008;59:365–373.

6. Rapacchi S, Han F, Natsuaki Y, Kroeker R, Plotnik A, Lehrman E, Sayre J, Laub G, Finn JP, Hu P. High spatial and temporal resolution dynamic contrast-enhanced magnetic resonance angiography using compressed sensing with magnitude image subtraction. Magn Reson Med 2014;71:1771–1783.

7. Rapacchi S, Natsuaki Y, Plotnik A, Gabriel S, Laub G, Finn JP, Hu P. Reducing view-sharing using compressed sensing in time-resolved contrast-enhanced magnetic resonance angiography. Magn Reson Med 2014;74:474–481.

8. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990–1001.

9. Fessler JA. On NUFFT-based gridding for non-Cartesian MRI. J MagnReson 2007;188:191–195.

10. Boyd S. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn2010;3:1–122.

11. BART: version 0.2.04 (2014) DOI: 10.5281/zenodo.12495.

12. Yan L, Wang S, Zhuo Y, Wolf RL, Stiefel MF, An J, Ye Y, Zhang Q, Melhem ER, Wang DJ. Unenhanced dynamic MR angiography: high spatial and temporal resolution by using true FISP-based spin tagging with alternating radiofrequency. Radiology 2010;256:270–279.

Figures

Figure 1. a): Illustration of KWIC k-space filtering technique. K-space is divided into 3 regions, with 5 views in the central region, 8 views in the middle region, and a total of 13 views in the outer region. The temporal footprint of reconstructed frames is calculated as the acquisition time of all 13 views, although temporal resolution is only as short as the length of 5 views in this example. b): In the proposed method, each frame only contains 5 views without overlapping. This makes the temporal footprint of reconstructed frames equal to the temporal resolution.

Figure 2. a): Overview of experiment setup. b): First four temporal frames of Cartesian acquisition, KWIC and proposed method. Due to view-sharing, KWIC reconstruction has relative strong temporal blurring at these four frames. The proposed algorithm, however, recovered artifact-free images without any temporal blurring. c): The intensity of signal at red cross point in a) is plotted against time. Full-width half-maximum was calculated as the apparent time it took for the labeled fluid region to pass the selected position.

Figure 3. MIP images of KWIC reconstruction, proposed PI+CS reconstruction with magnitude subtraction and Cartesian reference acquisition at six frames. Temporal blurring effect of KWIC caused early filling (yellow arrows) and late drainage (green arrows) of small vessels, while the proposed PI+CS method provided clean and sharp images with temporal behavior (red and blue arrows) on these vessels comparable to Cartesian acquisition.

Figure 4. MIP images of 3D SOS acquisition along sagittal, coronal and axial views. The temporal blurring effect can be clearly visualized in all three planes in KWIC reconstruction (yellow and green arrows), while the proposed method showed reduced temporal blurring and improved delineation of signal evolution (red and blue arrows).

Table 1. Subjective image quality scores and weighted kappa coefficients κ for temporal/spatial quality and different imaging techniques. P<0.05 was considered statistically significant. (*) denotes statistical significance. PI+CS w M.S.: PI+CS with magnitude subtraction.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3137